转子系统碰磨故障的电机电流特性

杨亚东，杨兆建，杨 波，李 峰

（1.太原理工大学机械工程学院，山西 太原 030024；2.煤矿综采装备山西省重点实验室，山西 太原 030024）

1 引言

转子系统作为旋转机械的重要部件，其发生故障时会对整个设备运行造成影响。针对转子碰磨数学模型的建立与非线性动力学特性的分析，国内外学者已经进行了大量的理论和试验研究，提出了各种故障诊断方法。文献[1]对偏心量变化引起轴向碰磨的弯扭耦合非线性振动特性的改变进行研究，建立了转子静子系统计算模型，使用数值积分法，结合庞加莱映射法进行了数值仿真分析。文献[2]建立了碰磨转子的弯扭耦合数学模型，利用非线性动力学理论对其数学模型动态响应进行仿真。文献[3]考虑轴承油膜力的作用，建立了碰磨转子系统的动力学模型，结合数值仿真对碰磨转子的动力学特性进行研究。文献[4]建立了一个单跨多盘转子系统试验台，轴承为气体静压轴承，实验过程中轴向碰磨与径向碰磨都相继出现并对低频碰磨与工频碰磨现象进行了研究。文献[5]考虑轴向碰磨，径向碰磨以及两种碰磨共同出现的情形，建立了双盘转子系统的有限元连续模型，采用具有回转与剪切效应的梁单元数值模拟了转子系统的动力学特性。文献[6]对转子系统动静碰磨产生的振动信号时频特性分析时，基于二进小波能量谱提取故障特征，故障特征量可以通过对系数和变化最大的能量层进行自功率谱变换而得到。文献[7]建立了单盘转子刚性支承的碰磨非线性弯扭耦合振动微分方程，为碰磨转子系统的故障诊断与优化设计等应用奠定了基础。文献[8]建立Jeffcott 碰磨转子的弯扭耦合振动非线性微分方程，通过数值仿真分析了碰磨故障的扭振时频域特点以及非线性振动特性，重点研究了扭振特性受动静间隙大小的影响。基于单边接触和摩擦条件的有限元理论，文献[9]提出了一种研究转子定子摩擦的新算法，并利用该算法对转子与弹性杆之间的点摩擦进行了实例研究。文献[10]通过利用有约束情况下的拉格朗日运动方程提出一种有效算法来对接触动力学进行建模。该方法不需要直接对接触力物理建模。它可以应用于多点接触情况，并且还能够检测和模拟有害的反向旋转滚动。

可以看出，大多数文献都是通过振动分析方法来对转子系统的碰磨故障进行研究，实际情况下振动传感器安装不便且采集的振动信号易受干扰都会对诊断效果产生影响。以电机的定子电流作为信号分析的出发点，研究其特征与故障发生的相互对应关系，可以弥补其他以直接接触测量信号为主的信号分析方法的不足。存在质量偏心的转子在高速旋转过程中，其不平衡振动位移大于动静间隙时就会发生碰磨故障。故障导致负载转矩发生波动，从而使交流电机的电磁扭矩发生变化，最终电机的定子电流发生变化。在考虑圆盘质量偏心因素的情况下，建立了转子在碰磨条件下的弯扭耦合振动数学模型，基于库伦摩擦力模型求解碰磨力，然后再利用拉格朗日方程推导建立了转子系统碰磨弯扭耦合运动微分方程。以电磁扭矩为纽带，建立转子系统碰磨机电耦合模型，通过仿真来模拟转子系统的碰磨故障并对电流信号进行频谱分析，作为对比验证，同时对振动位移信号进行分析和绘制轴心轨迹图。

2 转子系统碰磨物理模型

以两端刚性支承的单盘转子系统为研究对象，构建转子弯扭耦合模型，计算碰磨力与建立弯扭耦合运动微分方程。转子碰磨模型，如图1 所示。

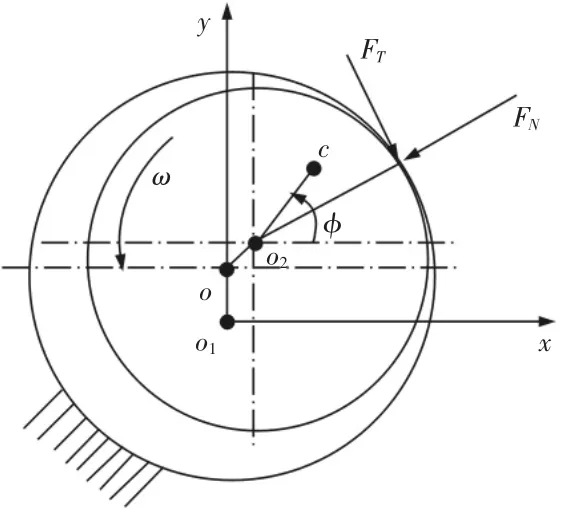
图1 转子碰磨模型Fig.1 Rub-Impact Model of Rotor

图中：m，o—静子形心；o1—转子形心在初始时刻的位置；o2—转子形心；c—转子质心；φ—转角；FN—碰磨径向压力；FT—碰磨切向摩擦力；δ—转子与静子之间的间隙；e—转子的偏心距；μ—转静子接触摩擦系数；J—转动惯量；δ0—转静子形心在初始时刻的不对中量。

2.1 碰磨力的计算

圆盘在旋转过程中，任意时刻转静子的形心距为：

当r＞δ 时，转子和静子发生碰磨，此时在碰磨点处产生相互作用力。假设所研究系统的摩擦满足库伦摩擦定律，则径向压力FN和切向摩擦力FT为：

式中：Ks—定子径向刚度系数，符号Θψ决定摩擦力的方向；ψ—碰磨点的线速度。

式中：R0—碰磨发生点到转子形心的距离，当ψ＜0 时，Θψ=-1，当ψ=0 时，Θψ=0，当 ψ＞0 时，Θψ=1。

将FN、FT分别分解到x 轴和y 轴，则碰磨力为：

2.2 弯扭耦合运动微分方程的建立

将圆盘的运动分解为随质心平动与转动两部分，φ 为圆盘自转角度，当转子匀速平稳旋转时，φ=ωt+θ+φ0，ω 为轴的旋转角速度，θ 为扭振角位移，φ0为初相位。转子系统的动能为：T=TG+TR，TG为圆盘随质心的平动动能，TR为圆盘绕质心的转动动能。

应用第二类拉格朗日方程可导出碰磨转子的弯扭耦合运动微分方程为：

式中：MF—摩擦力矩；MT—转子系统的负载转矩。

3 电机模型

建立三相异步电机在αβO 系统下的仿真模型。

电压方程：

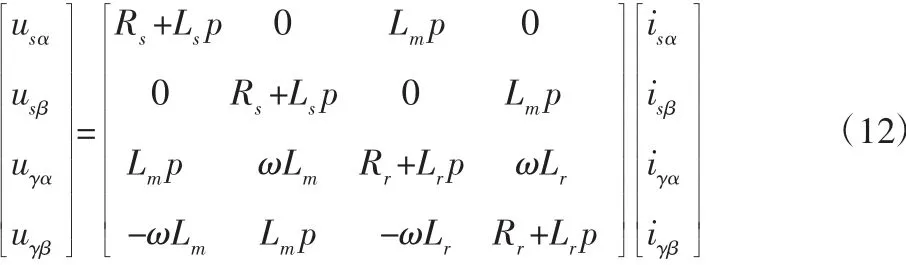
磁链方程：

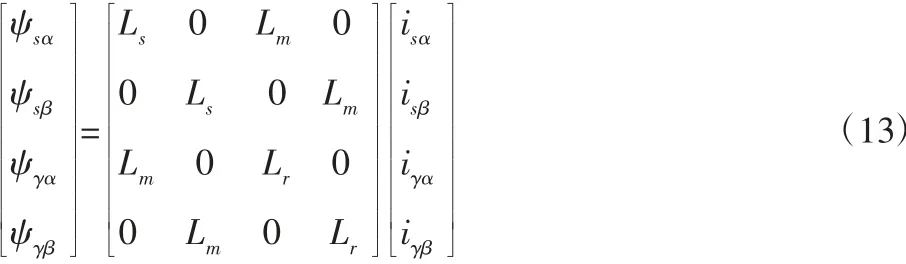
电磁转矩方程：

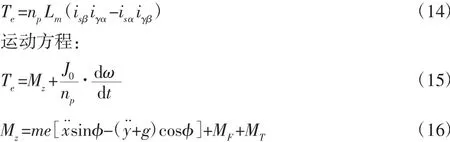
式中：ω—转子转动角速度；

Rs—定子绕组电阻；

Rr—转子绕组电阻；

Ls—定子绕组自感；

Lr—转子绕组自感；

Lm—定转子绕组互感；

np—电极对数；

Te—电磁转矩；

Mz—惯性扭矩与外扭矩之和；

J0—电机的转动惯量。

4 碰磨机电耦合模型的仿真分析

根据式（11）～式（16）建立三相异步电动机—质量偏心转子系统的碰磨机电耦合仿真模型。设定主要仿真参数为：

4.1 偏心距一定时，动静碰磨随转速大小的变化情况

设置偏心距e=0.0008m，在转子系统的转速分别为180r/min、600r/min、900r/min 和1250r/min 时进行仿真得到转子碰磨的定子电流信号与振动位移信号。对定子电流信号进行频谱分析，结合转子振动位移频谱，对特征幅值频率进行观察可以判断碰磨是否发生。同时绘制轴心轨迹图，通过轨迹图形的变形程度来展示碰磨程度的轻重。

当n=180r/min 时，图2 中的电流谱中在50Hz 基频两侧只调制了微弱的转动工频，振动位移谱的特征频率只有工频频率，结合轴心轨迹图为一个光滑椭圆的现象，基本可以判断转子系统在低转速条件运行下，转子运动达不到碰磨条件，碰磨现象没有发生。

当轴转速为600r/min、900r/min 时，如图3、图4 所示，电流谱中的基频两侧在这两种情况下都有转频的倍频成分调制，振动位移谱在工频频率基础上还有明显的2 倍频以及微弱的高倍频谐波成分出现，结合有关碰磨分析理论，可以得出转子系统发生碰磨的结论。由于在碰磨点接触时，转子受到静子的单边冲击约束力，如图5 所示，轴心轨迹出现反弹现象呈内凹状。

转速升高至n=1250r/min 时，对图5 中的电流谱进行观察，基频两侧的特征频率分量调制更加丰富，明显的1/2、3/2 倍频成分同时出现，振动位移频谱中除了对应的频率分量，同时还有微弱的2 倍频、5/2 倍频等高倍频成分。此时转子碰磨程度加重，轴心轨迹多向内凹呈规则的“五角形”形状。

从图2～图5 可以看出，固定偏心距连续升高转速会使转子不平衡运动状态愈加剧烈，轴心轨迹范围愈大造成碰磨程度加重，电流谱与振动位移谱的频率成分更加丰富。

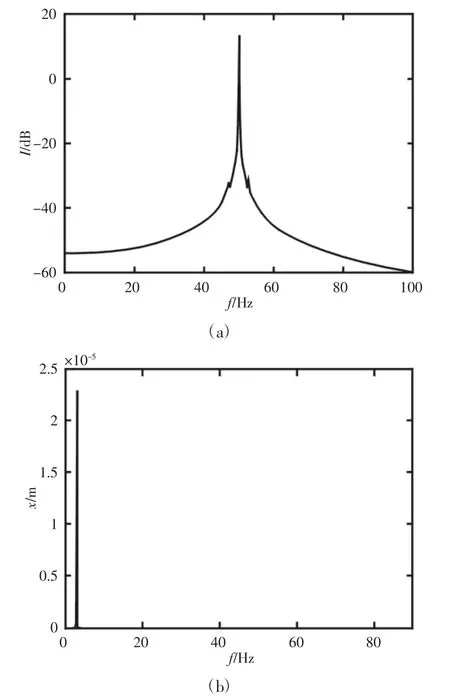
图2 n=180r/min 时，定子电流频谱、振动位移频谱及转子轴心轨迹Fig.2 Stator Current Spectrum，Vibration Displacement Spectrum and Rotor Axis Trajectory in State of n=180r/min

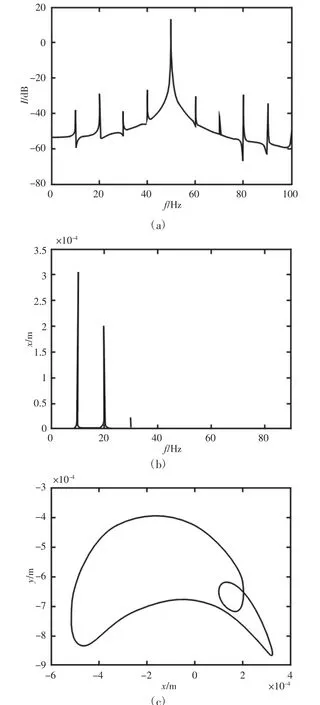
图3 n=600r/min 时，定子电流频谱、振动位移频谱及转子轴心轨迹Fig.3 Stator Current Spectrum，Vibration Displacement Spectrum and Rotor Axis Trajectory in State of n=600r/min

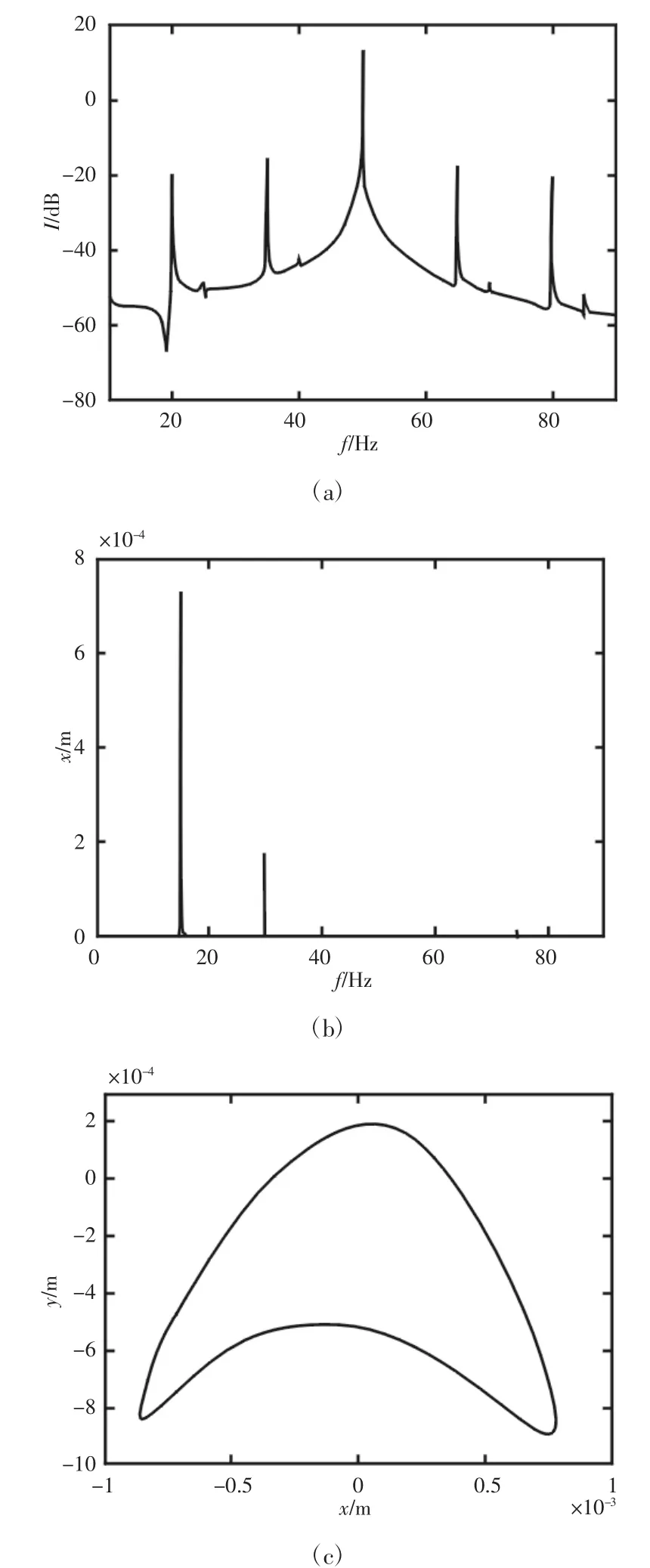
图4 n=900r/min 时，定子电流频谱、振动位移频谱及转子轴心轨迹Fig.4 Stator Current Spectrum，Vibration Displacement Spectrum and Rotor Axis Trajectory in State of n=900r/min

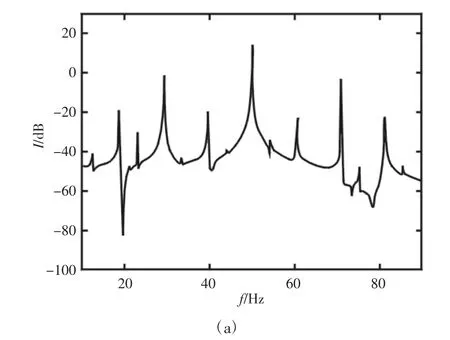
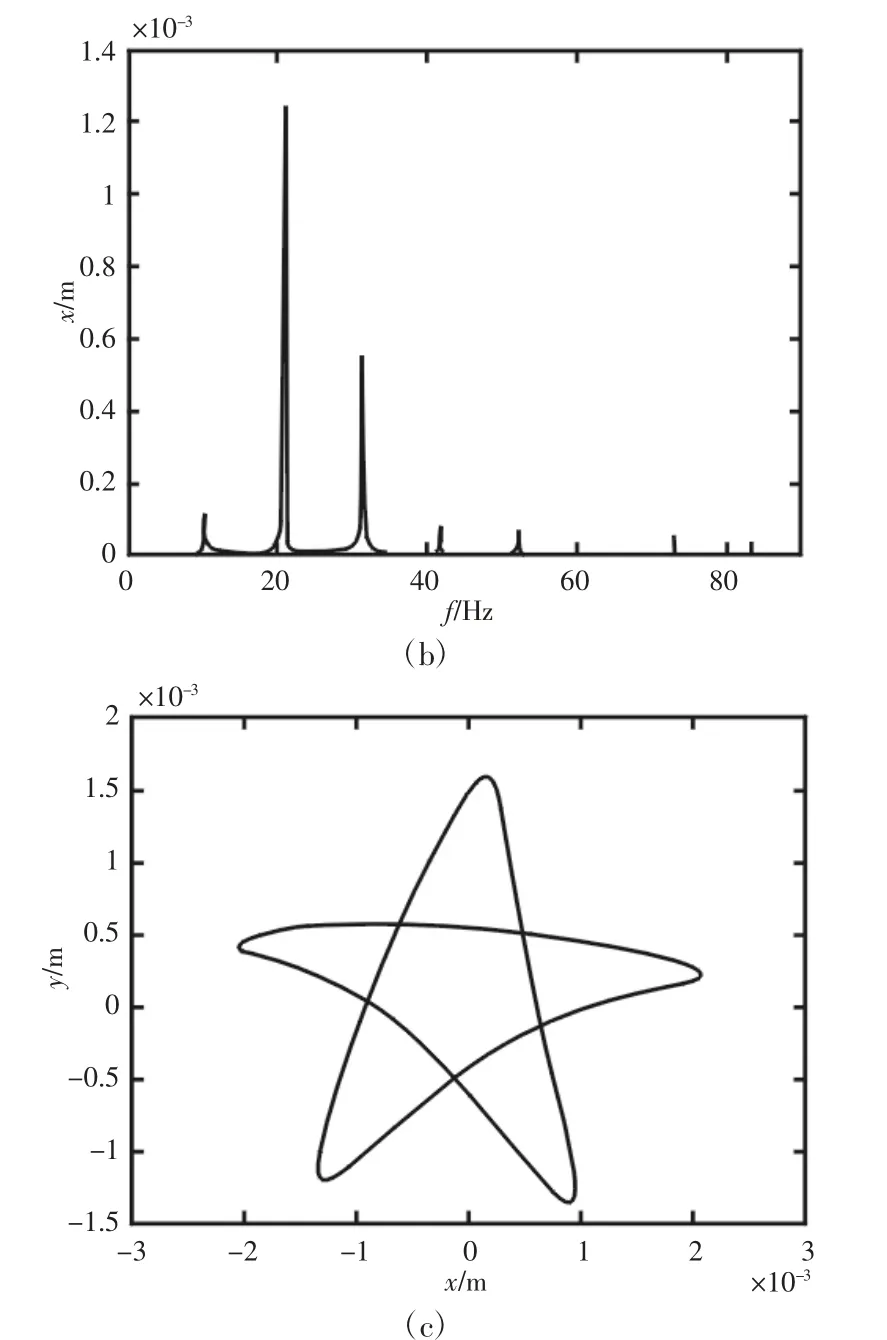
图5 n=1250r/min 时，定子电流频谱、振动位移频谱及转子轴心轨迹Fig.5 Stator Current Spectrum，Vibration Displacement Spectrum and Rotor Axis Trajectory in State of n=1250r/min

4.2 转速一定时，动静碰磨随偏心距大小的变化情况

偏心距作为影响转子不平衡运动的重要因素，其大小的变化势必会对转子系统的动静碰磨情况产生作用。设置转速n=600r/min，取偏心距e 的大小分别为0.0001m，0.0003m，0.0005m和0.0007m 进行仿真得到对应偏心距条件下的定子电流谱，转子振动位移谱与轴心轨迹图，频谱图的纵坐标采用分贝（dB）单位以便于对幅值较小的特征频率分量进行观测。对图6～图9 进行综合观察，随着偏心距加大，电流谱中50Hz 基频两侧的转子倍频成分的调制现象更加显著，再由振动谱可以发现高倍频成分幅值明显加大且逐渐接近工频幅值。轴心轨迹的形状发生从单侧内凹逐渐到双侧内凹的变化，最后当偏心距为0.0007m 时呈内套现象。由上分析得出在固定转速连续加大偏心距也会使转子不平衡运动加剧，运动范围变大造成转子系统的碰磨程度加重，反应到频谱中倍频成分幅值越来越大，如表1 所示。

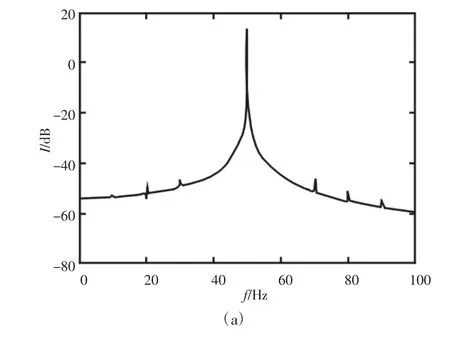
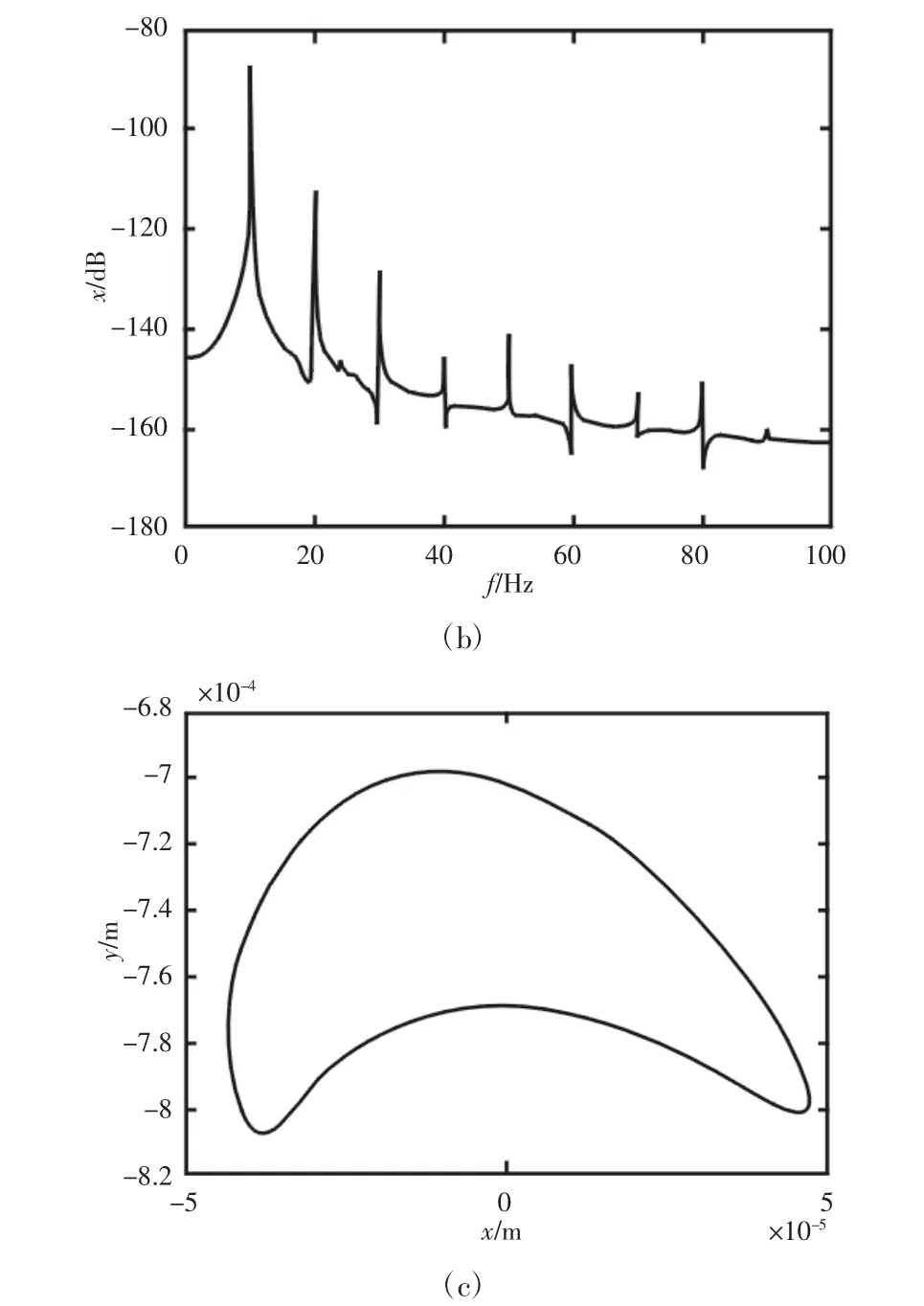
图6 e=0.0001m 时，定子电流频谱、振动位移频谱及转子轴心轨迹Fig.6 Stator Current Spectrum，Vibration Displacement Spectrum and Rotor Axis Trajectory in State of e=0.0001m

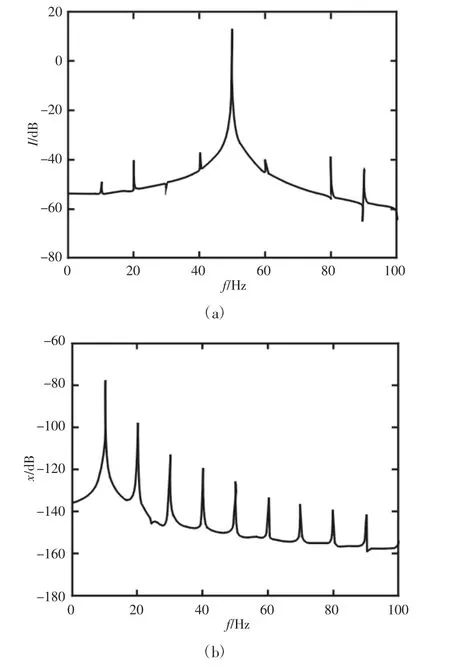
图7 e=0.0003m 时，定子电流频谱、振动位移频谱及转子轴心轨迹Fig.7 Stator Current Spectrum，Vibration Displacement Spectrum and Rotor Axis Trajectory in State of e=0.0003m

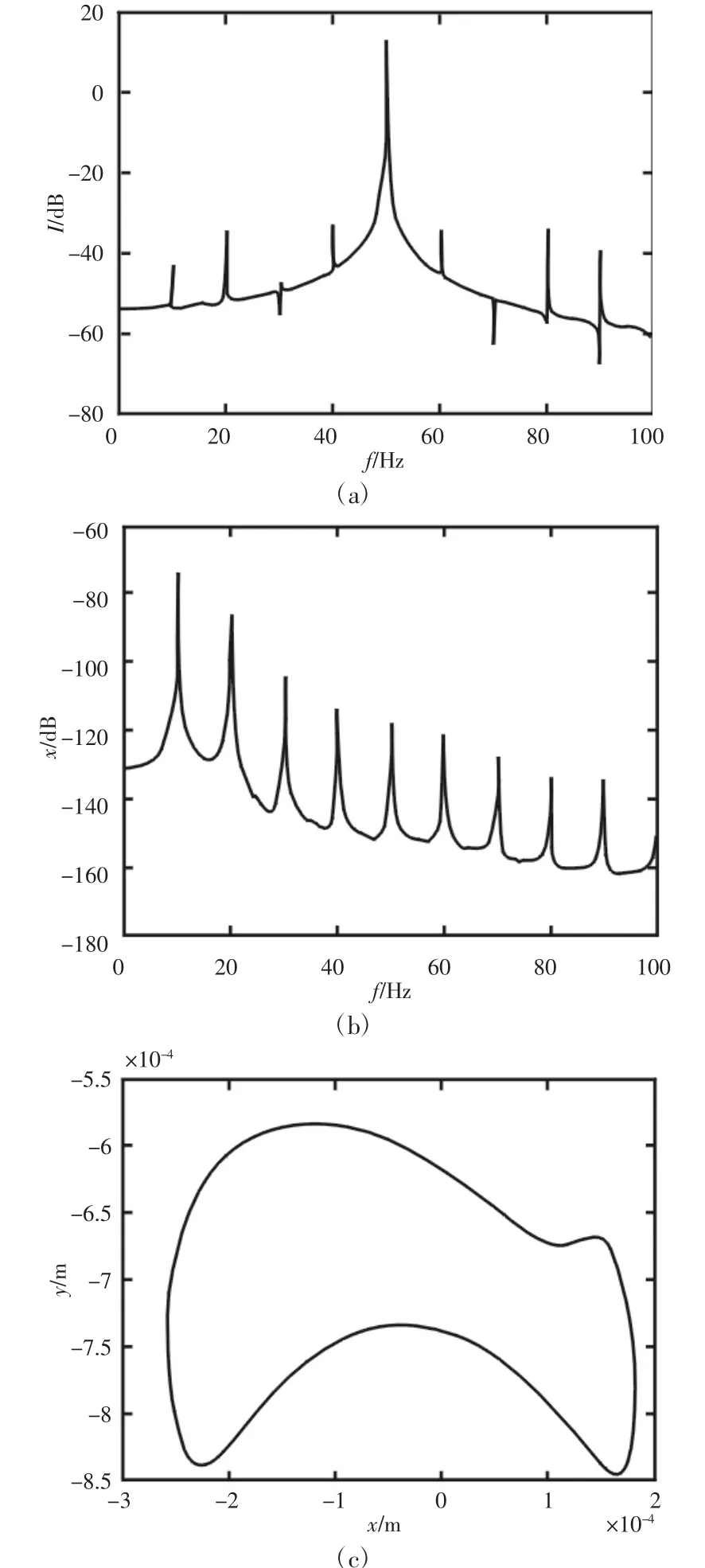
图8 e=0.0005m 时，定子电流频谱、振动位移频谱及转子轴心轨迹Fig.8 Stator Current Spectrum，Vibration Displacement Spectrum and Rotor Axis Trajectory in State of e=0.0005m

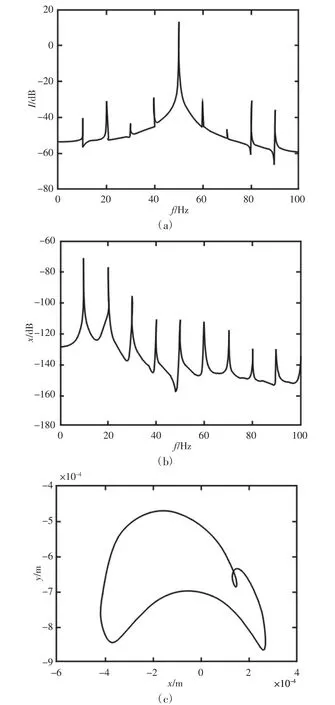
图9 e=0.0007m 时，定子电流频谱、振动位移频谱及转子轴心轨迹Fig.9 Stator Current Spectrum，Vibration Displacement Spectrum and Rotor Axis Trajectory in State of e=0.0007m

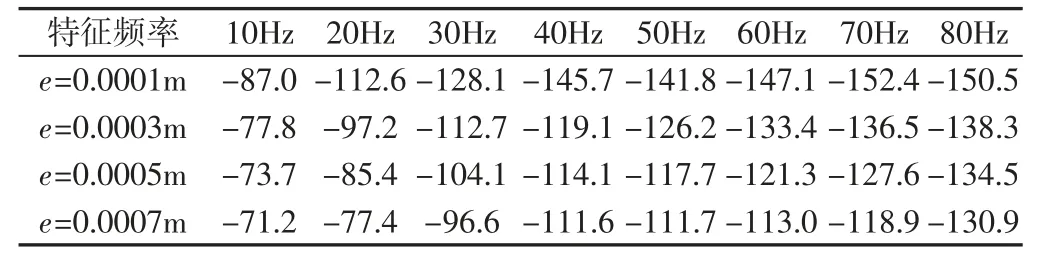
表1 不同偏心距下振动谱的特征频率峰值（dB）Tab.1 The Table of Characteristic Frequency Peak of Vibration Spectrum under Different Eccentricity（dB）

5 结论

在考虑圆盘质量偏心因素的基础上，建立了转子在发生碰磨情形下的弯扭耦合振动数学模型，对转子所受碰磨力进行求解并推导出转子系统碰磨弯扭耦合运动微分方程。结合异步电机模型，以电磁扭矩为纽带建立了转子系统碰磨机电耦合模型，分别控制转轴转速与偏心量来进行仿真实验以研究转子发生碰磨时的电机定子电流特性，同时分析振动信号和绘制轴心轨迹用来作为对比验证，得出结论如下：

（1）当转子系统的转速较小或偏心量很小时，在整个旋转过程中转子的不平衡运动位移都将小于动静间隙，碰磨现象不会发生且电流谱中只有单一工频成分调制。

（2）升高转速或加大偏心距都可以使转子的不平衡运动加剧继而动静件发生接触产生碰磨，此时振动谱有高频分量出现，在对应电流谱的基频两侧都能找到高倍工频谐波分量。当碰磨变得更加严重时，会激励出半倍频成分。

（3）不同碰磨情况下，电流谱中激励出的特征谐波分量呈不同特点，振动谱中的频率成分与轴心轨迹的形状也各有变化，结合频谱分析与轴心轨迹图可以判断碰磨程度的严重与否。

综上所述，可以通过监测电机的定子电流来对转子系统的碰磨故障进行诊断，这为转子系统动力学与故障诊断研究提供了新的理论手段，但要想得到碰磨故障的全面信息，对相关信号进行更细化的处理将是下一步研究的重点内容。