合数模上Hardy和的均值
2020-10-21岳霞霞
岳霞霞
山西工程技术学院基础部,山西 阳泉,045000
其中表示对同时满足pα|q与 pα+1⫮q的所有素数p求积,为任意小的正数.
0 引言
DirichletL-函数[2]与Hardy和是数论研究的核心内容之一.近年来,一些学者对此开展了全方位而多层次的研究,取得了丰硕的理论成果.
徐哲峰与张文鹏[3]研究了当k=p为素数的情形下,短区间上 Hardy和的均值,并得到了命题.
在文献[4]中,Liu W用类似的方法得到下面渐近公式.
命题2 设p≥5为素数,则
Wang X[5]推广了素数模上 Hardy 和的均值性质,得到如下结论.
命题3 设q≥5为奇数,则有
本文利用特征的基本性质,在命题2 和命题3的基础上,将进一步研究合数模上Hardy 和的均值,其主要结果如下.
定理1 设q≥5为奇数且3⫮q,则有
本文的第1节给出了相应的Dirichlet 级数的恒等式,在第2节中将Hardy 和转化为DirichletL-函数,并计算的DirichletL-函数的均值,最后估计Hardy和的均值,给出定理1 的证明.
1 关于Dirichlet 级数的恒等式
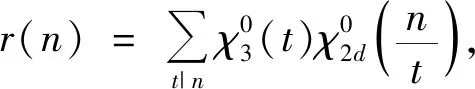
证明 由于r(n)是可乘函数,可得
根据Euler 乘积公式,有
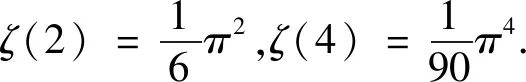
2 Dirichlet-函数的均值
定理3 设d为奇数,且m|d,k为给定的正整数,则

因此有
∶=M1+M2+M3+M4
(1)
由分拆恒等式,可得
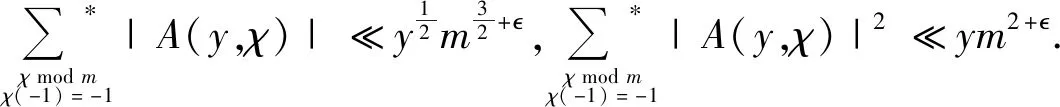
(2)
同理可得
(3)
利用 Cauchy 不等式,有
(4)
结合公式(1)~公式(4) 可得
(5)
设gcd(a,m)=1,根据文献[7]有
从而
∶=M11-M12
(6)
由于r(n)< M12< (7) 现在计算M11.对n1和n2的求和式分成如下四种情况进行讨论: 不难证明 (8) (9) 与 (10) 结合公式 (5)~公式(10) ,取N=m3,可得 利用特征和的 Fourier 展式[8],有 由文献[9,10]及文献[11~13],可得 因而3 Hardy和的均值
