Micromine软件在某金矿床资源储量估算中的应用
2020-10-21车海龙
车海龙
吉林省第四地质调查所,吉林 通化 134001
0 引言
本文主要对该矿床以往形成的地质资料的收集及综合研究,结合已知的成矿地质特征,采用Micromine软件进行数据处理,分析矿体矿床内金矿体的空间分布规律、规模、产状及矿石质量等变化情况,建立数据库、圈定矿体、样品分析、建立矿床三维实体模型、变异函数分析与统计,运用地质统计学中的克里格法进行对金矿体进行资源储量估算[1]。
1 建立地质数据库
数据库是为建立三维实体模型提供数据的基础,为了实现地质资源信息的数字化管理,建立地质资源基础数据库是最基础的内容。地质资源基础数据库通过收集钻孔、测量等数据信息,建立、存储地质资源信息数据表。数据库是以一定的组织方式存储在一起的相关数据的集合,它能以最佳的方式、最少的数据冗余为多种应用服务,地质数据库是数据库技术在地质勘探和矿山工作中的实际应用,是矿山资源储量估算和采矿设计的基础[2]。
本次工作利用41个钻孔数据,形成井口坐标表、钻孔弯曲度测量表、样品分析表和岩性表(见表1至表4)。将原始数据输入Micromine软件,经过钻孔数据效验,确保数据在转抄、转换和导入过程中无错误发生。最后形成Micromine地质数据库。
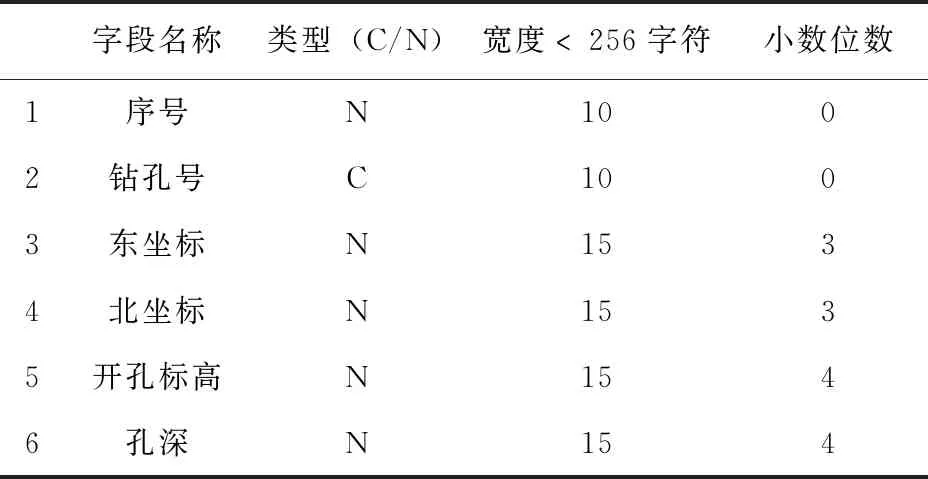
表1 钻孔孔口文件数据结构
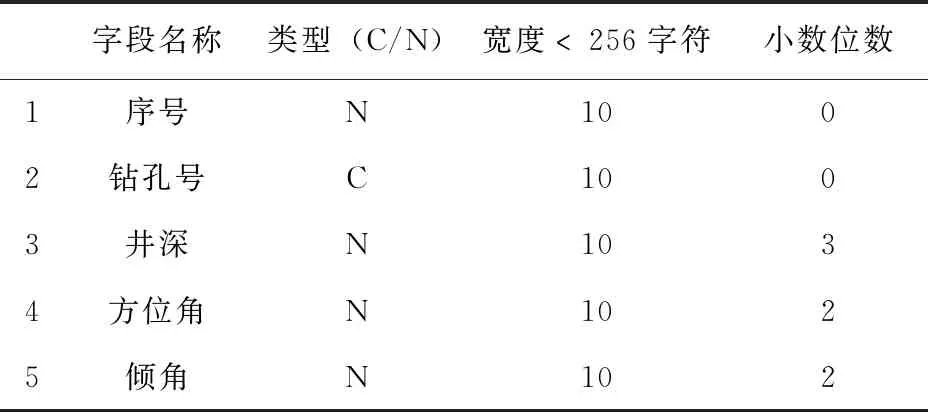
表2 钻孔测斜文件数据结构
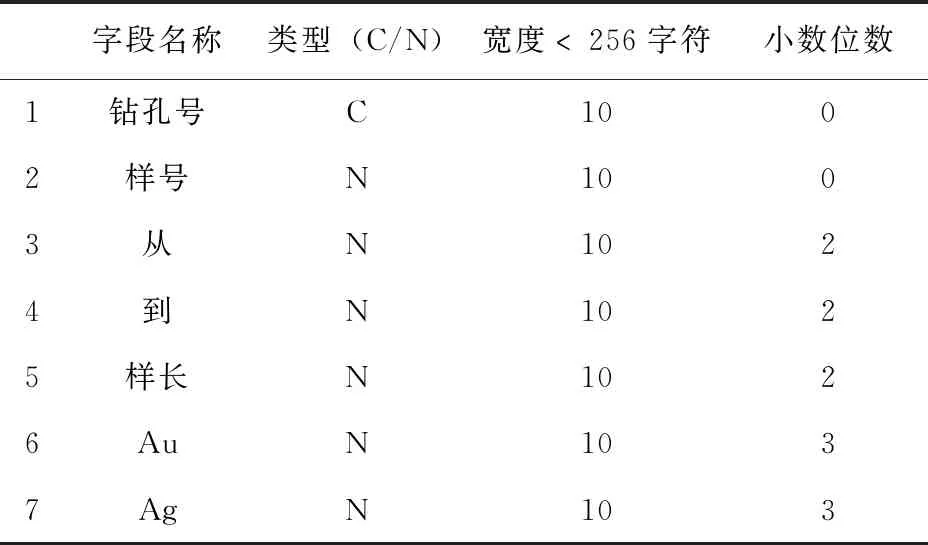
表3 样品化验文件数据结构
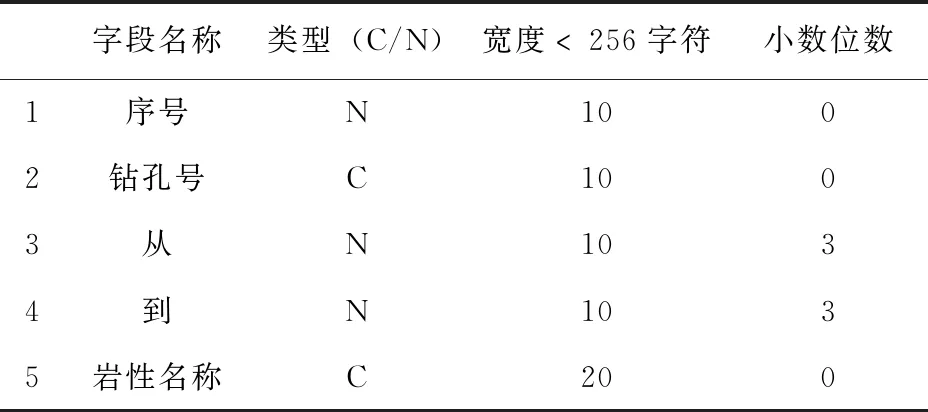
表4 岩性文件数据结构
2 建立实体模型
本次参加资源储量估算的工程所在勘查线从南西至北东共12条,按照工业指标和矿石类型分别在各勘查线剖面上进行矿体的圈连,并对其剖面地质信息进行了解译,生成地质勘查线剖面图。
在生成地质勘查线剖面图后,将相邻勘查线剖面上的矿体轮廓线依次用三角面进行连接,形成一系列三角面围成的复杂曲面,形成矿体三维实体模型(见图1)。

图1 矿体三维实体模型Fig.1 Three dimensional solid model of ore body
3 样品数据分析及特高品位处理
对样品统计分析及特异值处理时,应以矿体为单位进行。对区域化变量进行估值前,分别绘制区域化变量的分布直方图、累计频率分布曲线或概率图等,判断其分布特征,并计算区域化变量的统计特征,如最小和最大值、样品数、平均值、中值、方差、标准差、偏度、峰度和变化系数等。
3.1 样品数据分析
区内最大矿体内样品数量=154个,最小值=0.37×10-6,最大值=58×10-6,均值=6.54×10-6,标准差=8.38,变异系数=1.28。西舍尔估值=6.46[3],具体数据见图2。经过对样品数据的分析,发现该矿体存在特高品位,需要进行特高品位处理,利用Micromine软件计算储量特高品位的剔除,选取分位数97.7%所对应的金品位值30.20×10-6为截止值,将样品中所有>30.20×10-6值替换成30.20×10-6。

图2 矿体样品统计分析图Fig.2 Statistical analysis of ore body samples
3.2 样品等长组合
地质统计学要求参与估值计算的数据的支撑(指样品的长度或体积)应该一致,组合样的目的就是将空间不等长的样长和品位量化到一些离散点上,即每段样长的中点,只有在工程方向上产生均匀(即等距离)的离散点,才可用于资源储量估算。因此,组合样产生的离散点,将用在矿体的块模型中,以便进行估值等后续操作。进行样品组合时,组合长度由统计学的方法确定,根据组合长度组合品位采用样长加权平均法。
本次样品组合长度等于平均样品区间长度,采用样长加权平均法进行。通过对研究区内矿体样品组合直方图分析,一般样长为0.6~2.1 m,样长1 m的基本分析样品数量较多,占样品总数50%以上,如以1 m样长为组合长度,大部分分析数据在组合后将不会改变,将保持大部分样品的原貌,最终确定1 m样长为组合样长。
4 变异函数及结构分析
4.1 变异函数
为表征一个矿床金属品位等特征量的变化,经典统计学通常采用均值、方差等一类参数,这些统计量只能概括该矿床中金属品位等特征量的全貌,却无法反映局部范围和特定方向上地质特征的变化。地质统计学引入变异函数这一工具,它能够反映区域化变量的空间变化特征——相关性和随机性,特别是透过随机性反映区域化变量的结构性,故变异函数又称结构函数。
我们可以把一个矿床看成是空间中的一个域V(见图3),V内的许多值则可以看成是V内一个点至另一个点的变量值,如图中x,x+h为沿x方向被矢量h分割的两个点,其观测值分别为Z(x)及Z(x+h)[4],该两者的差值[Z(x)-Z(x+h)]就是一个有明确物理意义的结构信息,因而可以看成是一个变量。
在主震之后的地震活跃期间,可在不同的位置几乎同时发生多个地震。在这种情况下,由地面传感器测到的地震波包含不止一个震源的混合信号。如果探测算法假设仅为一个地震,那么估计出的地震参数(比如位置和震级)就不会精确。而这些不精确的估计也会导致虚报,这种情况在大地震后经常出现。
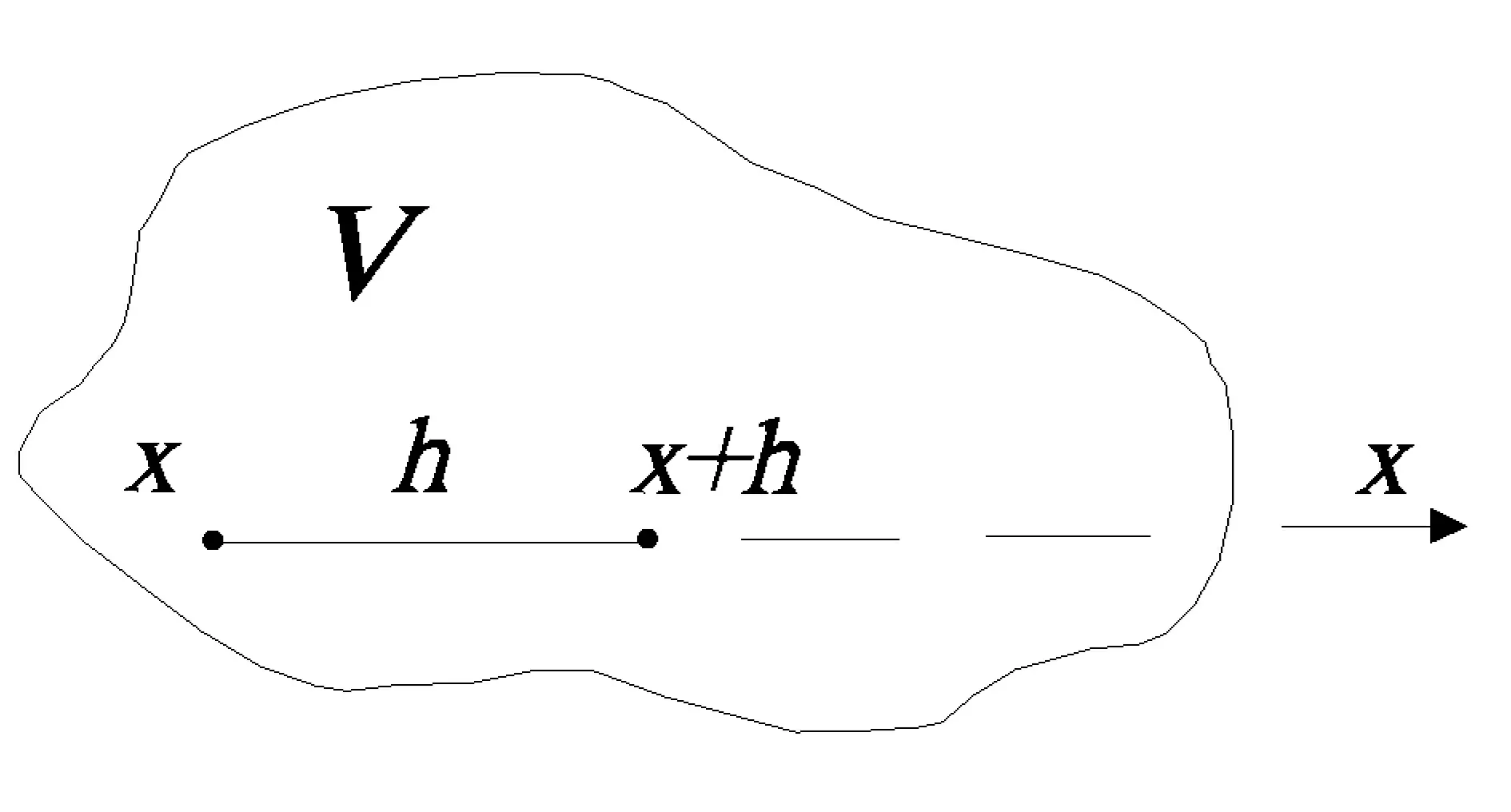
图3 域V内的变量值Fig.3 Variable values in Domain V
区域化变量Z(x)在空间相距h的任意两点x和x+h处的值Z(x)与Z(x+h)差的方差之半定义为区域化变量Z(x)的变异函数,记为γ(x,h):
由上式可以看出,γ(x,h)是依赖于x和h两个自变量的,γ(x,h)与位置x无关,而只依赖于分隔两个样品点之间的距离h时,则可把变异函数γ(x,h)写为:γ(h):
在实践中,样品的数目总是有限的,把有限实测样品值构制的变异函数称为实验变异函数(experimental variogram),记为γ*(h):
γ*(h)是理论变异函数值γ(h)的估计值。
变异函数一般用变异曲线来表示。其常用的模型有:球状模型、高斯模型及指数模型。
4.2 变异函数计算及拟合
利用样品等长组合数据,分别计算矿体的试验变异函数,并用球状模型的理论曲线进行拟合[5]。按照估值搜索椭球体的概念给出矿体的主方向、次方向和第三方向的变异函数,拟合结果如图4至图6。
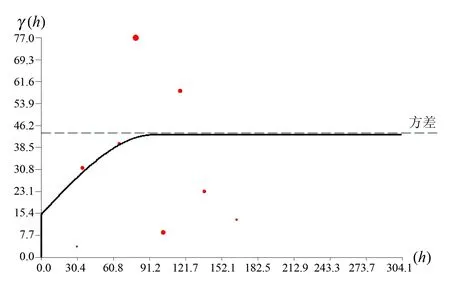
图4 矿体主轴变异函数Fig.4 Variation function of ore body principal axis
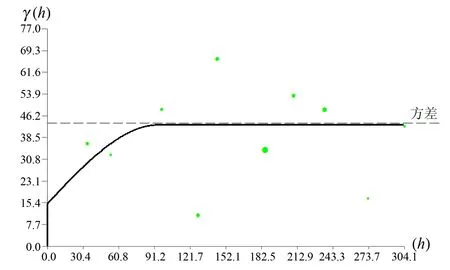
图5 矿体次轴变异函数Fig.5 Variation function of secondary axis of ore body
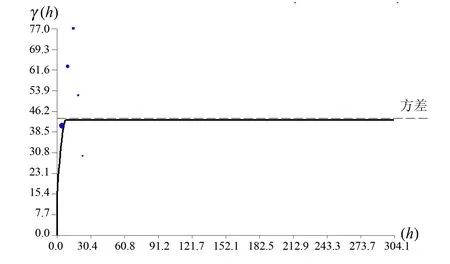
图6 矿体第三轴变异函数Fig.6 Variation function of the third axis of ore body
4.3 结构分析
结构分析的主要方法是套合结构,就是把分别出现在不同距离上和不同方向上同时起作用的变异性组合起来代表整个矿体的变异结构。具有几何异向性变异函数的套合方法是用一个球状模型来表征各个方向的变异性,具有相同的C0值和基台值C而具有不同的变程值a。目前国外软件只支持几何异向性,在矿业软件中要求三个方向的模型类型和数目、块金值和基台值一致,因此只给出变程最大、连续性最好的主轴的变异函数参数,用球状模型拟合了主轴方向的变异函数。品位估值时要求给出:块金常数C0、主轴方向的变程a, 主轴方向的基台值C。再给出次轴/主轴和最小轴/主轴的比值。在Micromine软件中要求只给出主轴的变程a,再给出次轴/主轴和最小轴/主轴的比值[3]。矿体金品位变异函数结构分析结果如表5所示。

表5 矿体金品位变异函数结构分析结果
4.4 交叉验证
为了验证搜索椭球体方位和变异函数结构模型是否正确,是否符合实际。通过不断地调整搜索椭球体方位和变异函数参数,重新计算误差的均值和方差及克立格估计方差。直到误差的均值趋近于“0”,以及误差方差/克立格估计方差趋近于“1”时,变质函数的结构参数才是最优的[4]。
本次估算中主矿体在中部位置产状上发生变化,故将其分割成东西两部分(具体参数见表6),最终矿体球状模型参数(见表6):矿体东部球状模型的参数:C0=15、C=29、主轴的变程a=95 m、次轴变程/主轴变程=0.95、第三轴变程/主轴变程=0.06。交叉验证判别指标:估计误差均值=0.034 659、估计误差方差和克里格估计方差比=0.998 80;矿体西部球状模型的参数:C0=15、C=29、主轴的变程a=95 m、次轴变程/主轴变程=0.95、第三轴变程/主轴变程=0.06。交叉验证判别指标:估计误差均值=0.071 904、估计误差方差和克里格估计方差比=1.059 3。
验证结果表明所确定的理论变异函数各参数合理,认为满足普通克里格估值精度的要求。

表6 矿体交叉验证后金品位变异函数结构分析参数表
5 普通克里格估值及储量估算
普通克里格法是地质统计学中资源量估算应用最广的方法,是以区域化变量理论为基础,以变异函数为主要工具,对既有随机性又有相关性的空间变量(通常为矿石品位等矿体的属性)实现最优线性无偏估计的方法。主要在变异函数结构分析的基础上,求插值过程中的最优线性无偏估计量。根据研究目的和条件不同,选取不同的克里格法进行估值计算。对本研究区进行区域化变量分析发现,研究区区域化变量服从正态分布时,故采用普通克里法进行估值。
5.1 建立矿床矿块模型
块体模型是矿床品位及资源储量估算的基础。建立块体模型的基本思想是将矿床在三维空间内按照一定的尺寸划分为一定的单元块,然后对整个矿床范围内的单元块的品位根据已知的样品进行估计,并在此基础上进行资源储量估算。
该矿床基本工程间距为40 m,矿体品位变化系数为127.30%。综合考虑,最终将资源储量估算所使用的块模型尺寸定义为:东10 m×北5 m×垂向5 m,次分块的尺寸为:东5 m×北2.5 m×垂向2.5 m。通过矿体实体模型与矿块模型(图7)对比,发现二者形态吻合较好,矿块尺寸选择合理[1]。
5.2 普通克里格估值
采用普通克里格法估算矿块品位,除了需要输入搜索椭球体参数外,还要输入变异函数结构参数:块金常数C0、基台值C、变程a。注意如果有2个变异函数套合结构则:块金常数C0只有一个、基台值C有两个、变程a有两个。注意目前国外的矿业软件只支持几何异向性,变异函数参数只输入主轴(长轴)方向的参数代表其他两个方向。次轴和第三轴只输入轴比,其变程相应缩短。

图7 矿体块模型Fig.7 Ore block model
本次在Micromine软件中,根据所确定的理论变异函数各结构参数,同时结合对矿床地质特征的认识,搜索半径按照40 m的基本工程间距做为起始值,按8个扇区,每个扇面最多8个点,最小1个点,每搜索一次半径都增加1倍,分别为40,80,160 m进行搜索,直至所有块的品位值都被估算,完成矿块估值,建立带有品位数据的矿床矿块模型[1]。在估值时可对每一个块都记录估值次数、参与估值的工程数、样品数和样品品位的标准离差。搜索椭球体空间分布形态如图8至图10所示,搜索椭球体设置参数如表7所示。

表7 搜索椭球体参数表
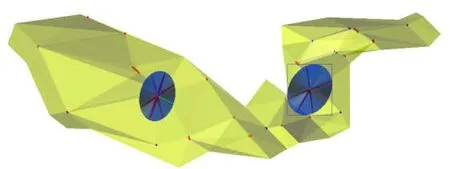
图8 搜索椭球体平面位置图Fig.8 Plan position of ellipsoid searching

图9 椭球体(向东)倾向位置Fig.9 Inclined position of ellipsoid (eastward)
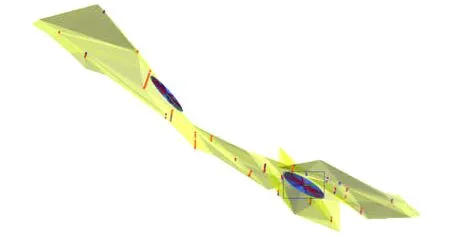
图10 椭球体(向北)倾伏位置图Fig.10 Tilting location of ellipsoid (northward)
5.3 储量估算
对于带有品位数据的矿块模型,可以按照不同标高、不同边际品位、不同矿石类型及不同储量基本等标准进行全面的统计分析。本次为了更好的确定克里格法估值的可靠性,采用距离幂次反比对进行验算,与地质统计学估值结果进行对比分析,详见表8。
从表8可以看出两者估算结果比较接近,相对误差矿石量为2.72%、金属量为3.36%,平均品位为0.007%。表明本次资源储量估算采用的方法是合理的,结果是可靠的[3]。

表8 资源量验证结果对照表
6 结论
(1)通过建立矿床三维实体模型,对矿床的数据进行了数据化,提高数据的利用率和分析能力,为地质工作人员和矿产生产单位在三维空间中观察、分析矿床的成因、矿体空间展布特征、产状等信息提供了全新的分析研究方法[2]。
(2)通过本次采用地质统计学进行资源储量估算,发现运用三维软件计算储量避免了人工的大量计算和人为因素导致的错误发生,大大的提高了工作效率,并且能够运用多种发放进行资源储量对比,提高了计算结果的准确性和可靠性。为矿山下一步工作和开发利用提供详实、可靠的地质依据。
