惯性权重矩阵下的自适应粒子群算法分析

杨宝军

(太原学院 应用数学系，山西 太原 030012)

PSO是以群集智能为基础的一种随机搜索算法，由Kenedy与Eberhart在1995年首次推出。PSO具有方便易用、可调节参数不多等特征，广泛应用在神经网络权值的训练、函数优化、控制系统参数优化等[1]。然而，在实践过程中，PSO存在出现局部极数、收敛效率低下等缺陷[2]。可以从下面几个方面进行改进：1)利用粒子速度参数、CBPE、多元性等来进行设置[3]；2)把GA算法和蚂蚁算法与PSO进行融合[4]；3)优化粒子位置变化规律或者使用变异策略[5]。因此，寻找1种以惯性权重矩阵为基础的自适应粒子群算法极为重要。基于此，本文从离散状态空间表达式入手，得出算法稳定使用时参数约束条件与粒子的运作规律，引进使算法每个步骤以较大概率收敛、较小概率发散的参数组合选取策略、惯性权重矩阵策略，以及按照粒子活跃度速度重置与历史最优值扰动策略，以期获得改进后的RDR-PSO，初步解决当前PSO存在的缺陷。

1 粒子群算法分析

1.1 基本粒子群算法

在PSO稳定使用时，对于第i个粒子来说，其后的位置序列xi(k+1)会被速度vi(k)、位置xi(k)、个体最优位置pi(k)、群体最优位置gi(k)这些特殊的信息序列和某些不稳定原因的影响。其变化步骤如下：

关于速度信息更新的相关模型

vi(k+1)=ωvi(k)+c1r1(pi(k)-xi(k))+

c2r2(gi(k)-xi(k)).

(1)

关于位置信息更新的数学模型

xi(k+1)=xi(k)+vi(k+1).

(2)

式中：ω为惯性权重；k为目前迭代频次；c1，c2为学习因素；r1，r2为0到1之间均衡分布的随机值，表示粒子所处环境的随机影响要素。

从PSO的运动情况进行分析，大量学者对于这种算法的收敛性做出讨论，为后续的改进方式打下基础，因此，从离散状态表达式入手，明确这种算法的稳定性，提出这种稳定性条件下算法使用时的数值要求十分重要。

假设群体粒子数量是n个，寻找最优解搜索空间是m维，φ1(k)=c1r1(k)，φ2(k)=c2r2(k)，则为了确保普适性，把式(1)、式(2)表示成

V(k+1)=ωV(k)+φ1(k)(P(k)-X(k))+

φ2(k)(G(k)-X(k))，

(3)

X(k+1)=X(k)+V(k+1).

(4)

式中：ω，φ1(k)，φ2(k)都是n×m维对角矩阵；X(k)，P(k)，G(k)，V(k)都是n×m维矩阵。

因此，有着下面的定义：

定义1：e1，e2属于数值不变的常量，若∃k≤Kmax，这时就有Vij(k)=e1∪Xij(k)=e2，说明这个方法能够在长时间内被较好地使用。

定理1： PSO算法可以长期运行的要求是

(5)

定理2：在标准PSO算法稳定运行的情况下，假设K→Kmax，全部粒子速度是0，并且位置收敛于一点。

1.2 惯性权重ω和中间量φ的影响

据前文，在定理2中，算法如果要长期运行，就需要任意k的ω(k)，φ(k)，也就是式(5)中曲面相交的地方，因为表达式较为庞杂，变化成式(6)，通过图形的方式给出各种参数组合下算法的稳定运行状况。

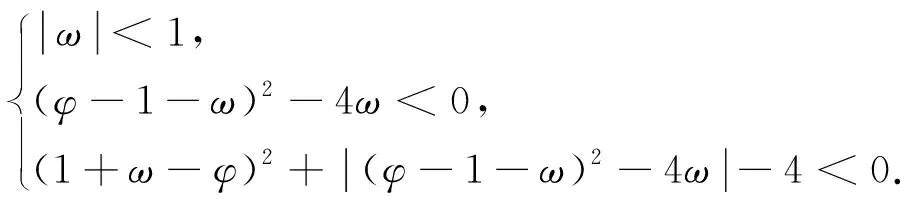
(6)

以x轴作为ω，y轴作为φ，图中黑色的部分是z≡0的部分，当区间位于-1.5<ω<1.5，-1.5<φ<1.5的时候，如果进行投影，就可以得到图1。

图1 算法的稳定性关系

从图1可以看出，在任一时刻k惯性权重ω，φ在黑色空间内时该离散时间系统可以长期使用。假设长期运作时要求-0.5<ω<1，ω为式(3)的相关矩阵，在不考量干扰的条件下，速度的运行轨迹为

V(k)=ωkV(0).

(7)

式中：V(0)为速度的初始情况。

从上述分析能够发现，确保系统稳定使用时，即ω，φ在所有的时间范围之内，他们的k的取值都是在黑色的位置，式(3)的所有粒子速度的值都会变得比较小。如果基于理论角度出发来看，这其中的差异就在于0<ω<1时，速度V的响应为单调衰减，符号不变；如果有-0.5<ω<1，那么V的响应则会变成正负交替，在震荡中呈现出衰减的趋势。这么来看，基于某种角度进行分析，当ω在寻找最优解环节中可正可负时拓展粒子的搜索空间与速度V状态轨线的庞杂性，使得这种方式能够更好地在迭代环节中发现最优解。

2 标准粒子群算法的改进

为了进一步提升PSO算法的性能，主要从ω，v与历史最优值入手，阐述改进方式及其因素，逐步使用本文指出的以惯性权重矩阵作为基础的RDR-PSO算法。

2.1 随机惯性权重矩阵的引入

本文提出使得粒子在所有步骤都有较强的概率收敛、较小的概率发散的参数组合选择方式，此类形式不仅能够确保所有粒子的广泛分布，还能够保证算法有较强的稳定性。不过所有粒子的搜索路线还是有盲目性的特征，所以文中为所有粒子所有维速度在每一步骤独立设计1个随机性的ω，并且其权重能够是正值或者负值。利用这种方式能够为粒子的速度与位置变化带来随机性，造成运动状况更为庞杂，这是为了尽量减少扩大搜索范围而产生的盲目性。

这时式(3)表达为

V(k+1)=(ωmin+(ωmax-ωmin)rand(n,d))V(k)+

c1r1(P(k)X(k))-c2r2(G(k)X(k)).

(8)

式中：d为待改进函数自变量的数量;n为原始粒子数量;ωmin，ωmax为速度所有维允许的惯性权重的极值;X(k)，V(k)，P(k)，G(k)各自是n×d维位置、搜索速度、个体历史最优点、全局最优位置矩阵，其中，G(k)中数值都相同，(ωmin+(ωmax-ωmin)rand(n,d))就是为了提升其性能，继而运用n×d的矩阵。

基于上文分析，具体数值为

(9)

式中：ω(k)为n×d维矩阵，此时各个环节k达到1个条件：P发散>P收敛，意味着该方式有着良好的收敛性。

为了更好地阐述对于各个步骤来说，每个步骤都是其中各个维度的定义惯性权重参数，且是具有优势的，然后对其设定变量c1=c2=0.5∪ω递减、c1=c2=2∪ω递减以及c1=c2=2∪ω矩阵，然后对3种情况进行分析，在这些状态下，粒子的原始状态为：X(0)=[5-5]，V(0)=[-32]。

2.2 定义粒子活跃度

速度在0的均衡点得到稳定收敛，所以可以将全部的粒子在k时间里的活跃情况认为是每个维度上的绝对速度的极值，也就是

Di(k)=max(|Vi(k)|).

(10)

式中：Di(k)代表在第k步时第i个粒子的活跃情况。

从式(10)可知，Di(k)数值越小，速度越慢，其搜索最优解的性能越不好，越接近于局部最优解。假设Di(k)较小时，其搜索范围将会不断缩小，这时有助于找到局部最优解，不过无法提升全局搜索速度，就是均衡算法的全局寻优性能与局部寻优性能，为Di(k)设定一个极值Dmin，而且设置1个常数klimit，假设Di(k)在连续的相应的次数比Dmin要低的时候，就说明这个例子具有比较低下的活跃度。

3 基于惯性权重矩阵的自适应粒子群算法

在上述的讨论中，当某一粒子的活跃程度不高时，说明速度越低，这时粒子位置信息与速度信息不会变化，呈现早期收敛情况，算法无法使用。本次通过速度与位置更新，使得这种粒子再次进到搜索环节，能够确保在这种算法使用中全部粒子长期处于寻优状态，从而提升粒子使用率。这时所有粒子的pi(k)≈G(k)，为了确保重置的粒子可以受到全局最优位置与个体历史最优位置的共同作用，使用个体历史最优位置干扰方式，使其位置参数发生变化，进而拓展寻找范围。

从上述分析能够发现，这种改进的算法保留了原有算法方便易用的特征，其存在的差别如下：

1)速度更新公式由(1)变成(8)，其中的不同就是以惯性权重矩阵作为基础。

2)在速度更新公式里面，上面一个步骤的速度v(k)和历史当中最优序列p(k)在当前的叠代过程中出现变化。推断其有无出现变化的基础是：第i个粒子的活跃程度Di(k)有无持续klimit次低于临界值Dmin，“是”则代表v(k)中第i行参数更新，同样地对于p(k)中第i行参数给出1个干扰作用。

3)本次使用的历史最优值干扰方式就是(β1+β2-β1)×rand)+1)×pi(k)，其中，β1，β2为扰动数值，而非(β1+β2-β1)×rand)×pi(k)，由于这时所有粒子历史最优位置会迅速减退至0 ，对于最优解在0时的能力评估的函数还是比较有用的，但是这会让算法的使用缺乏相应的价值。

4)对于参数组合策略来说，按照式(9)来进行选择。其中，具体步骤与上文提出的一样，在这里不一一说明。

4 算法测试

在对本次指出的RDR-PSO算法展开仿真比较验证过程中，了解Dmin参数选择的差异，将直接关系到算法性能，同样地为了掌握本次算法的优点，先是简要说明6种基本测试函数，之后对RDR-PSO算法性能展开仿真试验，具体如下。

4.1 基本测试函数及介绍

本文基于6个种类的函数来对文章提出的算法进行测试，测试算法查询最优解的能力，这些函数有着不一样的极数，其名称、公式和最优值具体见表1，其中，Sphere表示单峰函数，只有1个极数，寻找最优解没有太大难度。Rosenbrack函数是病态函数，其极数存在于1条缝隙中，而其它函数都是多峰函数，在搜索范围内有着若干极数，寻找最优解比较困难。本文基于表1中的6种函数，对本文算法的能力进行测试。

表1 6种测试函数及极值

4.2 不同Dmin参数对算法性能的影响

在本次仿真验证过程中，将初始粒子数量设定成80，klimit数值是2，惯性权重矩阵按照[-0.5，0.8]进行取值，参数设置是10-1，10-2，10-3，10-4，10-5。最大叠代设定成2 000。所有测试函数搜索区间是[-10，10]，对于所有函数10维、20维、30维时RDR-PSO算法单独运作20次，其结果可见各种Dmin数值对于不同测试函数在同样的其他情况下其结果准确度存在差别，从总体结果能够发现，在Dmin参数选取10-3或者10-4时算法对于各种测试函数都能实现良好的搜索效果，因此，在之后的比较研究中并未特别说明，都将Dmin参数设置成10-4。

5 结束语

PSO随机搜索算法因为具有易出现局部极数、收敛效率低的缺陷，本文从离散状态空间表达式入手，探讨粒子群算法的稳定性，获得改进后的自适应粒子群算法(RDR-PSO)，并对RDR-PSO进行仿真验证。结果表明，改进后的PSO算法与标准PSO算法性能进行比较分析，得到RDR-PSO算法有着可以提升收敛准确度与跳出局部极数的特征，说明RDR-PSO有着收敛准确性高、全局寻优速度快、方便易用，发展前景广阔。然而本文仅从离散状态空间表达式入手来探讨粒子群算法的稳定性，结论并不全面，以后还需深入研究。