不同浮力下水下悬浮丛式管汇水动力分析*
2020-10-21赵宏林周学军王莹莹
徐 宁 赵宏林 周学军 王莹莹 郭 鑫 李 楠
(1.中国石油大学(北京)机械与储运工程学院 北京 102249;2.中海油研究总院有限责任公司 北京 100028;3.中国石油大学(北京)安全与海洋工程研究院 北京 102249)
水下生产系统能够避免海上波浪和恶劣天气等极端海况影响,因而在深水油气尤其是超深水领域中得到了广泛应用[1]。水下生产系统的主要设备包括采油树、管汇、采油泵、压缩机等,这些设备通过不同类型的管线相互连接,从而将油气集输并最终输送到生产终端,如浮式生产储油装置(floating production storage and offloading,FPSO)[2]。
深水海底中地形复杂多变,因此很多学者研究了考虑地形及障碍物条件下的水下管线系统布局方案设计[3-7]。由于地形不平整的约束条件较多,这些研究方案的确定通常需要前期大量的地质勘探工作,布局设计也非常复杂。水下悬浮或漂浮结构一般先通过悬链线或张紧绳进行系泊定位,再由管线输送油气流体。这些悬浮或漂浮设施通常采用系输分离的方式应对风浪较大和海底地形平缓的情况[8-13]。但在流速较低的海底,以系输分离的方式实现系泊通常存在成本高、设计复杂等问题。针对以上问题,本文提出了柔性立管系输两用的新概念方案及以悬浮式水下丛式管汇为中心的全空间布局方案,降低管线使用的复杂性,避免了海床对固定底部基础结构的影响,节省了管汇基础安装时间,缩短了油田建设工期。
如何保持管汇的稳定性是新型水下悬浮丛式管汇正常工作的关键。油气密度、海流作用和浮筒质量是影响管汇稳定性的主要因素[14]。在下放安装、正常工作、水压试验和停产等情况下,油气密度的差异会使管汇与管线的平衡位置发生改变,海流的作用会使管汇产生偏移,浮筒质量的改变同样会使管汇平衡位置发生改变。为此,本文分析油气密度、海流作用和浮筒质量对管汇和管线稳定性主要参数的静态响应特性,并优选出外输管线悬跨长度及浮筒质量参数,使管汇满足稳定系泊的要求。
1 Morison公式及凝集质量法
管线和浮体的水动力载荷采用Morison公式的扩展形式进行计算,即
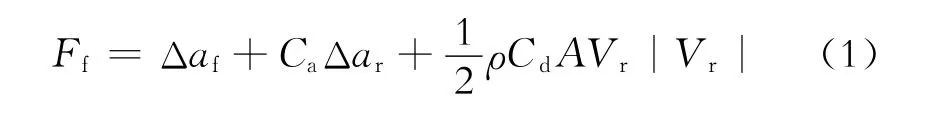
式(1)中:Ff为波浪载荷;Δ为排水量;af为水质点的绝对加速度;Ca为附加质量系数;ar为水质点的相对加速度;ρ为海水密度;Vr为水质点的相对速度;Cd为拖曳力系数;A为拖曳投影面积。
柔性立管在性能上相当于一个非线性弹簧,离散为凝集质量模型,由若干个连续、无质量的分段和处于各分段中点处的节点组成。将其模拟为轴向、旋转弹簧和阻尼器的组合体,节点集中了2个相邻分段的各1/2质量,力和力矩都作用在节点上,这是OracleFlex软件对管道张力建立模型的数学基础。
管线有效张力的计算为
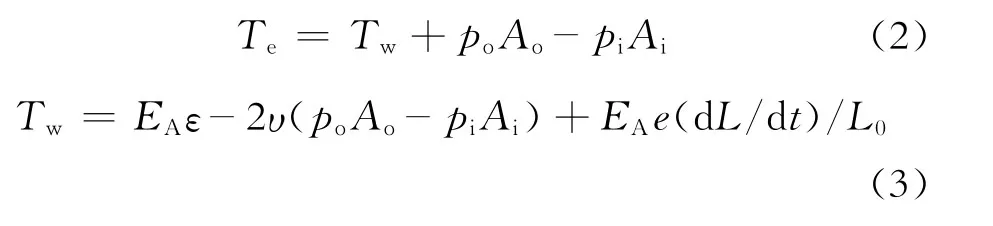
式(2)~(3)中:Te为有效张力;Tw为壁面张力;EA为管道轴向刚度;ε为总平均轴向应变,ε=(LλL0)/(λL0);L为管段瞬时长度;λ为分段伸长系数;L0为管段初始长度;υ为泊松比;pi、po分别为内压力和外压力;Ai、Ao分别为内截面积和外截面积;e为阻尼系数,一般忽略不计;dL/dt为长度变化率。
2 水下悬浮丛式管汇整体模型的建立
2.1 坐标系和风、浪、流方向的确定
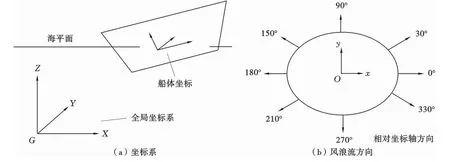
图1 全局坐标系和风浪流方向示意图Fig.1 Schematic diagram of coordinate systems and wind wave flow direction
如图1所示,采用全局坐标系G-XYZ确定坐标轴,其中G代表全局坐标系的起点,不同的物块模型对应各自的局部坐标系。风、浪、流的方向是相对全局坐标系中的GX轴和GY轴而言的。
2.2 管汇与管线模型的建立
水下悬浮丛式管汇模型主要由管汇系统和管线系统两部分组成,其简化结构如图2所示。
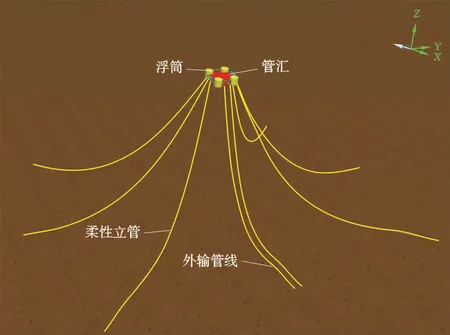
图2 水下悬浮丛式管汇与管线模型Fig.2 Underwater suspended cluster manifold and pipline model
管汇系统包括管汇、鹅颈管和浮筒。管汇和鹅颈管以六自由度(6 D)浮块建模,连接方式为刚性连接。当改变输送流体密度时,与管汇管道内体积相乘,可等效为改变管汇质量。浮筒建模为有直径和高度的六自由度圆柱浮体,通过改变质量来改变浮力。在管汇系泊过程中,预先调节浮筒质量大小,使管汇悬浮在预定高度。在未调节浮筒质量差时,4个浮筒质量均相同。管汇在工作状态时,浮筒质量是一个确定值,无法调节。
管线系统包括柔性立管和外输管线。管汇与管线连接点为8个,左右侧6个接口通过鹅颈管分别与6根内径为φ152.4 mm的柔性立管相连接,管线另一端采用锚固方式。管道单元采用line单元构建,为了使计算结果精确,管汇连接段的节点划分较为密集,设置节点间距为0.25 m,密集段总长度为10 m,其余段的节点划分较为稀疏,节点间距为1 m。另外2根内径为φ304.8 mm的外输管线分别连接在侧面,方向为X轴方向。设置另一端分别通过汇管接头对应连接一清管回路的两端,用以完成汇管清管任务。管线系统的各柔性立管应在各个方向呈均匀辐射布置,便于均布受力。
2.3 参数设置
实际工程的水下情况非常复杂。在计算生产系统的系泊情况时,设定系泊水深1 000 m,设定管汇系统的主要尺寸(图3)并对其主要参数进行简化(表1),其中输送油气体积为管汇管道内部的体积量。柔性立管、外输管线和百年一遇水下流速参数见表2、3。
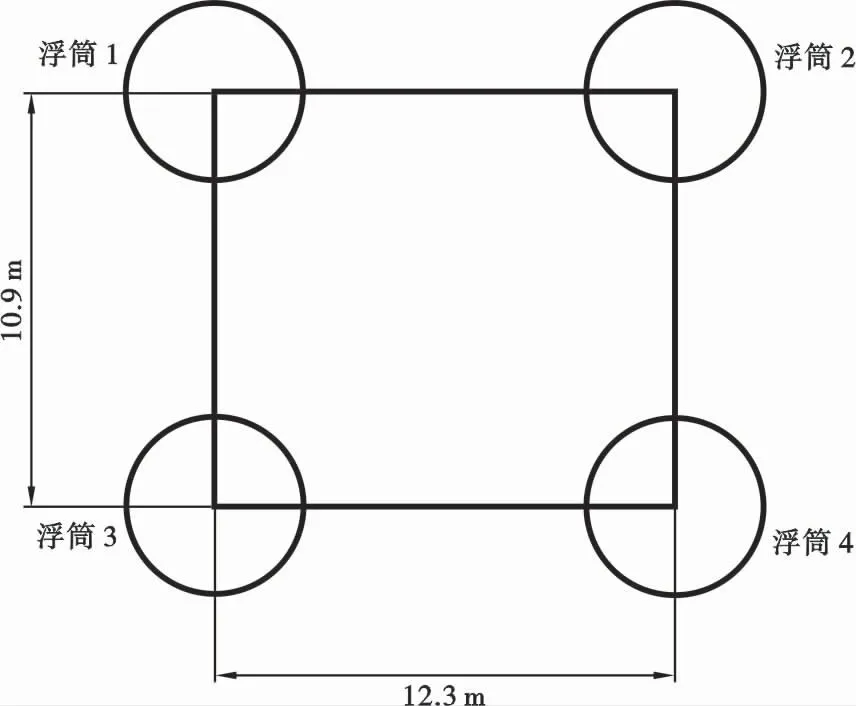
图3 管汇系统的主要尺寸Fig.3 Main manifold dimensions

表1 管汇系统的主要参数Table1 Main parameters of manifold system
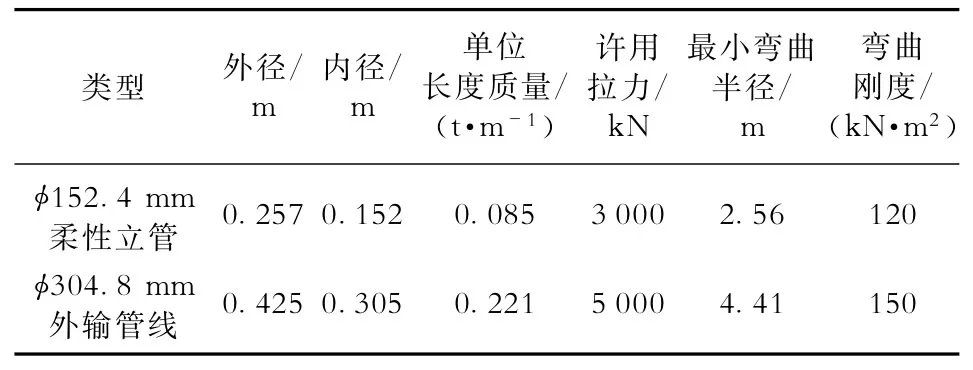
表2 柔性立管和外输管线主要参数Table2 Main parameters of flexible vertical pipe and external pipeline
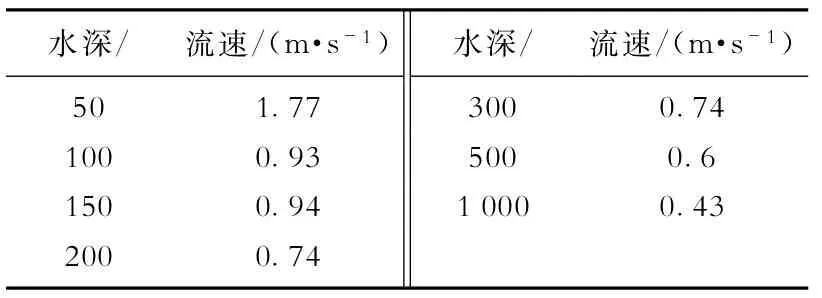
表3 百年一遇海况参数Table3 Once-in-a-century sea condition parameters
2.4 悬链线参数设计
由于输送极端油气密度会导致管汇产生不可忽略的升沉运动,因此本文提出一种针对这种运动方式下的设计思路:首先确定管汇悬浮范围和管线在最低位的悬挂角,当管线提升到最高位时,管线在自然悬挂时海床的触地点位置与管线悬跨长度存在唯一解。根据设计思路,确定悬浮范围为50~100 m,最低位悬挂角为0°,当管线被提升到最高位100 m时(图4),触地点位置与悬跨长度关系为(122 m,168 m)。可以看出,最低位悬挂角的改变对应触地点位置与悬跨长度的相应改变。当最低位悬挂角分别为0°、9°和21°时,对应关系值分别为(122 m,168 m)、(171 m,207 m)和(250 m,276 m)。管线悬挂角数值越大,其对管汇提供的水平拉力也会越多,因此选择悬挂角最小的关系值(122 m,168 m)来设置安装在管汇一侧的外输管线,以减小对管汇偏移的影响。若将锚点直接设置在触地点位置,当管汇悬浮在较高位置时,海流作用产生的偏移会使管线全部拉起,造成结果不准确,因此模拟中适当延长了锚点的位置。
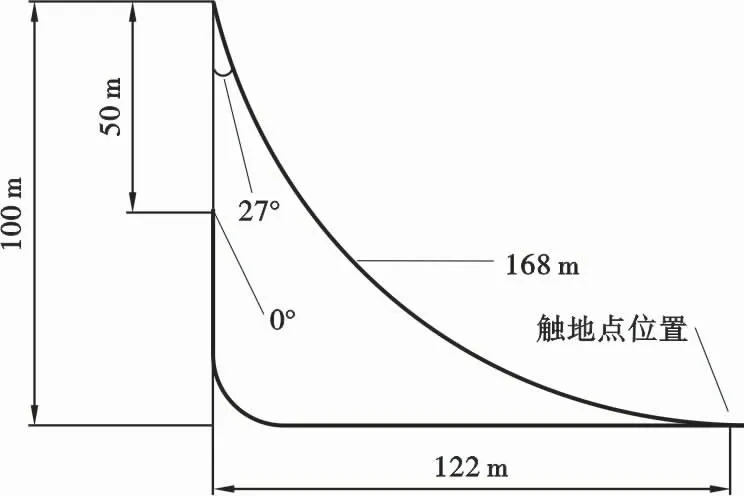
图4 触地点位置和悬跨长度关系示意图Fig.4 Schematic diagram of contact location and suspension span length
2.5 许用浮筒质量范围确定
输送不同密度油气和调节浮筒质量都会使管汇悬浮高度发生变化。为了满足管汇在输送不同密度油气时均悬浮在50~100 m的条件,需要确定许用浮筒质量范围。参考水下生产系统在停产或水压试验的条件,本文选取4个典型密度和3组触地点位置与悬跨长度的数据,模拟计算不同密度油气对应的浮筒许用质量范围(表4)。从表4可以看出,在确定的触地点位置与悬跨长度关系下,不同密度对应的浮筒许用质量范围存在交集,若在该交集内选择浮筒质量,则可保障管汇悬浮在50~100 m内(此时该交集即为浮筒许用质量范围)。在(122 m,168 m)、(171 m,207 m)和(250 m,276 m)的触地点位置与悬跨长度关系下,浮筒许用质量范围分别为72.95~76.67 t,70.98~76.25 t和67.43~75.13 t。
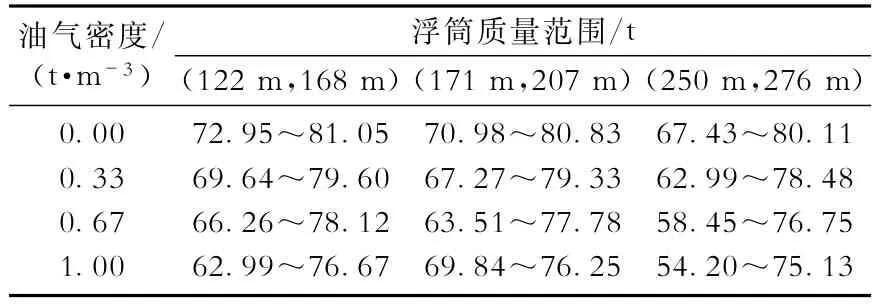
表4 不同油气密度下浮筒许用质量范围Table4 Allowable mass range of buoy under different oil and gas densities
3 模拟结果分析
3.1 管汇主要参数变化规律分析
根据表4的浮筒许用质量范围及对应的3组触地点位置与悬跨长度关系,模拟得到在0.00 t/m3和1.00 t/m32种极端油气密度条件下管汇与管线稳定性主要参数变化规律,如图5、6所示。
根据图5a可知,管汇悬浮高度随浮筒质量增加而降低,但在不同的浮筒质量下,管汇悬浮范围均在30 m左右。根据图5b可知,管汇在极端油气密度下的偏移量变化范围随浮筒质量增加而逐渐变大,原因是随着浮筒质量增加,相对于柔性立管,外输管线对管汇水平拉力的影响越来越大。由于图5a中的悬浮范围小于50 m,可根据悬链线参数设计思路选择图5a的悬浮范围与最低位的0°悬挂角对外输管线悬跨长度关系进行优选,该优选可使悬跨长度趋于合理,从而降低管汇偏移量的影响,得到外输管线悬跨长度与浮筒质量关系,如图7所示。根据图5c可知,管汇整体偏转角度较大,但在极端油气密度下的偏转范围整体较小,因此在保证悬浮高度不变的情况下,以保持浮筒的平均质量而改变两边浮筒质量差的方式平衡外输管线对管汇偏转的影响,调节后的管汇在输送极端油气密度时偏转角度较小,对应的浮筒单个质量与平均质量关系如图8所示。
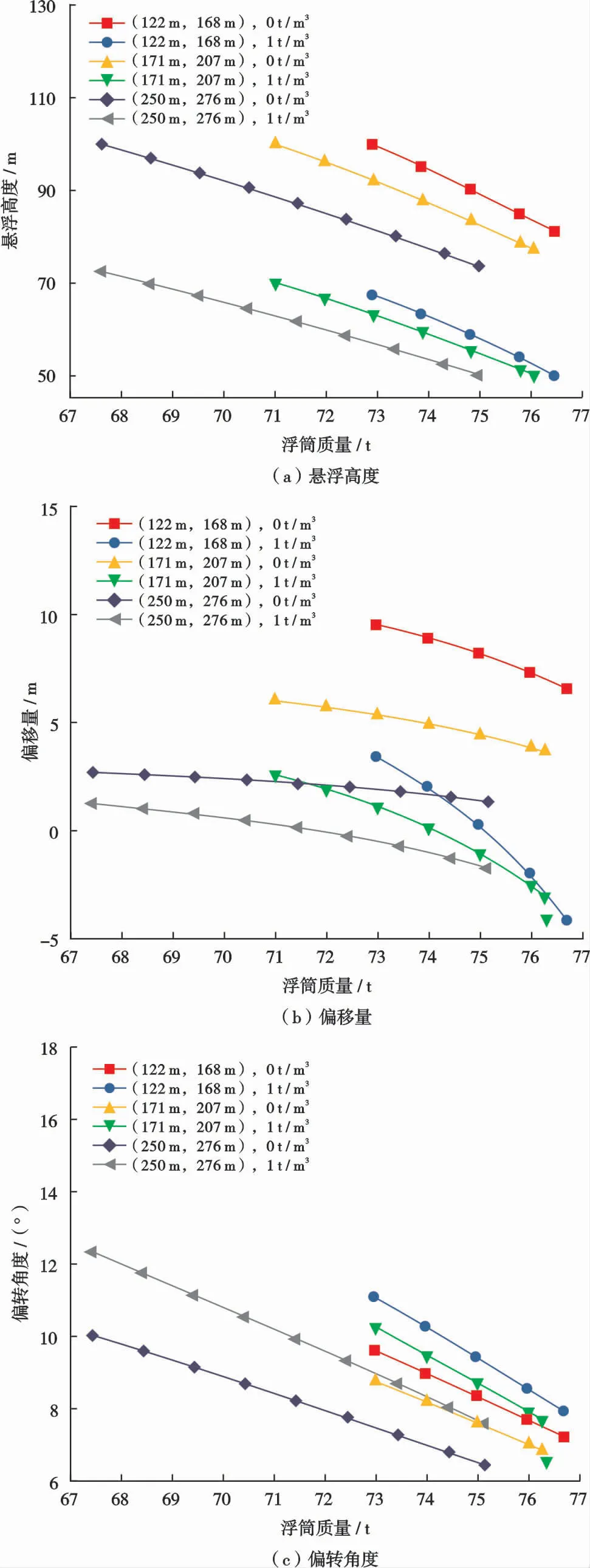
图5 管汇稳定性主要参数变化规律Fig.5 Changes of main parameters of manifold stability
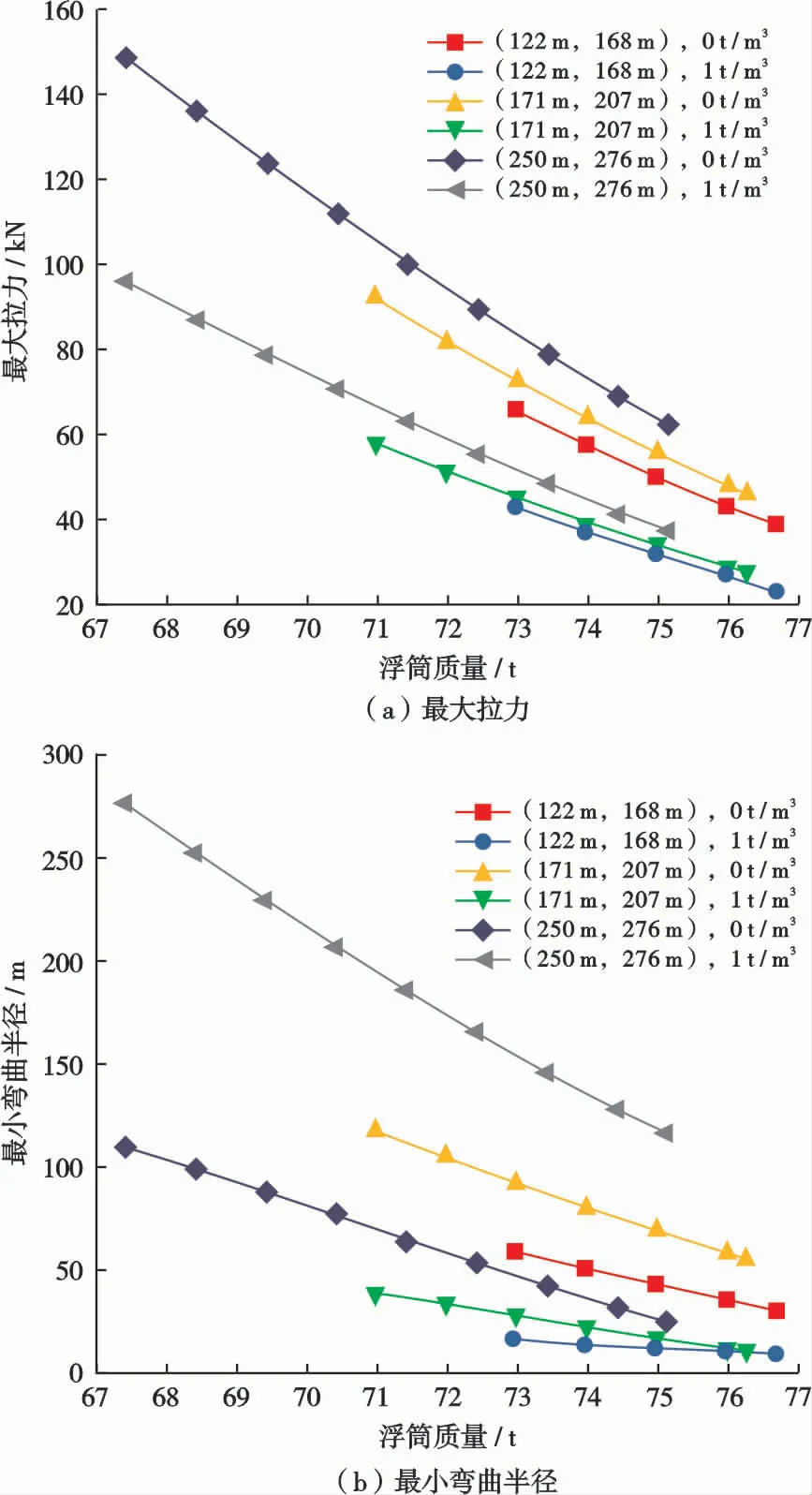
图6 管线稳定性主要参数变化规律Fig.6 Changes of main parameters of pipeline stability
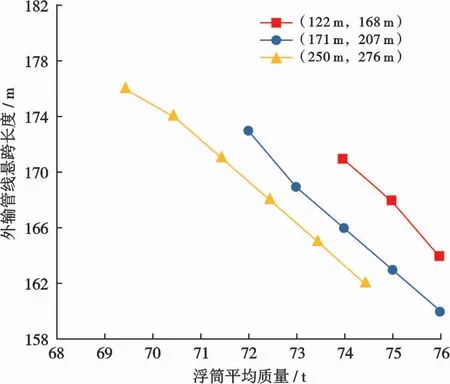
图7 外输管线悬跨长度与浮筒平均质量关系Fig.7 Relation between suspension span length of external pipeline and average mass of buoy
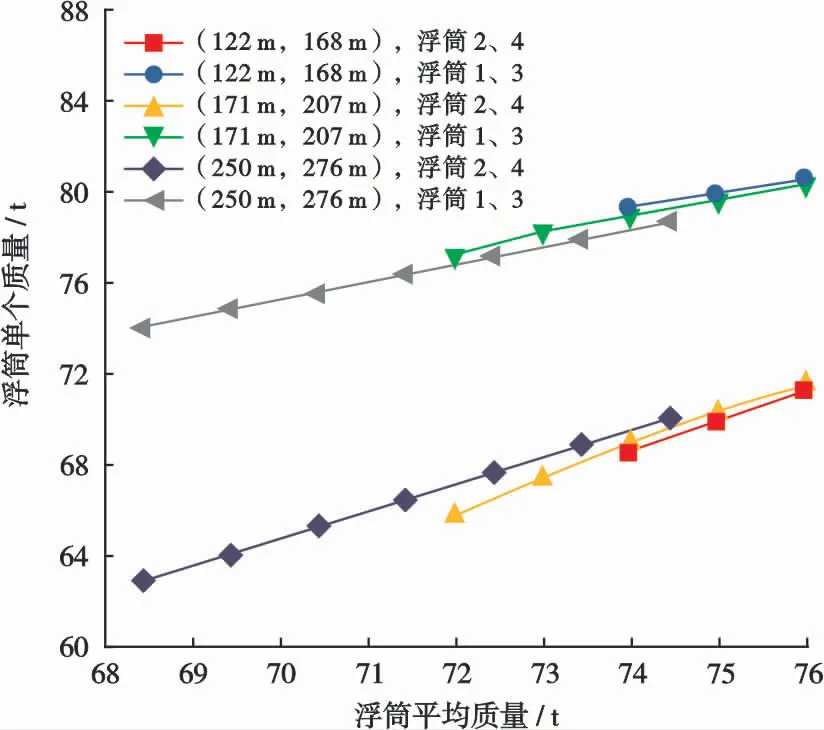
图8 浮筒单个质量与平均质量关系Fig.8 Relations between single mass and average mass of buoy
根据图6可知,最大张力和最小弯曲半径值随浮筒质量增大而减小,但最大张力值远小于许用张力,最小弯曲半径值在合理范围内。但为防止管线触地点处发生较大弯曲,应避免浮筒质量较大的情况。
3.2 优选后管汇主要参数变化规律分析
管汇悬浮在最低位时管线拉力较小,海流对管汇扰动较大,弯曲半径值较小。管汇悬浮在最高位时管线拉力相对较大,安装难度增加。因此,这里只考虑管汇在最低位与最高位之间的管汇参数变化情况。由于调节浮筒质量差值并未改变对应4个浮筒的平均质量,因此图9和图10的横坐标用浮筒平均质量来表示。根据图7和图8的优选结果重新建立对应模型,得到极端油气密度下管汇稳定性主要参数的变化规律,如图9所示。
对比优选前后管汇稳定性主要参数的变化规律(图5、9),可以发现:改变外输管线悬跨长度与浮筒质量差值,管汇的悬浮范围变化不明显;改变输油管悬跨长度可使偏移量处在合理区间内,但无法消除偏移量;改变浮筒质量差值,可明显降低管汇的偏转程度,且随着浮筒平均质量的增加,偏转角度范围逐渐降低,最大偏转角度不超过2°,符合管汇在不同油气密度下的输送要求。
3.3 海流作用下管汇偏移量变化规律分析
模拟油气密度为0 t/m3时管汇受到0°、90°、180°和270°方向的百年一遇海流时的管汇偏移量,结果如图10所示。可以看出,随着浮筒平均质量增加和悬挂角的减小,管线张力的水平分量减小,在海流作用下,管汇的偏移量增大。最大偏移范围发生在(122 m,168 m)处,当浮筒平均质量为76 t时,对应的X轴偏移范围约为6.4 m,Y轴偏移范围约为6.0 m。
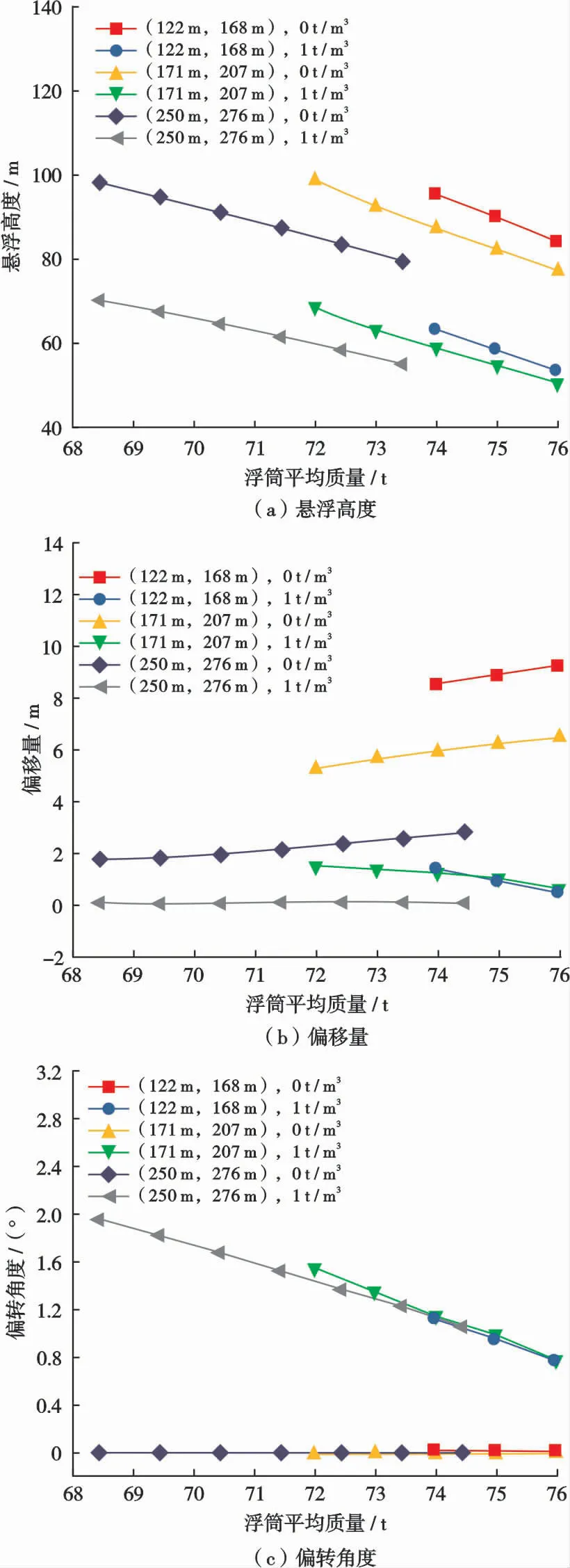
图9 优选后的管汇稳定性主要参数变化规律Fig.9 Variation rules of main parameters of manifold stability after optimization
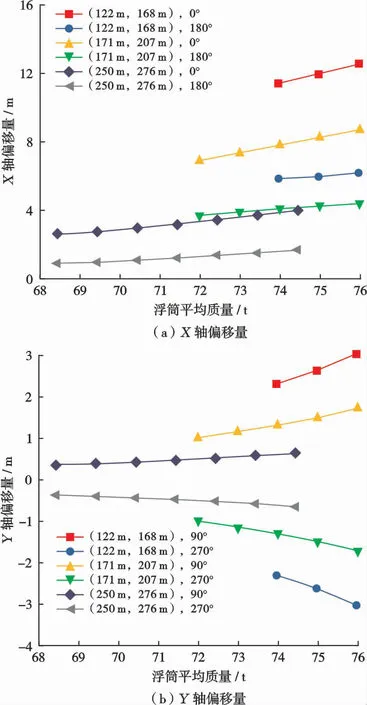
图10 百年一遇海流作用下管汇偏移量Fig.10 Manifold offset under the action of once-in-acentury ocean current
4 结论
1)本文利用OracleFlex软件建立了水下悬浮丛式管汇概念模型,分析了浮筒许用质量范围内管汇与管线稳定性主要参数的变化规律,认为管汇偏移量与偏转角度不满足管汇工作稳定性的要求,管线最大拉力和最小弯曲半径在合理范围内。
2)通过优选外输管线悬跨长度与调节浮筒质量差可以得到管汇稳定性主要参数的变化规律,认为优选外输管线悬跨长度可使管汇偏移量趋于合理,调节浮筒质量差可以使管汇在输送不同密度油气密度时不发生较大偏转;降低浮筒平均质量可使管汇悬浮在较高位置,此时柔性立管有效张力较大,抗海流能力较强,管汇稳定性较高,可满足管汇稳定系泊的要求,实现水下悬浮丛式管汇的全空间布局方案。
