基于Polar码改进的RLCE公钥加密方案

李喆，韩益亮,2，李鱼

（1.武警工程大学密码工程学院，陕西 西安 710086；2.武警部队密码与信息安全保密重点实验室，陕西 西安 710086）

1 引言

量子计算机技术的飞速发展，将深刻影响当前和未来的社会。银行交易、无人驾驶、保密通信等与人们息息相关的各方面的安全性依赖于密码学。Shor[1]提出的量子算法，极大影响了基于大整数分解困难问题的RSA等[2]公钥密码方案；Grover[3]提出的量子算法，极大影响了AES等[4]对称密码方案。Shor算法和Grover算法的提出给经典密码方案的安全性带来严峻的挑战。

为了应对量子计算机对基于经典数学困难问题的密码方案的威胁，各国纷纷寻求能够抵抗量子计算机攻击的新型密码方案，即后量子密码或抗量子密码（PQC，post-quantum cryptography）。美国NIST（National Institute of Standards and Technology）在2012年启动后量子算法的标准化项目，2016年面向全球征集后量子密码算法，2019年征集算法完成第二轮遴选[5]。欧洲电信标准化协会（ETSI，European Telecommunications Standards Institute）开展量子安全会议以此推动后量子密码算法的征集工作，逐步推进全球后量子密码算法项目PQCRYPTO和后量子密码算法应用项目SAFCRYPT[6]。在以上各国或地区制定后量子密码算法标准的同时，我国也同步推进后量子密码算法设计竞赛活动，制定后量子算法标准，截至2019年，后量子密码标准化已进入第二轮评选。后量子密码方案主要包括5种[7]，5种密码方案各有其独特的应用范围。目前，基于编码的方案和基于格的方案成为研究的热点。基于编码的密码方案相较于其他类型的后量子密码方案，更适合构造加密方案，在后量子密码加密方案中，基于编码的加密方案具有良好的研究前景。

基于编码的密码方案最早可追溯到1978年的McEliece方案[8]，该方案最初使用Goppa码作为底层编码，该方案在适当的参数选择下仍然是安全的，并进入PQC第二轮征集算法。基于Goppa码的McEliece方案的安全性是基于一般线性码的译码困难问题，可以规约到NPC（nondeterministic polynomial complete）问题，具有抵抗量子计算机攻击的特点，众多密码学者开始研究此方案。1986年，Niederreiter[9]利用McEliece方案的对偶形式构造了一种加密方案，即Niederreiter方案。McEliece方案和Niederreiter方案均存在密钥尺寸过大的缺点，在实际场景中难以应用。针对McEliece方案实用化差的特点，密码学者通过利用其他结构更加紧凑的编码作为底层编码以减小密钥尺寸，然而构造的变形方案存在安全性问题，易受到结构化攻击[10]。如何在保证密码方案安全性的基础上，同时构造较小密钥尺寸的密码方案成为基于编码的密码方案亟待解决的问题。

2016年，Wang[11]通过在生成矩阵的每一列中插入随机列构造了线性随机码公钥加密（RLCE，random linear code encryption）方案，该方案进入PQC第一轮征集算法评选。不同于其他利用结构紧凑的编码的密码方案，该方案不依赖于任何底层编码的结构。RLCE方案通过插入随机列使方案达到随机性，同时方案的安全性依赖于线性随机码译码的NPC问题，避免了因底层编码结构引入的结构化攻击。2017年，Wang[12]针对RLCE方案存在的潜在攻击，进一步研究RLCE方案的填充方法，改进后的RLCE方案减小了密钥尺寸，提高了加解密性能，达到了IND-CCA2安全性。Matthews[13]在2019年CBC（Code-Based Cryptography）会议上提出用Hermitian（埃尔米特）码作为RLCE方案的底层编码，在128 bit安全级别和256 bit安全级别的情况下，相较于GRSRLCE加密方案、HermitianRLCE加密方案的公钥尺寸分别减少了80%、72%。Liu等[14]在2019年A2C（Algebra,Codes and Cryptology）会议上提出利用Polar码作为RLCE方案的底层编码，通过利用Polar码的极化性质，降低了加解密复杂度，在正确参数选择下，可以达到预期的安全级别，同时密钥尺寸保持在合理的范围内。然而，Liu在文献[14]提出的方案没有考虑语义安全，易受到自适应选择密文攻击。

本文在RLCE方案和PolarRLCE方案的基础上，利用Polar码的极化性质，通过RLCEspad消息填充，提出一种具有IND-CCA2安全的基于Polar码改进的RLCE公钥加密方案。改进的方案利用Arikan[15]提出的Polar码作为底层编码，在信息比特列中插入随机列，选择随机非奇异矩阵对随机列进行混合，选择等价类较多的置换矩阵对生成矩阵进行扰乱，利用消息填充的方法，使用普通编码对密文进行编码。改进后的方案没有改变RLCE方案的结构，仍然具有随机性，可以抵抗McEliece方案存在的结构化攻击。此外，本文采用系统矩阵的形式，对部分私钥进行预计算，减少了密钥存储空间。

2 基础知识

2.1 Polar码编码理论

根据Shannon阐述的信道容量概念，Polar码是至今唯一可以在理论上证明达到这一容量的编码。Polar码具有良好的性能，加解密复杂度低，计算复杂度为O(nlogn)。Polar码由于其独特的极化性质、较低的加解密复杂度，成为众多通信领域学者和密码领域学者研究的焦点。目前，利用Polar码在物理层的极化性质，许多学者在信息安全保密领域取得突破[16]。华为利用Polar码信道容量大、传输速率高、安全性强的优点，将Polar码作为5G时代无线通信的编码[17]。

Polar码相较于Goppa码具有更好的纠错能力，较低的加解密复杂度，较多的等价类码族。拥有以上优点的Polar码应用到编码密码方案中，将具有合理的密钥尺寸，更加适合构造基于Polar码的加密方案，基于Polar码的加密方案具有良好的应用前景。Shrestha等[18]将Polar码应用到密码方案中。随着Polar码理论的进一步发展，Hooshmand等[19]进一步研究Polar码在密码方案中的应用，完善基于Polar码的密码方案。

定义1对称信道

Polar码可以实现任何二进制输入的离散无记忆性信道的（B-DMC，binary input discrete memoryless channel）容量，如二进制擦除信道（BEC）和二进制对称信道（BSC）。下面阐述二进制对称信道相关定义。定义X是输入符号集，Y是输出符号集，转移概率为W(y|x)，x∈X，y∈Y。信道W经过N次极化后，信道可以表示为WN，则信道WN：XN→YN的转移概率为

关于B-DMC的性能，可以通过两个参数进行评价：对称容量I(W)和巴氏参数Z(W)。下面对两个参数相关定义进行阐述。

（1）对称容量（symmetric capacity）

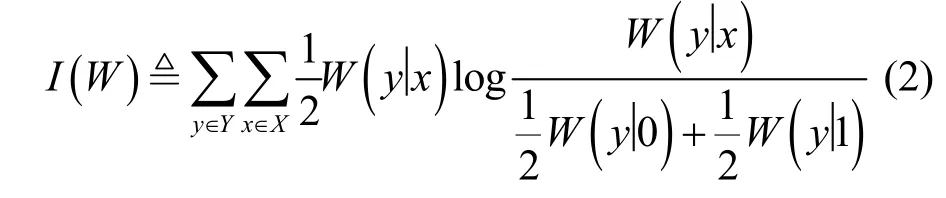
（2）巴氏参数（Bhattacharyya parameter）

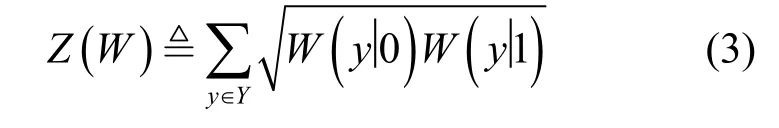
I(W)∈[0,1]用于评估信道速率，Z(W)∈[0,1]用于评估信道可靠性。I(W)与Z(W)具有如下的关系：当且仅当Z(W)≈0时，I(W)≈1；当且仅当Z(W)≈1时，I(W)≈0。

定义2信道极化

信道极化分为两个阶段：信道融合阶段（channel combining）和信道分化（channel splitting）阶段。

（1）信道融合阶段描述

步骤1WN:XN→YN，N为2的n次幂N=2n，n≥0。其中，X表示输入符号集合，Y表示输出符号集合，WN表示信道W的N次使用后的信道。

步骤2YN，u1N∈XN,GN为N维生成矩阵,N=2n。其中，为原始比特输入序列；为通过生成矩阵编码后的比特序列。

（2）信道分化阶段描述

步骤1将信道融合构成的复合信道WN分裂为N个二进制输入的坐标信道。如下所示。

步骤2。

定义3极化码编码

图1 极化编码步骤Figure 1 Polar coding steps

（1）极化信道可靠性估计

（2）比特混合

可靠性较高的K个分裂子信道传输信息比特序列，而可靠性较低的分裂子信道传输冻结比特。通过比特混合后，输出的比特为编码的最初比特。对于BEC来说，选择巴氏参数最小的K个子信道传输信息比特。

（3）构造生成矩阵

首先定义Kronecker 矩阵乘法为

定义矩阵F为，则生成矩阵，其中表示对矩阵F的n次克罗内克积，。BN是比特反转排序矩阵，用来对比特重排操作。BN的递归式定义为

其中，I2为2维单位矩阵，B2=I2；RN为置换矩阵，用来分离输入序列中的奇偶元素。

2.2 RLCE加密方案

（1）RLCE密钥生成过程如算法1所示。

算法1RLCE密钥生成

输入(n,k,d,t,w),n,k,d,t>0，w∈{1,2,…,n},k+1≥d≥2t+1。

输出公钥Gpub，私钥(S,G1,P,A)。

1)选择长度为n，维度为k的k×n生成矩阵G。

2)随机选择w个k×1的列向量r1,r2,…,rw，将w个列向量随机插入生成矩阵G中，得到k×(n+w)的生成矩阵G1，G1=(g1,…,gn-w,gn-w+1,r1,…gn,rw)。

3)为了混合选择的列，选择w个2×2随机非奇异矩阵A1,A2,…,AW。

4)定义A=[1,…1,A1,A2,…,AW]是(n+w)×(n+w)的非奇异矩阵。

5)S为k×k的非奇异矩阵，P为(n+)w×(n+w)的置换矩阵。

6)输出k×(n+w)的公钥，私钥(S,G1,A,P)。

（2）RLCE加密过程如算法2所示。

算法2RLCE加密

输入公钥Gpub，明文，随机错误向量。

输出密文。

（3）RLCE解密过程如算法3所示。

算法3RLCE解密

输入密文，私钥(S,G1,A,P)。

输出明文，译码错误标识⊥。

2)从长度为n+w的向量中删除w个列向量，得到长度为n的c′=(c1′,c2′,…,cn′-w+1,cn′-w+3,cn′-w+5,…,cn′+w-1)。

3)c′=。

4)利用译码算法，计算m′=mS，m=m′S-1。

5)计算汉明重量w=wt(c-mG1)，假如w≤t，输出明文m；否则，输出⊥。

2.3 信息编码

为了抵抗编码密码方案存在的已知攻击，可以通过消息编码（消息填充）的方法保证密码方案的安全性。通常，在密文中有3种方法可以对消息进行编码[12]。

（1）基本编码（basic encoding）

（2）普通编码（medium encoding）

除了基本编码之外，更多的消息被编码在e的非零项中。在这种情况下，可以在每个密文中编码长度为mLen=m(k+t)位信息。严格地说，因为，编码信息小于m(k+t)位。

（3）高级编码（advanced encoding）

除了普通编码，更多的消息被编码在e的非零项中。非零e共有种可能，在这种情况下，可以在每个密文中编码长度为mLen=的信息。

接下来概述常见的5种消息填充类型。

1)Pointcheval padding[20]

2)Fujisak-Okamato padding[21]

3)Kobara-Imai′sα-padding[22]

4)Kobara-Imai′sβ-padding

5)Kobara-Imai’sγ-padding

其中，H1、H2是随机谕言机模型（也可以是伪随机位生成器或者哈希函数）输出固定长度的伪随机比特串；1r、2r是随机选择的适当长度的比特串。

3 本文的加密方案

3.1 改进的RLCE公钥加密方案

本文提出的基于Polar码改进的RLCE公钥加密方案是在Wang提出的RLCE方案和Liu提出的基于Polar码的RLCE方案的基础上，针对Liu提出的PolarRLCE方案密钥尺寸较大且不具有IND-CCA2安全的缺点，提出的一种改进方案。本文利用Polar码的极化性质和译码复杂度低的优点，将Polar码作为RLCE方案的底层编码，改进后的方案采用Wang的RLCE方案的结构，没有改变RLCE方案的具体形式。将Wang的RLCE方案的IND-CCA2形式化安全证明应用到Liu的基于Polar码的编码方案中，对PolarRLCE方案进行消息填充，对每个密文进行语义安全普通编码，并将公钥矩阵转化为系统矩阵，对部分私钥采用预计算[23]，以减少密钥存储空间。本文方案和RLCE方案类似，包括密钥生成（polarRLCE.KeySetup）、加密（polarRLCE.Enc）、解密（polarRLCE.Dec）。

（1）密钥生成

密钥生成过程如下。

1)参数选择：(n,k,d,t,w),n,k,d,t>0，w∈{1,2…,n},k+1≥d≥2t+1。

2)G：长度为n，维度为k的Polar码的k×n生成矩阵，译码算法可以纠出至少t个错误。

3)G1：长度为n+w，维度为k的Polar码的k×(n+w)的生成矩阵，可以将随机选择的w个k×1的列向量r1,r2,…,rw随机插入生成矩阵G得到G1=(g1,…,gn-w,gn-w+1,r1,…gn,rw)。

4)A：(n+w)×(n+w)的非奇异矩阵

5)S：k×k阶的非奇异矩阵。

6)P：(n+w)×(n+w)阶的置换矩阵。

7)Gpub：k×(n+w)的公钥Gpub=SG1AP。

公钥Gpub=SG1AP，私钥 (S,G1,A,P)。

（2）加密

发送方对明文进行加密过程如下。

2)发送方利用接收方的公钥pubG对明文m进行加密，得到密文。

（3）解密

接收方对密文进行解密过程如下。

1)接收方收到密文c，利用自己的私钥，对密文c右乘P-1A-1，得到

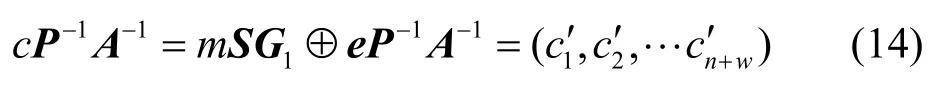
2)接收方从长度为n+w的向量(c1′,c2′,…)中删除w个冻结比特列，得到长度为n的向量，c′=（其中，e′=eP-1A-1），此时的wH(e′)≤t。

3)接收方利用Polar码的SC译码算法，对c′进行译码，得到明文m。

4)接收方计算汉明重量wt=wt(c-mG1)，假如wt≤t，输出明文m；否则，输出⊥。

3.2 将公钥矩阵转换为系统矩阵

令mSG1=(d1,…dn)，=(d1,d2,…,⊥,…,dn,)P是长度为n+w的向量。

对于每个i＜k，当j＜n-w，di′=dj，令mi=dj，当m=(m1,…mk)。

IR={i:mi}（mi译码成功）；={1,…,k}IR（im译码失败）。

P为置换矩阵，恢复出在mP中前k-u个mi(i∈IR)信息。通过式(15)计算得到

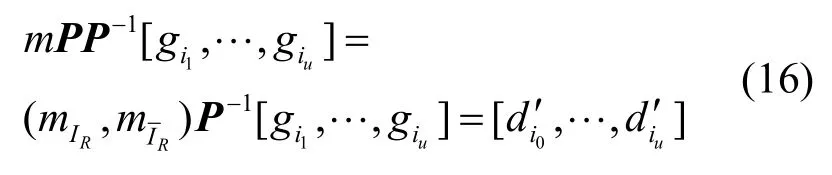
其中，mIR是在IR带有索引的消息列表。

可以预计算W-1。

通过将公钥矩阵转换为系统矩阵，可以把V,W-1作为私钥存储，不再存储私钥S，以降低密钥存储空间。

3.3 消息填充

Liu提出的PolarRLCE方案不具有IND-CCA2安全，本文采用Wang提出的适合加密较短信息的RLCEspad消息填充的方法，使改进的方案达到IND-CCA2安全。对信息进行填充后，信息转化为RLCE方案中的信息位或其他信息，采用普通编码，填充的信息可以被编码在e的非零项中。

首先明确相关变量定义RLCEspad (mLen,k1,k2,k3,t,m,r)

（2）H1,H2,H3是随机谕言机模型，可以分别将任意长度的二进制比特串转化为长度为k2，k1+k2，k3字节的输出比特串。

（3）m∈{0,1}8k1是需要填充的信息，当r1∈是随机选择的二进制比特串。

RLCE填充过程如算法4所示。

算法4 RLCEspad

输入mLen,t,m,r,H1,H2,H3。

输出(y1,e1),c。

1)计算v=8(k1+k2+k3)-mLen。

4)将y转化为(y1,e1)∈，输出(y1,e1)，得到密文c=y1G+e。

4 安全性分析

（1）穷举攻击

穷举攻击是通过一一穷举可能存在的正确私钥，从而恢复明文，达到攻击密码方案的目的。通过采取系统矩阵的形式，改进后的私钥为(V,W-1,G1,A,P)。本文采用Polar码作为方案的底层编码，其置换矩阵P等价类码族较多，攻击者通过穷举攻击难以在多项式时间内找到正确的P，对密文难以进行操作，，无法恢复出正确的明文。此外，根据Liu方案选择的参数，攻击者通过穷举的方法找到其他4类密钥也是不可行的。所以，穷举攻击不会对本文方案的安全性造成影响。

（2）密钥恢复攻击

密钥恢复攻击的基本思想是：从公钥Gpub恢复出正确的私钥。密钥恢复攻击是一种结构攻击，通常是针对特定的编码，如QC-LDPC码、GRS码等。本文提出的方案插入了随机列，同时采用2×2随机非奇异矩阵A对插入的随机列进行混合，私钥的结构被打乱。混合之后又随机从长度为n+w密文中删除w列冻结比特列，由于攻击者无法知道Polar码的极化性质，进一步增加了私钥结构的复杂度，攻击者在多项式时间内通过公钥难以恢复出正确的私钥结构。Bardet等[24]针对Polar码提出一种确定最小权重的攻击，解决了极化码相对于递减单项式码的等价问题。本文方案插入的随机列扰乱了生成矩阵的原有编码结构，所以文献[24]不会影响本文方案的安全性。因为Polar码的结构与汉明循环码、GRS码和RM码结构不同，针对底层编码为循环码、GRS码和RM码的结构化攻击，不会威胁本文方案的安全性。

（3）信息集译码攻击

信息集译码攻击是对McEliece编码方案最有效的攻击，在所有已知的攻击中，基于信息集译码的攻击拥有最低的计算复杂度。Stern[25]首先提出对McEliece方案的信息集译码攻击，此后，攻击者为了提高对编码方案攻击的有效性，提出许多改进的高效率的信息集译码攻击[26]。信息集译码攻击不是利用编码的底层结构对密码方案进行攻击的，而是利用搜索信息集的方法达到攻击的目的。此外，信息集译码攻击的工作因子随错误向量的增加而增加。对于RLCE方案，信息集译码攻击寻找的是公钥Gpub的列数，而不是私钥G1的列数。从含有t个错误的n+w位密文中随机选择k位，构成xk，从错误向量e中选择对应位置的k位构成ek，从Gpub选取对应的列构成k×k矩阵。如果选取的ek不含有错误的比特，即ek=0，攻击者很容易恢复出明文m。

对于从RLCE方案公钥中随机选择的k列，密文在这些位置上不包含错误的概率为

本文通过插入w个随机列，增加了寻找选取的错误向量ek无差错位置的困难性。给定适当的参数，攻击者通过信息集译码攻击获取明文m是极其困难的，所以，本文通过插入随机列保证了密码方案不受信息集译码攻击的影响。

（4）反应攻击

反应攻击是攻击者通过修改少量的密文c，将修改后的密文发送给接收方，观察接收方是否可以正确译码。对于给定的密文c，攻击者随机选择位置i，在位置i添加错误，将添加错误的密文c发送给接收方，观测接收方是否可以正确译码。如果接收方可以正确译码，说明攻击者在位置i添加了错误；假如接收方译码失败，说明攻击者在位置i没有添加错误。重复进行上述操作，直到攻击者获得k个无差错位。本文通过插入w个随机列，消息填充，可以抵抗反应攻击。Liu提出的基于Polar码的RLCE方案没有考虑到反应攻击，本文对可能存在的反应攻击加以分析发现，不同于底层编码为汉明循环码的密码方案，通过消息填充的方法，本文方案可以抵抗可能存在的反应攻击。

5 IND-CCA2安全性

本文方案采用系统矩阵对明文m进行加密，使用这种方法加密明文，可能会导致方案IND-CCA2的安全性降低。Liu提出的基于Polar码的RLCE方案不具有语义安全，并举例说明了一种相关性攻击的情况：对同一明文m进行两次加密得到两个不同的密文，可以将两个不同的密文进行对比分析来找出原始的消息。根据上述阐述的消息填充方法，本文采用RLCEspad填充方法，对每个密文进行普通编码，使部分消息被编码在错误向量e非零项中。发送方在发送明文m之前，通过3个随机谕言机模型H1,H2,H3将信息打乱，将部分消息编码在错误向量e非零项中，然后将编码后的消息发送给发送方。攻击者为了获取明文m，攻击填充后的密码方案，困难性等价于基于Goppa码的McEliece原始方案。假设解码RLCE密文是不可区分的，可以使用与文献[12]中类似的证明来保证RLCE-RLCEspad方案可抵御IND-CCA2攻击。所以，本文采用RLCEspad方法进行消息填充后的方案具有语义安全，可以达到IND-CCA2安全。

6 性能分析

下面从公钥尺寸与私钥尺寸两个方面分析本文方案。

（1）公钥尺寸

Gpub的尺寸为k×(n+w)，通过采用系统矩阵，改进后的Gpub的尺寸为k×(n+w-k)。

（2）私钥尺寸

私钥(V,W-1,G1,A,P)，V的尺寸为(k-u)u，W-1的尺寸为u×u，G1的尺寸为k×(n+w)，A的尺寸为(n+w)×(n+w)，P的尺寸为(n+w)×(n+w)。通过预计算W-1的值，改进后的方案不再存储k×k阶的矩阵S，减少了私钥存储空间。

通过表1，分析得到：

1)在相同的比特安全级别，本文方案的公钥尺寸和Liu方案一样，但本文方案具有IND-CCA2安全性，且本文对部分私钥采用预计算的方法，可以明显减少私钥存储空间；

2)在相同的比特安全级别，本文基于Polar码的加密方案公钥尺寸最小，在128 bit安全级别，本文方案相较于HermitianRLCE方案、GRSRLCE方案和GoppaMcEliece方案公钥尺寸分别减少了4%、46.5%、47.9%。

表1 基于编码的RLCE加密方案公钥尺寸的对比Table 1 Comparison of public key Size of RLCE schemes based on encoding

7 结束语

利用Polar码的等价类码族较多、加解密复杂度低的优点，本文在RLCE方案和PolarRLCE加密方案的基础上，利用Polar码作为RLCE加密方案的底层编码，通过采用RLCEspad消息填充的方法，将发送的消息扰乱，提出一种具有IND-CCA2安全的基于Polar码改进的RLCE方案。本文将公钥矩阵转换为系统矩阵，减少了公钥尺寸，对部分私钥进行预计算，采用存储预计算的值代替存储私钥S的值，减小了私钥存储空间。改进后的方案依然采用RLCE方案的结构，经过安全分析，可以抵抗目前已知存在的信息集译码等攻击。将Polar码作为底层编码，相较于基于汉明循环码的方案，本文方案可以抵抗已知存在的结构化等攻击。

Polar码因其独特的极化性质和较低的译码复杂度等优点，日益成为研究的热点。将Polar码应用到基于编码的密码方案中，具有良好的研究前景。在接下来的工作中，可以进一步研究Polar码的加密方案，构造更加适合5G通信环境下的轻量级加密方案。此外，研究RLCE方案的安全性和构造具有IND-CCA2安全的RLCE密钥封装机制，也是未来研究的重点。利用RLCE方案是否可以构造安全高效的签名方案，这个问题值得以后深入研究。