利用“万有引力场的环路定理”推算太阳内部温度
2020-10-21廖偲含鲁同所
廖偲含, 杨 兴, 鲁同所,2, 胡 婧
(1. 西藏大学 理学院,西藏 拉萨 850000;2.中国科学院 上海应用物理研究所,上海 嘉定 201800)
静电环路定理作为电磁学中的关键内容,在静电场中具有非常重要的作用和地位,解决了许多具有对称分布性质的静电学问题.历史上许多例子证明类比推理是科学上行之有效的方法,通过类比方法将静电场环路定理推广引入到经典万有引力场中,对于球对称性的天体,能大大简化积分运算过程,加深对天体内部性质的理解.众所周知,太阳是离地球最近目前唯一可以详细研究的恒星,也是太阳系内最大的天体.太阳是一个“火球”,不断进行着热核聚变反应,堪称是一座无与伦比的巨型物理实验室,热核聚变反应与温度息息相关,核反应区作为太阳内部热核聚变的场所,几乎产生了所有的太阳能量,是地球能量的主要来源,其重要性不言而喻,不仅带来物理知识,还影响科技和生活,其中心是一个高温、高密、高压的区域.但由于太阳内部的物理量无法进行直接观测,近年来不断有学者利用太阳表面观测值[1]和有限的物理知识[2]建立太阳模型,但由于密度函数建立和计算方法等原因的不同,各种太阳模型也存在较大差异,其中Bahcall根据最新研究不断发表各种改正后的标准太阳模型[3].但较为直观的推算太阳内部温度的研究鲜有,在中国知网数据库中检索关键词“太阳内部温度”,发现相关中文文献不超过3篇.因此,笔者利用万有引力场的“环路定理”引入引力势能,根据分段密度分布函数,建立太阳内部粒子和引力势能函数,参照太阳数值解模型[4-5],借助Mathematica数学软件,推算太阳中心温度,得到一种较为合理的太阳内部温度分布结构.
1 引力场的环路定理
根据静电场和万有引力场的相似性,将静电场的电场强度概念引入万有引力场中,推导得到万有引力场强度和万有引力场的“环路定理”,如表1所示.

表1 静电场与万有引力场的对比
比例常数G=6.67×1011N·m2·kg-2为引力常数.
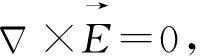
2 非均匀球对称性天体万有引力势能和温度
由静电场的电势能之差类比得到万有引力场的引力势能之差的表达式,如见表2所示.

表2 静电场与万有引力场的对比

图1 球对称性天体示意图

(1)
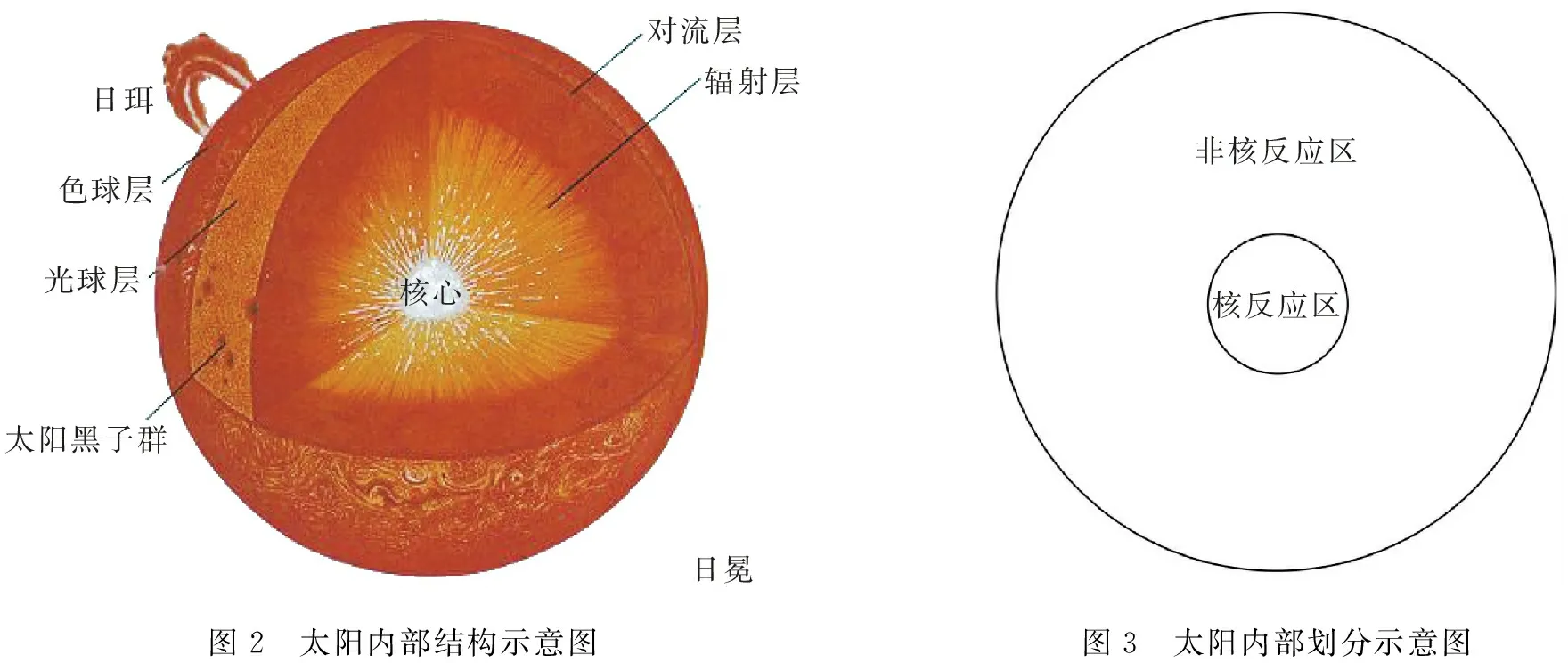
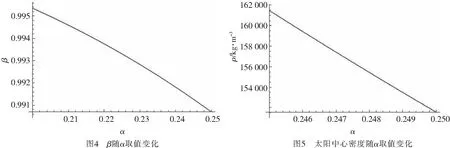
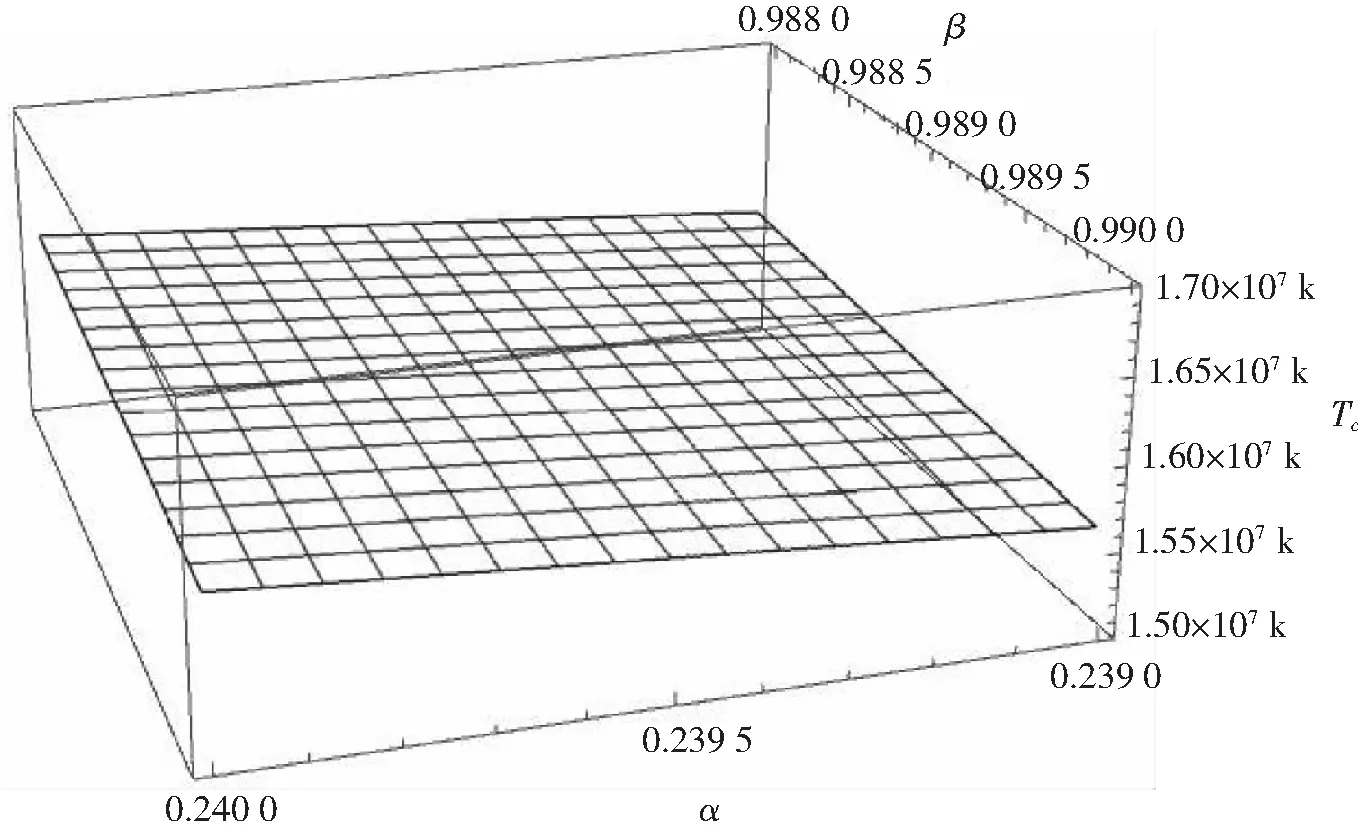
在r至R之间任意取一段微元dr,则对r至R之间的球壳(r (2) 然后把整个球体划分成无数个上述球壳,则整个球体的引力势能看做这无数个球壳的引力势能的叠加 (3) 由维里定理[8],质点的平均平动能为 (4) (5) 则对整个球体,核心温度为 (6) 其中,Nc为整个球体内部粒子数.由式(5)和(6)可知,温度与内部粒子数、引力势能密切相关.由式(2)、(3)和(4)可知引力势能、内部粒子数又都和密度分布密切相关,事实上太阳并不是密度均匀分布的,所以引入ρ-r函数关系. 太阳是一个炽热的气体球,质量为1.989×1030kg,是地球质量的33万倍,半径为6.962 65×108m[1],其密度并不均匀,越靠近中心,密度越大.从太阳中心到边缘可分为核反应区、辐射区、对流区和太阳大气4层,如图2所示.核反应区集中了太阳质量的一半,太阳能量的99%是在这里产生的;辐射区在核反应区外,其密度和温度都很快向外减少,核反应区产生的能量经此区以辐射转移的方式向外传播;对流区密度和温度进一步向外减少,主要以对流方式向外传播能量;太阳大气大致可以分为光球、色球、日冕3个层次,各层的物理性质具有显著差别. 核反应区产生几乎太阳所有的能量,而核反应区以外的区域主要负责将核反应区产生的能量传递出去[2].核反应区能够进行核聚变,非核反应区不能进行核聚变,由此将太阳分为核反应区和非核反应区进行分层计算,如图3所示. 对流层辐射层日珥色球层光球层太阳黑子群日冕核心非核反应区核反应区图2 太阳内部结构示意图图3 太阳内部划分示意图 显然,在太阳中心处,太阳表面的密度相比太阳中心的密度可以忽略,通常假定其为0,所以存在以下边界条件 ρ(0)=ρc, ρ(R)=0. 太阳划分为2个区域,核反应区和非核反应区,如图3所示,设核反应区与非核反应区的分界面半径为a,太阳中心密度ρc和分界面密度ρa定义为 (7) 核反应区(0≤r ρ1=ρ1(r). 在太阳中心附近按照泰勒级数展开 取前3项,为保证密度函数在同一区域光滑,要求ρ1′(0)=0,所以 所以 (8) 非核反应区(a≤r≤R), ρ2=ρ2(r), 在分界面附近按照泰勒级数展开 取前2项,代入边界条件ρ(R)=0=ρ2(a)+ρ2′(a)(R-a)和分界处ρ2(a)=ρa得到 所以 (9) 设 (10) 则边界条件变为 σ(0)=1, σ(1)=0, 密度函数变为: 核反应区(0≤x<α) (11) 非核反应区(α≤x≤1) (12) 5.1 非核反应区的太阳内部引力势能和粒子数对于非核反应区(a≤r≤R),将密度函数ρ1,ρ2代入式(2),得 则在非核反应区引力势能随半径分布函数为 (13) 设 (14) 将式(10)、(12)和(14)代入式(13),则对于非核反应区(a≤x≤1)分布函数变为 (15) 设 (16) 则 (17) (18) (19) 把式(17)、(18)和(19)代入式(15)得 (20) 对于非核反应区(α≤x≤1),将σ2代入式(20)并积分,在x~1个太阳半径范围包含的引力势能与整个太阳引力势能比值为 (21) α~1个太阳半径范围包含的引力势能与整个太阳引力势能比值为 (22) 设 (23) 则将式(10)和(23)代入式(4),粒子分布方程变为 (24) 设 (25) 则 (26) 对于非核反应区(α≤x≤1),将σ2(x)代入式(26)并积分,在x~1个太阳半径范围包含的粒子数与整个太阳粒子数比值为 (27) α~1个太阳半径范围包含的粒子数与整个太阳粒子数比值为 (28) 5.2 核反应区的太阳内部引力势能和粒子数对于核反应区(0≤r≤a),将密度函数ρ1代入式(2) 则在核反应区引力势能随半径分布函数为 (29) 将式(10)、(11)和(14)式代入式(29),则对于核反应区(0≤x≤α)分布函数变为 (30) 设 (31) 把式(16)和(31)代入式(30)得 (32) 对于核反应区(0≤x≤α),将σ1(x)代入式(32)并积分,在x~1个半径范围包含的引力势能与整个太阳引力势能比值为 (33) 对整个太阳来说,在0~1个太阳半径范围包含的引力势能与整个太阳引力势能比值为1, (34) 则 (35) 把式(16)、(17)、(18)、(19)和(31)代入式(34)得 (36) 对于核反应区(0≤x≤α),将σ1(x)代入式(26)并积分,在x~1个太阳半径范围包含的粒子数与整个太阳粒子数比值为 (37) 对整个太阳来说,0~1个太阳半径范围包含的粒子数与整个太阳粒子数比值为1,则 (38) 令 (39) 则 (40) (41) 易得 (42) 5.3 太阳内部的温度由式(25) 得 (43) 由式(39)和(42)可知,将α和β的值代入,即可求得Q值,将Q代入式(43)即得太阳中心密度; 由式(16) 得 (44) 由式(36)可知,将α和β的值代入,即可求得整个太阳的引力势能. 通过太阳光谱分析,太阳的化学元素约有60多种,其中以氢最多.太阳的成分中氢的质量丰度约73.46%,氦约占24.85%,那么太阳内部平均粒子质量[8-9]为 对于整个太阳内部粒子数 (45) 由式(6) 将式(44)和(45)代入式(6)即得太阳内部温度. 核反应区是太阳内部热核聚变的场所,其范围大致从中心到0.20R[10]或0.25R[11],也就是说α的大致范围为0.2≤α≤0.25.如果假定核反应区的氢原子刚好完全电离,区域分界面处的氢原子核的距离可以近似地表示为[2] 氢原子电离的条件可以近似认为是任意2个氢原子核之间的距离刚好是玻尔半径的2倍,即 (46) 其中,a0=5.29×10-11m是氢原子的玻尔半径,mH=1.67×10-27kg是氢原子质量. 将式(7)、(42)和(43)代入式(46)得 (47) 由式(39)、 (47)可知,代入α,利用Mathematica拟合即可求得β值. 如图4所示,在α在0.25取值左右时,β取值在0.99附近.再将α和拟合得到β代入式(39)、(42)和(43),利用Mathematica拟合可以求得太阳中心密度ρc随α取值范围的变化.由上知α的大致范围为0.2≤α≤0.25,目前的研究中一般认为核心在0.25个太阳半径左右,如图5所示.在α在接近0.25取值时,密度在1.56×105kg·m-3左右,而在数值解模型中太阳中心密度为1.56×105kg·m-3[12-13],本文计算与此结果高度吻合. 以ρc=1.56×105kg·m-3为中心密度代入式(43),得到一组对应的α和β值,代入式(36)得到Y1的值,再由式(6)、(44)和(45),利用Mathematica得到中心温度Tc随α和β取值范围的变化,如图6所示. 图6 太阳中心温度随α和β取值变化 当α和β取定一对值,如α=0.239 21,β=0.989时,代入式(6)和(44)求得太阳中心温度Tc=1.58×107K,这与数值解模型中太阳中心温度为1.58×107K[12-13]基本一致. 通过静电场与万有引力场的相似之处,将相关概念引入到万有引力场中,类比得到万有引力场的“环路定理”,求解万有引力势能.根据分界面的性质和太阳内部有无热核反应建立分层密度分布函数,拟合得到与数值模型解比较吻合的中心密度和温度.基于此计算得到太阳中心密度ρc=1.56×105kg·m-3,中心温度Tc=1.58×107K,与太阳内部维持流体静力学平衡而估算得到的1.5×107K相吻合,说明利用万有引力来研究太阳内部状况具有一定的合理性,对于了解太阳内部的物理过程起到了很大的促进作用,同时也为其他恒星的研究提供了新的思路和方法. 基于有无热核反应对太阳内部进行分层,计算中密度函数扮演着重要的角色,但太阳的分层结构非常复杂,并不能进行如此简单的定论.在假定太阳表面密度为0这一过程中,也导致了假定太阳表面温度为0,但事实上并非如此,实际太阳表面的温度为6 000 K[14].从太阳表面至中心的密度变化相对于温度和引力势能较小,因此采用这样的密度分层函数对整个太阳进行研究仍是较为合理的.目前还没有能够完全得到证实的密度分布模型,太阳在不断演化的过程中,各种性质也仍旧是一个谜题.
3 太阳的分层结构
4 太阳的密度分布函数
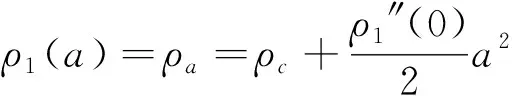
5 太阳内部温度
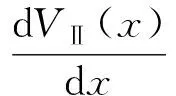
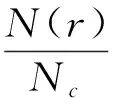
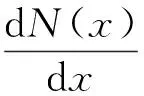
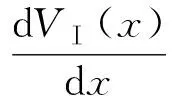
6 结束语
