MBM中基于AMP的多用户检测

宋玮

(北京理工大学 信息与电子学院，北京 100081)

媒介调制(media based modulation,MBM)是一种新兴的索引调制(index modulation,IM)方式[1]，最早由Khandani提出[2]，旨在降低能量损耗和硬件成本，有望成为未来移动通信的关键技术之一. 与空间调制(spatial modulation,SM)[3]类似，MBM上行系统的发射端某个用户在某一时刻仅有一条发射链路有效. SM中的多天线结构导致天线间距占据一定空间从而保证信道的独立性，而MBM的紧凑射频镜面排列方式相较于SM节省了一些空间. 此外，在获得相同的误码率(bit error rate,BER)性能时,MBM方式比SM方式在基站端使用更少的接收天线数，从而减少开销.

对于多用户MBM系统，最大似然(maximum likelihood,ML)检测作为最优检测算法，检测复杂度随用户数量的增加而显著升高，因此不再适用. 低复杂度算法如最小均方(minimum mean square error,MMSE)检测，虽复杂度低于ML检测算法，但检测性能相较ML也有较大不足. 对于MBM自身所具有的稀疏性，多用户检测问题可看作压缩感知(compressive sensing,CS)[4-7]的信号恢复问题，从而进一步提高多用户检测的性能. 目前稀疏信号恢复方法主要有：凸松弛、贪婪迭代和贝叶斯3类方法，其中贝叶斯方法信号恢复精度较高. 置信传播(belief propagation，BP)算法作为一种经典贝叶斯方法，文献[8]在BP算法的基础上，提出了近似消息传递(approximate message passing,AMP)算法. 基于压缩感知稀疏信号重构理论，若观测矩阵满足独立同分布，则可将AMP算法与多用户检测任务相结合，从而在获取较高检测精度的同时进一步减少检测算法的计算复杂度，使得算法更加高效. AMP算法作为一种性能优异的稀疏信号恢复算法，收敛速度较迭代软门限(iterative shrinkage thresholding,IST)[9]算法收敛速度更快. 文献[10-11]中基于AMP的框架提出一种Sep-AMP算法，并利用了SM的独立同分布先验进行多用户检测.

为提高多用户检测的精确度，基于MBM自身的结构稀疏性，提出一种结构化期望最大近似消息传递(structured expectation maximization approximate message passing,Str-EM-AMP)算法. 该算法分为3步：第一步为解耦，该过程和传统AMP算法一致，将接收信号的矢量估计问题解耦成标量估计问题；第二步为去噪，该步骤中综合考虑MBM的结构化稀疏性，估计后验均值和方差估计；第三步为噪声方差估计，该步骤中引入期望最大(expectation maximization,EM)算法实现估计噪声方差. 所提出的算法不仅考虑了每个用户每个射频镜面的自身还考虑了所属该用户的其他射频镜面，从而提升多用户检测性能. 同时，考虑更为实际的场景，算法中包含了噪声方差的估计.

1 系统模型

采用上行大规模MBM MIMO系统，如图1所示. 该系统中基站端配有Nr根接收天线，发射端有U个用户设备，每个用户设备配有一根发射天线和Nt个射频镜面. 每个射频镜面有开启和关闭两种状态，当射频镜面处于开启状态，信号可穿过射频镜面；当射频镜面处于关闭状态，此时射频镜面阻挡信号穿过射频镜面. 因此，Nt个射频镜面可产生2Nt种镜面激活模式(mirror activation pattern,MAP). 表1以Nt=2为例，列举出在此情况下的信息比特序列与MAP映射关系. 发射端每个用户每次采用一种MAP模式，传输的符号来自于调制星座表，例如8移相键控(8 phase shift keying,8PSK)，16正交幅相调制(16 quadrature amplitude modulation,16QAM). 因此，可计算出系统总开销为U(Nt+lbNr).

表1 Nt=2时信息比特序列与MAP映射关系

xu=[0…0xuj0…0]T.

(1)

式中xu为第u个用户的传输信号向量，其维度为Nt×1，xuj∈是xu的第j个元素. 所有U个用户的总传输向量为

(2)

采用的信道为瑞利衰落信道，信道矩阵H=[H1…Hu…HU]∈Nr×UNt，HU∈Nr×Nt. 基站端第i根接收天线收到的接收信号为

(3)

y=Hx+w.

(4)

式中：y=[y1y2…yNr]T；x=[x1x2…xUNt]T；w=[w1w2…wNr]T.

2 Str-EM-AMP算法

AMP算法的物理本质是在大系统极限情况下将原来的矢量估计问题，即式(4)解耦为若干个标量估计问题[12].

(5)

(6)

式中Z(Ri,Σi)为归一化常数.xi的后验估计均值和方差为

(7)

(8)

MBM信号的先验可表示为

(9)

(10)

其中δ(·)为狄拉克δ函数，Iu={(u-1)Nt+1:uNt}. 考虑xu的联合后验分布

(11)

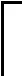
q(xi)=

(13)

(14)

在估计xi后验均值和方差时，不仅考虑了其本身，还考虑了同用户的其他元素，从而更好地利用了MBM的结构化特征. 在利用EM进行噪声方差σ2估计时，主要迭代步骤是在期望步骤E和最大化步骤M

Q(σ2,(σ2)t)=E{lnp(x,y)|y;(σ2)t}.

(15)

(σ2)t=argmaxσ2Q(σ2,(σ2)t).

(16)

式中：(σ2)t表示第t次EM迭代得到的估计结果；E{·|y;(σ2)t}表示已知观测向量y与(σ2)t时的条件期望，联合分布p(x,y)可以写为

(17)

其中

(18)

且za=ΣiAaixi. 由式(17)(18)得

(19)

其中第二项与σ2无关，而第一项为

lnp(y|z)=-Nrln(2π)-

(20)

结合式(19)和(20)可知

lnp(x,y)=-Nrln(σ2)-

(21)

其中Const代表与噪声方差σ2无关的常数项.

将式(19)带入Q(σ2,(σ2)t)，可得

Q(σ2,(σ2)t)=-Nrln(σ2)-

(22)

令Q(θ,θt)对σ2的求导为0，可得噪声方差σ2的更新准则为

(23)

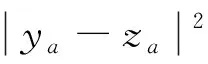
(24)

式中E{za|y;θt}与Var{za|y;θt}分别表示za在已知y时的后验均值和后验方差.za的后验分布为

q(za|y)=

CN(za;E{za|y;(σ2)t}),Var{za|y;(σ2)t}.

(25)

最终噪声方差的估计结果为

(26)

因此，所提出的Str-EM-AMP算法流程如下.

第1步 当a=1,2,…,Nr并且i=1,2，…,UNt：

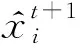
第3步 当=1,2,…,UNt，利用式(26)计算σ2

第4步t=t+1,转到解耦步骤并继续迭代，直到t>Tmax停止迭代

传统MMSE多用户检测算法的计算复杂度为O(Nr(NtU)2+(NtU)3)，Sep-AMP算法的计算复杂度为O(NrNtU+NtU)，本章提出的Str-EM-AMP算法计算复杂度也为O(NrNtU+NtU). 由于Sep-AMP算法和Str-EM-AMP算法中没有矩阵求逆运算，因此这两者的计算复杂度均与Nr，Nt和U呈线性关系.

3 仿真和比较分析

为验证所提出的Str-EM-AMP算法在多用户检测方面的有效性，将其与MMSE算法和Sep-AMP算法进行仿真对比及分析. 实验设置了不同的用户数U，基站天线数Nr，信噪比RSN. 详细实验参数设置情况为：用户数U=16，单个用户射频天线数Nt=4，基站天线数Nr=64，调制方式4QAM. 同时设置Sep-AMP算法和Str-EM-AMP算法所迭代的最大次数Tmax=20，3种算法的BER性能对比如仿真结果图2所示.

由仿真结果图2可知，基于AMP的两种方法明显优于MMSE算法. 同时，在对比Sep-AMP算法与Str-EM-AMP算法时，由于所提出的Str-EM-AMP算法考虑了MBM自身的结构稀疏性，BER性能优于Sep-AMP算法.

为验证Str-EM-AMP算法的收敛性，以下对不同SNR取值情况下BER与迭代次数的关系进行仿真分析. 其中，RSN取值分别为RSN=2，4，8 dB. 仿真实验结果如图3所示.

结果表明，对于不同的RSN取值情况，所提出算法的收敛性基本稳定. 不同的RSN取值均可在较少的迭代次数(基本为7次)情况下使得算法性能趋于稳定，并基本保持不变，因此所提算法的收敛性能较好.

在仿真结果图4所示的仿真实验中，参数设置情况为：用户数U=16，单个用户射频镜面数Nt=4，调制方式4QAM，信噪比RSN=5 dB，同时设置Sep-AMP算法和Str-EM-AMP算法所迭代的最大次数Tmax=20. 观察当基站天线数Nr变化时3种算法的BER性能的变化，图中Nr从20增至80的过程中，3种算法的BER性能均逐渐变好，且Str-EM-AMP算法的BER性能最优.

4 结 论

对MBM系统中低复杂度高精度的多用户检测方法需求展开了研究，提出了一种基于AMP的多用户检测算法. 当观测矩阵满足独立同分布条件时，采用近似消息传递算法进行多用户检测可在保证高准确检测性能的同时进一步降低检测复杂度，并且所提出的算法中利用期望最大方法进行噪声方差的估计解决了在多用户检测时噪声方差未知的问题. 由所提出的Str-EM-AMP算法与MMSE算法以及Sep-AMP算法的仿真对比结果可知，所提出的Str-EM-AMP算法的BER性能更优.