网络结构下的中国银行间债务违约传染风险分析
2020-10-20刘志洋


摘要:基于KMV模型和PageRank算法,提出新的测算银行间双边风险敞口的具体方法,并从同业债务违约视角模拟分析了银行间传染风险。研究表明:在每一个年份,商业银行同业负债引发传染风险可能性的排名都不相同,呈现出时变属性;中国国有大型商业银行的传染风险权重在整个银行体系中并不突出,说明中国国有大型商业银行倒闭引发传染风险的概率很低;中小商业银行既是传染风险的主要发起者,又是主要承受者;国有大型商业银行几乎不受传染风险的影响,即使银行体系出现大规模传染危机也不会倒闭。此外,即使样本中其他23家商业银行全部倒闭,中国银行、中国工商银行、中国建设银行、中国农业银行和招商银行的资本均不会低于监管要求,说明这几家商业银行能够在传染风险中保持较高的资本充足率水平,基本不会出现倒闭风险。
关键词:商业银行;债务违约;资本充足率;网络结构;风险管理;传染风险
文献标识码:A
文章编号:1002-2848-2020(03)-0069-11
2008年金融危机证明金融创新会增加金融体系的脆弱性程度,使得金融冲击迅速传导至实体经济。这种脆弱性产生的根源在于金融创新增加了金融机构之间的关联度和金融体系的复杂性。从这个意义来讲,从网络结构视角研究系统性金融风险成为一个主要的发展趋势,学者们也将“大而不倒”(too big to fail)的思想延伸到“关联度太广而不能倒”(too connected to fail)和“处于中心化而不能倒”(too central to fail)。为了管理系统性金融风险,巴塞尔委员会在2009年提出了“系统重要性”的监管理念,并对系统重要性金融机构提出更为严格的资本充足率要求。
在确定一家金融机构的系统重要性程度时,关联度是非常重要的维度。然而,巴塞尔委员会主要依靠指标法来测算一家金融机构的系统重要性程度,并没有有效考虑金融机构之间复杂的网络结构。虽然在巴塞尔委员会发布的系统重要性指标体系中包括了关联度指标,但这些指标都来自于金融机构的资产负债表,而财务报表的信息往往没有及时更新,无法反映金融市场对商业银行资产负债信息的真实观点。金融机构之间的交易关联关系是动态的,因此金融机构的系统重要性程度也应该根据金融市场的交易情况进行动态调整,更及时地反映金融市场的观点。本文的主要贡献在于结合资本市场数据计算每家商业银行引发传染风险的可能性(即下文所称的“传染风险权重”),并使用PageRank算法估算银行间双边债务风险敞口。此双边债务风险敞口反映了市场对传染风险的判断,比单纯的最大化熵的办法更贴近实际。在此基础上,本文模拟分析银行间债务违约引发的传染风险,以期为系统性风险管理提供参考。
一、相关文献综述
2008年金融危机爆发后,测算传染风险成为系统性风险管理的一项重要工作。一家金融机构的系统重要性程度与其引发传染风险的可能性密切相关。在现实的金融体系中,系统重要性金融机构往往也是大型金融机构,因此规模往往是决定一家金融机构系统重要性程度的关键指标之一。但金融机构规模大,并不一定代表着关联度广[1]。比如,一个处在监管半径范围内的共同基金规模可能非常大,但由于其经营方式透明,且经营策略简单,因此共同基金与其他金融机构的关联度不一定非常高。但如果一家金融机构规模很小,但处在金融系统的关键节点上(比如贝尔斯登),则这家金融机构就会因为关联度广而具有很强的经营外部性,因此规模小的金融机构的系统重要性也会非常高[2]。
(一)银行间风险传染的网络结构原理
在研究传染风险方面,基于网络结构原理进行研究得到了学者的广为使用。银行网络结构原理假设商业银行通过资产业务、负债业务和表外业务等各类业务联系在一起,既通过资产负债结构,又通过金融市场紧密关联。在网络结构理论中,节点表示商业银行,有向边表示商业银行之间的业务关联。在网络结构理论中,商业银行之间的传染风险通过以下几个渠道发生:第一,违约传染渠道,其关注点主要集中于金融机构倒闭所引发的传染风险[3-4];第二,金融机构经营陷入困境引发的传染风险,其主要研究金融机构没有倒闭所引发的传染风险[5-6];第三,共同風险敞口暴露,即金融机构均暴露于同一类别的资产价格风险之下(比如2008年金融危机的房地产价格)[7-8];第四,融资渠道,即流动性风险导致金融机构相继倒闭[9-10]。
网络分析方法包括三个层面。第一个层面使用拓扑研究方法判断实体之间是否存在关联关系,对于金融机构来讲,这些关系包括交易关系、所有者关系、信贷关系等。第二个层面是对这些关联关系进行赋权。第三个层面是为节点分配自由度,来决定哪个节点能够塑造该网络结构。Battiston等[11-12]使用网络分析法计算金融机构的系统重要性程度。Thurner等[13]指出,网络分析方法能够有效地帮助金融机构挑选交易对手,继而降低交易对手信用风险。Kuzubas等[14]证明网络分析法对系统重要性程度的预测表现良好。
(二)网络分析法在传染风险研究中的使用
金融体系存在广泛的关联度。一方面,关联度越广,风险分散越充分,系统性风险越低;另一方面,关联度越广,风险扩散传染的“面”就越大。Allen等[3,15-16]较早从关联度出发,以网络视角研究金融业系统性风险。De Bandt等[15]讨论了在复杂的网络结构下,商业银行同时倒闭的传染机制:双边借贷关系受损、共同的风险敞口导致商业银行间关联度陡升、资产抛售行为导致的反馈效应以及最后的风险传染爆发。Allen等[3,16]也对金融体系的网络结构进行了理论研究。理论分析表明,金融机构之间的关联关系渠道越多,金融体系越能够有效抵御冲击[17-18]。这种分散化机制会将冲击分担至每一个金融机构,因此单个金融机构所承担的风险很小。但2008年金融危机却表明,一旦金融机构关联度过高,风险的传染性反而更强。过长的金融机构关联度链条会将一个小的冲击逐渐放大[2]。Caballero等[19-20]的实证分析表明,关联度越高,爆发金融危机的可能性越大。
对金融网络结构的关注使得学者设计反映金融体系网络结构的系统性风险测度指标。Kara等[21]将基于网络结构的测度指标分为直接指标和间接指标。直接指标关注金融机构之间的双边关联度,间接指标更加侧重使用金融市场数据研究金融机构之间的关联关系。基于网络结构的系统性風险测度方法主要包括主成分分析法、银行间敞口暴露估算以及基于跨境关联度数据的测算[22]。主成分分析法主要提取影响系统性风险的共同风险因子,Kritzman等[23-24]的研究较具代表性。而银行间敞口估算更加依靠图论进行分析[25-26]。基于跨境关联度数据的分析往往测算风险在各个国家之间的传染问题[27]。在整合学术研究基础上,International Monetary Fund等[28-29]比较了CoVaR、共同违约概率(Joint Probability of Distress,JPoD)、DY指数[30]、或有分析方法、条件违约概率等指标在测度系统性风险方面的准确性。ChanLau[25]基于关联度的思想提出应根据关联度指标来对系统重要性银行施加额外资本要求。Federal Reserve Bank of Minneapolis[31]提出,要结束“大而不倒”的观念,应根据“处于中心化而不能倒(too central to fail)”的理念来设计监管措施。
对于金融机构之间传染风险研究的难点在于缺少金融机构之间双边风险敞口的数据,尤其是金融机构之间交易的明细、高精度数据。学者们往往通过构建一个虚拟的银行体系来分析金融脆弱性。Nier等[32]分析了不同银行业结构对系统性风险的影响。Erol等[33]从银行间市场传染的角度研究如何对系统性金融风险进行监管。更多的学者使用模拟的方法解决数据缺失的问题。Gai等[34-35]开发了金融网络的传染模型,发现复杂性和集中度是导致冲击放大和脆弱性增加的主要原因。Krause等[36]考虑了多个商业银行的特征,对金融网络的刻画更加真实,认为银行间信贷是银行倒闭的主要传导机制。Elliott等[37-38]研究相互独立金融机构之间的倒闭传染问题,以及网络结构对金融体系稳定的影响。数据的缺乏也给监管当局带来了巨大的挑战,因此比利时中央银行、奥地利中央银行、英格兰银行也纷纷采用模拟的办法进行实证分析[39-41]。
中国学者对从网络结构视角研究银行间传染风险也非常关注。李宗怡等[42]模拟分析2003年底我国17家商业银行之间的传染风险,结论表明我国银行业爆发传染风险的概率很低。马君潞等[43]模拟130家商业银行的双边风险敞口,研究表明中国银行和中国建设银行具有较高的风险传染性,传染风险一旦爆发,城市商业银行会大量倒闭。随着2008年金融危机爆发,更多的学者从系统重要性视角分析商业银行引发传染风险的概率。王占浩等[44]研究表明,我国国有四大行具有一定的风险传染性,中国工商银行倒闭会引发大规模的传染风险。隋聪等[45-46]从3种网络结构和4种情景出发,对银行间债务网络进行模拟实验,研究银行间借贷比率、资本充足率等银行特征变量对传染风险的影响,发现银行间网络连接倾向具有异质性。吴念鲁等[47]研究了中国银行同业之间的流动性风险的传染问题,发现中国银行、中国工商银行、兴业银行和中国农业银行是中心节点,违约倒闭后果严重。总体而言,随着中国银行业的快速扩张以及系统重要性程度增加,传染风险较高,一旦爆发,后果严重。
从网络结构研究传染风险的前提条件是有效估计银行双边风险敞口。从交易对手信用风险来看,债权人对债务人存在风险敞口,一旦债务人违约,风险就会波及债权人。从我国银行业特征来看,存款保险制度使得99%以上的储户存款得到国家政府的保证,因此传染风险来源主要是银行间的债权债务关系。但是银行间债权债务关系的披露信息非常稀少,使得学者们需要使用一些理想的假设条件来估算每家商业银行的同业债务风险敞口,而在估算过程中所使用的数据为商业银行同业资产负债数据,主要来自于商业银行资产负债表。
研究银行间传染风险的难点在于无法公开获取银行间的双边风险敞口。虽然学者们使用了各种方法对其进行估算,但大多数学者的研究仅仅依赖于资产负债表的数据,并没有反映资本市场对传染风险的预期。随着中国大型商业银行相继上市,以及地方性城市商业银行也大批上市,运用资本市场数据研究银行间市场的传染风险,继而估算银行间双边风险敞口比单纯对敞口的分布特征进行理想化的假设更具有客观性。既然是研究银行间市场的传染风险,不可避免地需要商业银行倒闭概率的数据。本文的贡献在于基于资本市场的时间序列数据测算每家商业银行的隐含倒闭概率的时间序列以及一旦倒闭后所导致的隐含违约损失率,即在学者们对违约损失率假设的基础上,通过资本市场数据测算违约损失率,结果更具有客观性。在得到上述参数基础上,为了研究传染风险的方向性,本文将上述倒闭概率的时间序列数据纳入格兰杰因果检验的分析框架中,研究每家商业银行受其他商业银行影响的显著性水平,提取代表显著性水平的P值,作为初始矩阵代入Page等[48]提出的PageRank算法中,继而估算双边风险敞口。在此基础上,本文模拟分析商业银行在银行间市场违约后所导致的传染风险后果,以期为中国银行业系统性风险管理提供参考。
二、商业银行引发传染风险的权重测度
商业银行传染风险来自银行间双边债务风险敞口。然而,各个商业银行之间的双边债务风险敞口的精细化数据可得性较差,据笔者掌握的信息来源,没有公开可得的数据。每家上市商业银行的财务报告仅仅公开存放同业和其他金融机构存放款项以及拆入资金总额等会计科目。为了测算商业银行之间的传染风险,大多数学者均使用最大化熵假设来估计银行间的双边风险敞口。最大化熵方法假设商业银行尽可能将风险敞口平均分配至银行体系的其他商业银行。然而在实践中,由于不同商业银行在银行体系所处的地位不同,银行间市场往往呈现出“中心—四周”结构,因此商业银行并不会将风险敞口尽可能平均分配。因此,如何根据总体同业负债数据估算银行间双边风险敞口是研究传染风险的核心和难点。
双边风险敞口与传染风险大小密切相关。商业银行B对商业银行A产生传染风险的可能性越大,商业银行A对商业银行B的风险敞口就越大,即B在A的总的同业风险敞口中占比越高。因此,如果能够估计每家商业银行在银行体系中的风险传染权重,将每家商业银行的风险权重乘以某一商業银行的同业负债总额,就可以得到该家商业银行对每家商业银行的传染风险敞口。在传染风险权重测度中,权重越高,商业银行倒闭所引发的传染风险的可能性就越高。
(一)测度方法
本文使用Page等[48]提出的PageRank算法计算传染风险权重。PageRank算法需要构造邻接矩阵,A所在位置确定是行位置,B的位置确定是列位置。假设由A指向(影响)B,即如果A对B有传染风险,那么矩阵的第一行第二列是1。
PageRank算法需要得到每家商业银行的传染风险方向,但基于传统相关性的视角测度传染风险无法得到传染的方向。为了得到每家商业银行的传染风险方向,参考International Monetary Fund等[49-50]的方法,本文首先使用基于或有分析方法(contingent claim analysis)的代表性模型KMV,使用股票市场数据,测度单家商业银行隐含的倒闭概率的时间序列数据作为表示商业银行经营风险的指标[49-52],具体计算公式为
其中,ET为银行股票市值;
AT为银行资产市场价值;
DB为债务违约点;
r为无风险利率,本文使用隔夜Shibor作为代表;
N()为标准正态分布累积函数;
σA为资产市场价值的标准差;
T表示时间,本文设置为1年。假设银行资产市场价格服从对数正态分布,银行在T时间内违约概率(PD)和违约损失率(LGD)为
在测度所有样本内商业银行的违约概率时间序列基础上,本文将这些时间序列数据纳入向量自回归分析框架,并运用格兰杰因果检验方法研究每家商业银行的风险对其他商业银行风险的影响。在运用格兰杰因果检验的方法中,本文对PageRank算法中的邻接矩阵的输入进行了调整。在格兰杰因果检验中,P值的水平说明影响的显著性,因此本文使用1减去P值所得到的数值代表一家商业银行对另一家商业银行影响的显著程度,并将该值代入邻接矩阵中。在矩阵中该值越高,检验结果越显著,影响就越大。由于商业银行对自身不存在传染风险,因此本文将邻接矩阵的对角元素设置为0。在得到格兰杰因果检验P值基础上,本文通过使用PageRank算法得到每家商业银行在整个银行业中的传染风险权重,即引发传染风险可能性的大小。
(二)引发传染风险权重测度的实证结果
由于KMV模型使用的前提条件是必须有股票交易数据,因此本文的样本为中国上市商业银行。综合考虑数据可得性情况,本文的样本期间为2007年7月1日—2018年12月31日,样本商业银行包括5家国有大型商业银行(中国农业银行、中国工商银行、中国建设银行、中国银行、交通银行)、8家股份制商业银行(光大银行、华夏银行、民生银行、平安银行、浦发银行、兴业银行、招商银行、中信银行)以及15家城市商业银行(北京银行、南京银行、宁波银行、常熟银行、江阴银行、贵阳银行、杭州银行、上海银行、江苏银行、无锡银行、苏农银行、张家港银行、郑州银行、长沙银行、成都银行)。
根据KMV模型求得的每家上市商业银行倒闭风险的时间序列如图1所示。可以看出,在不同年份每家商业银行的风险走势并不完全相同,因此各年份整体银行业的传染风险特征也并不一致,所以本文在每一个年度都进行一次向量自回归分析,2007年下半年与2008年的样本数据放在一起进行向量自回归。如果在某一年份样本中的商业银行没有上市,则去掉该样本。
注:B1为中国农业银行、B2为中国工商银行、B3为中国建设银行、B4为中国银行、B5为交通银行、B6为光大银行、B7为华夏银行、B8为民生银行、B9为招商银行、B10为浦发银行、B11为兴业银行、B12为平安银行、B13为中信银行、B14为北京银行、B15为南京银行、B16为宁波银行、B17为常熟银行、B18为江阴银行、B19为贵阳银行、B20为杭州银行、B21为上海银行、B22为江苏银行、B23为无锡银行、B24为苏农银行、B25为张家港银行、B26为郑州银行、B27为长沙银行、B28为成都银行。
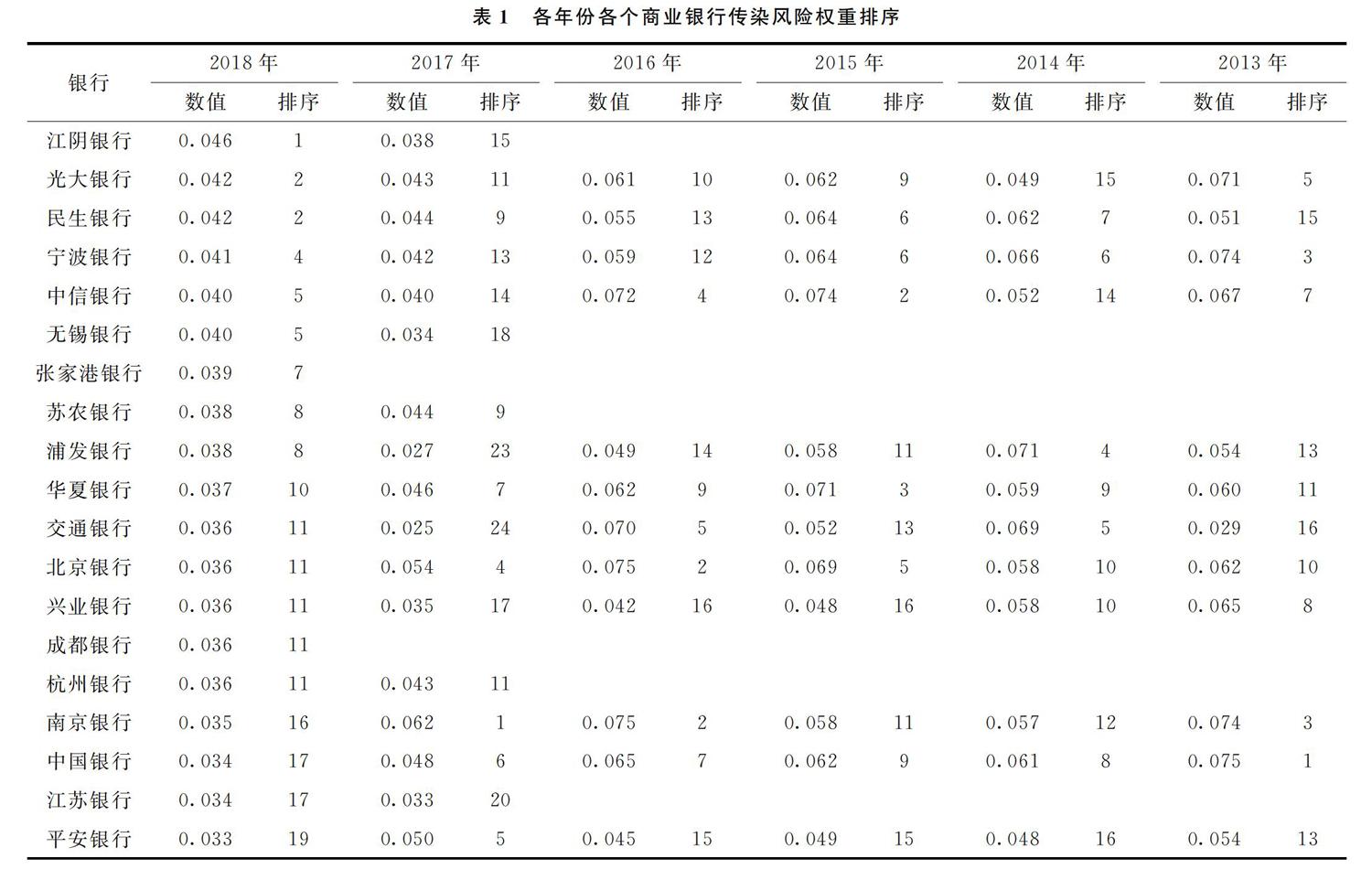
各年度各个商业银行传染风险权重排序见表1。可以看出,商业银行在各年度的传染风险权重排名并不一致,且变化较大。在全球金融危机肆虐的2007—2009年,我国国有大型商业银行的传染风险权重并不是最高。2007—2008年南京银行排名第一,且一些大型股份制商业银行的排名高于国有大型商业银行。2009年华夏银行排名第一,而2007—2008年排名第二的中国银行排名下降幅度非常大。到2010年,国有大型商业银行传染风险权重排名整体呈现了上升态势,除中国工商银行外,中国建设银行、交通银行、中国农业银行、中国银行排名均处在前列。而2011—2014年整体上国有大型商业银行的传染风险权重排名处在前列。2015—2016年国有大型商业银行传染风险权重的排名整体略有下降。2017—2018年,随着大量的中小区域性城市商业银行上市,国有大型商业银行的传染风险权重也呈现下降态势,中小商业银行的传染风险不可忽视。总体而言,我国国有大型商业银行的传染风险权重在整个银行体系中并不突出,这说明我国国有大型商业银行倒闭引发传染风险的概率很小。这一方面是因为国有大型商业银行本身倒闭的概率较小,另一方面也是因为资本市场已经预判到,一旦国有大型商业银行出现困境,国家会进行救助,因此不会引发大规模的银行业危机[53]。
三、同业债务违约传染风险模拟分析——以2018年为例
由于2018年上市商业银行个数最多,因此本文认为模拟其他年份的传染风险意义不大,因此主要模拟2018年商业银行同业债务违约导致的传染风险。
本文将银行间同业债务定义为商业银行同业和其他金融机构存放款项与拆入资金之和。在表1计算传染风险权重基础上,对于每家商业银行,本文分别对除该家商业银行之外的其他商业银行的传染风险权重进行标准化,并将重新得到的风险权重乘以商业银行的同业负债,进而求得每家商业银行对该家商业银行的双边风险敞口。根据式(4)违约损失率的测算结果,本文发现违约损失率结果都是100%,说明一旦商业银行出现债务违约,债权人会出现100%损失。假设这些损失会直接导致资本充足率的降低,一旦资本降低至零,则商业银行倒闭。此时,根据第三部分的格兰杰因果检验结果,选择倒闭的这家商业银行能够在10%水平上显著影响的商业银行并假设这些商业银行倒闭,假设这些商业银行的债权全部损失,进而引发新一轮的传染风险。如果此轮并没有导致新的商业银行传染风险,则传染终止。这时,假设按照表1中2018年的风险权重顺序,下一家没有倒闭的商业银行倒闭,引发新一轮传染风险。
2018年商业银行传染风险模拟如图2所示,箭头方向表示传染的方向。如果格兰杰因果检验显著性水平较高(即P值小于0.1),则将邻近矩阵中对应的点设置为1,否则为0。可以看出,中国商业银行体系中,中小银行受到传染风险的冲击比较大,而国有大型商业银行受到传染风险的影响比较小。此外,国有大型商业银行也并非是传染发起的主要节点,许多中小商业银行,比如宁波银行、郑州银行、江苏银行却是主要的传染风险发起点。
为了考虑监管要求,本文首先将每家商业银行风险加权资产乘以8%,得到监管资本要求。一旦债务违约导致的损失使得商业银行资本低于监管要求,监管当局就要介入,以便控制风险。本部分所有的商业银行财务数据均来自Wind数据库。
传染风险的模拟结果见表2,轮次按照表1的传染风险权重进行排序。根据2018年的传染风险权重,首先假定江阴银行率先倒闭,并开始引发传染风险。但由于江阴银行规模较小,且同业负债交易量比较小,因此江阴银行倒闭并没有导致其他商业银行倒闭,也没有导致其他商业银行资本充足率显著降低。第二轮是光大银行倒闭,光大银行倒闭直接导致常熟银行、无锡银行、苏农银行和张家港银行的倒闭,并导致成都银行、贵阳银行、郑州银行、长沙银行资本充足率低于监管要求。常熟银行、无锡银行、苏农银行和张家港银行的倒闭并没有引致其他银行的倒闭,因此本文继续模拟第三轮的传染风险,按顺序假设民生银行倒闭,这直接导致成都银行、贵阳银行、郑州银行、长沙银行等上一轮资本充足率低于监管要求的商业银行倒闭,同时导致杭州银行、南京银行、宁波银行和江苏银行资本充足率低于监管要求。随后按照顺序,宁波银行倒闭,之后中信银行倒闭引发杭州银行和南京银行倒闭,并引发华夏银行、平安银行、上海银行、北京银行的资本充足率低于监管要求。随着传染风险的逐渐加剧,单家银行倒闭所引发其他银行倒闭的个数越来越少。到第十轮,中国银行倒闭,导致招商银行资本充足率低于监管要求。模拟到第九轮发现,即使其他23家商业银行全部倒闭,中国银行、中国工商银行、中国建设银行、中国农业银行和招商银行的资本充足率均不会低于监管要求,说明这几家商业银行能够在传染风险中保持较高的资本充足率水平,基本不会出现倒闭风险。
对于中国银行业来讲,国家声誉资本的隐性注入使得政府对商业银行债务承担了隐性担保的职能。虽然2015年5月国家推出了存款保险制度,但银行间债务并不在存款保险的范畴之内。不论是区域性中小商业银行,还是全国性大型商业银行,从某种意义来讲,地方政府和中央政府均有声誉资本注入。从表2的模拟结果可以看出,一旦传染风险爆发,区域性中小商业银行会首先开始倒闭。在传染风险引发的初始阶段,大型商业银行会引发一系列中小商业银行倒闭。而这些中小商业银行都是区域性的主要商业银行,因此可以预见,当传染风险刚刚开始发生时,地方政府势必会介入,避免传染风险扩散,就像近期出现的包商银行被接管案例一样。同时从表2可以看出,我国国有大型商业银行传染风险的轮次均排在最后,且没有引发其他商业银行倒闭,这从某种意义来讲体现了政府隐性担保的力量。金融市场认为我国中央政府隐性担保将国有大型商业银行倒闭风险降至最低,且能够及时切断传染风险扩散。结合本文的模拟分析,中国银行业爆发传染风险的可能性并不大,只要政府隐性担保职能得到履行,在前两轮的传染风险中,风险应该会得到有效控制。
四、结论及政策建议
对传染风险的研究受困于数据的限制无法得到银行间双边债务风险敞口。虽然学者对同业债务风险敞口分布做了一些合理的假设,但往往距离实际较远,且过度依赖资产负债表导致测算的结果没有考虑资本市场的信息。本文基于KMV模型和PageRank算法,提出了新的测算银行间债务双边风险敞口的具体方法,并从同业债务违约视角模拟分析了银行间传染风险。整体结论表明,在每一个年份,商业银行引发传染风险可能性的排名都不相同,传染风险排名呈现出时变属性;我国国有大型商业银行的传染风险权重在整个银行体系中并不突出,说明我国国有大型商业银行倒闭引发传染风险的概率较低;中小商业银行既是传染风险的主要发起者,又是主要承受者;国有大型商业银行几乎不受传染风险的影响,即使银行体系出现大规模传染危机,也不会倒闭。
基于以上研究,本文提出如下政策建议:第一,在系统重要性评估中重视传染风险。系统重要性不应仅仅依赖规模因素,关联度导致的负外部性应该在系统重要性评估中占有重要權重。规模大的商业银行传染风险未必高,因此在系统重要性评估中应增加传染风险的权重。第二,重视中小商业银行的传染风险。中小商业银行既能够引发传染风险,又在传染风险面前表现得非常脆弱,因此增加中小商业银行抵御系统性金融风险的能力,增加中小商业银行的稳健经营程度非常重要。第三,宏观审慎监管并不能仅仅针对大型商业银行。虽然国有大型商业银行倒闭影响确实非常大,我国金融体系承受不起,但恰恰是因为市场已经预期到这一点,所以国有大型商业银行倒闭引发传染风险的概率极低。宏观审慎监管应该更加关注股份制商业银行以及中小商业银行导致的传染风险,保证这些银行具有一定的损失吸收能力,进而维护银行体系的稳定。
參考文献:
[1] Rajan R G. Too systemic to fail: Consequences, causes and potential remedies[R]. The 8th BIS Annual Conference, 2009.
[2] Yun T, Jeong D, Park S. “Too central to fail” systemic risk measure using PageRank algorithm[J]. Journal of Economic Behavior & Organization, 2019, 162(6): 251-272.
[3] Allen F, Gale D. Financial contagion[J]. Journal of Political Economy, 2000, 108(1): 1-33.
[4] Glasserman P, Young H P. How likely is contagion in financial networks?[J]. Journal of Banking & Finance, 2015, 50(1): 383-399.
[5] Tasca P, Battiston S. Market procyclicality and systemic risk[R]. ETH Risk Center Working Paper, 2012.
[6] Bardoscia M, Battiston S, Caccioli F. Pathways towards instability in financial networks[J]. Nature Communications, 2017, 8: 17.
[7] Allen F, Babus A, Carletti E. Asset commonality, debt maturity and systemic risk[J]. Journal of Financial Economics, 2012, 104(3): 519-534.
[8] Caccioli F, Shrestha M, Moore C, et al. Stability analysis of financial contagion due to overlapping portfolios[J]. Journal of Banking & Finance, 2014, 46(9): 233-245.
[9] Lee S H. Systemic liquidity shortages and interbank network structures[J]. Journal of Financial Stability, 2013, 9(1): 1-12.
[10]Acharya V V, Merrouche O. Precautionary hoarding of liquidity and interbank markets: Evidence from the subprime crisis[R]. NBER Working Paper, 2010.
[11]Battiston S, Puliga M, Kaushik R. DebtRank: Too central to fail? Financial networks, the FED and systemic risk[R]. Scientific Reports, 2012.
[12]Soramki K, Cook S. SinkRank: An algorithm for identifying systemically important banks in payment systems[J].Economics, 2013, 7(28): 1-27.
[13]Thurner S, Poledna S. DebtRanktransparency: Controlling systemic risk in financial networks[R]. Scientific Reports, 2013.
[14]Kuzubas T U, mercikolu I, Saltolu B. Network centrality measures and systemic risk: An application to the Turkish financial crisis[J]. Physica A: Statistical Mechanics and its Applications, 2014, 405(1): 203-215.
[15]De Bandt O, Hartmann P. Systemic risk: A survey[R]. European Central Bank Working Paper, No. 35, 2000.
[16]Freixas X, Rochet P J C. Systemic risk, interbank relations, and liquidity provision by the central bank[J]. Journal of Money, Credit and Banking, 2000, 32(3): 611-638.
[17]Brunnermeier M K, Pedersen L H. Market liquidity and funding liquidity[J]. Review of Financial Studies, 2009, 22(6): 2201-2238.
[18]Geanakoplos J. The leverage cycle[J]. NBER Macroeconomics Annual, 2010, 24(1): 1-66.
[19]Caballero J. Banking crises and financial integration: Insights from networks science[J]. Journal of International Financial Markets, Institutions and Money, 2015, 34(1): 127-146.
[20]Minoiu C, Kang C, Subrahmanian V S. Does financial connectedness predict crises?[R]. IMF Working Paper, No. 267, 2013.
[21]Kara G I, Tian M H, Yellen M. Taxonomy of studies on interconnectedness[R]. Board of Governors of the Federal Reserve System FEDS Notes, 2015.
[22]Bisias D, Flood M, Lo A W. A survey of systemic risk analytics[R]. Office of Financial Research Working Paper, No. 1, 2012.
[23]Kritzman M, Li Y, Page S, et al. Principal components as a measure of systemic risk[R]. MIT Sloan School Working Paper, No. 4785-10, 2010.
[24]Billio M, Getmansky M, Lo A W, et al. Econometric measures of connectedness and systemic risk in the finance and insurance sectors[J]. Journal of Financial Economics, 2012, 104(3): 535-559.
[25]ChanLau J A. Regulatory capital charges for tooconnectedtofail institutions: A practical proposal[R]. International Monetary Fund Working Paper, No. 98, 2010.
[26]International Monetary Fund. Global financial stability report: Responding to the financial crisis and measuring systemic risk[R]. World Economic and Financial Surveys, 2009.
[27]Fender I, McGuire P. Bank structure, funding risk and the transmission of shocks across countries: Concepts and measurement[R]. Bank for International Settlements Quarterly Review, 2010: 63-79.
[28]International Monetary Fund. Global financial stability report: Grappling with crisis legacies[R]. World Economic and Financial Surveys, 2011.
[29]Arregui M N, Norat M M, Pancorbo A, et al. Addressing interconnectedness: Concepts and prudential tools[R]. International Monetary Fund Working Paper, No. 199, 2013.
[30]Diebold F X, Yilmaz K. On the network topology of variance decompositions: Measuring the connectedness of financial firms[J]. Journal of Econometrics, 2014, 182(1): 119-134.
[31]Federal Reserve Bank of Minneapolis. The Minneapolis plan to end too big to fail[R]. Federal Reserve Bank of Minneapolis Working Paper, 2016.
[32]Nier E, Yang J, Yorulmazer T. Network models and financial stability[J]. Journal of Economic Dynamics and Control, 2007, 31(6): 2033-2060.
[33]Erol S, Ordoez G. Network reactions to banking regulations[J]. Journal of Monetary Economics, 2017, 89(8): 51-67.
[34]Gai P, Kapadia S. Contagion in financial networks[J]. Mathematical, Physical and Engineering Sciences, 2010, 466: 2401-2423.
[35]Gai P, Haldane A, Kapadia S. Complexity, concentration and contagion[J]. Journal of Monetary Economics, 2011, 58(5): 453-470.
[36]Krause A, Giansante S. Interbank lending and the spread of bank failures: A network model of systemic risk[J]. Journal of Economic Behavior & Organization, 2012, 83(3): 583-608.
[37]Elliott M, Golub B, Jackson M O. Financial networks and contagion[J]. American Economic Review, 2014, 104(10): 3115-3153.
[38]Acemoglu D, Ozdaglar A, TahbazSalehi A. Systemic risk and stability in financial networks[J]. American Economic Review, 2015, 105(2): 564-608.
[39]Degryse H, Nguyen G. Interbank exposure: An empirical examination of systemic risk in the Belgian banking system[R]. National Bank of Belgium Working Paper, No. 43, 2004.
[40]Boss M, Breuer T, Elsinger H, et al. Systemic risk monitor: Risk assessment and stress testing for the Austrian banking system[R]. National Bank of Austria Financial Stability Report, 2006.
[41]Alessandri P, Gai P, Kapadia S, et al. Towards a framework for quantifying systemic stability[J]. International Journal of Central Banking, 2009, 5(3): 47-81.
[42]李宗怡, 李玉海. 我国银行同业拆借市场“传染”风险的实证研究[J]. 财贸研究, 2005(6): 51-58.
[43]马君潞, 范小云, 曹元涛. 中国银行间市场双边传染的风险估测及其系统性特征分析[J]. 经济研究, 2007(1): 68-78.
[44]王占浩, 郭菊娥, 薛勇. 资产负债表关联、价格关联与银行间风险传染[J]. 管理工程学报, 2016(2): 202-209.
[45]隋聪, 于洁晶, 宗计川. 银行间债务违约诱发资产减价出售——基于债务与资产关联的风险叠加传染研究[J]. 系统工程理论与实践, 2017(11): 2753-2764.
[46]隋聪, 王宪峰, 王宗尧. 银行间网络连接倾向异质性与风险传染[J]. 国际金融研究, 2017(7): 44-53.
[47]吴念鲁, 徐丽丽, 苗海宾. 我国银行同业之间流动性风险传染研究——基于复杂网络理论分析视角[J]. 国际金融研究, 2017(7): 34-43.
[48]Page L, Brin S, Motwani R, et al. The PageRank citation ranking: Bringing order to the web[R]. Technical Report, Stanford University, 1998.
[49]International Monetary Fund. Monetary policy and financial stability[R]. IMF Staff Discussion Note, 2015.
[50]Cecchetti S G, ManciniGriffoli T, Narita M. Does prolonged monetary policy easing increase financial vulnerability?[R]. IMF Working Paper, No. 65, 2017.
[51]Anginer D, DemirgucKunt A, Huizinga H, et al. Corporate governance of banks and financial stability[J]. Journal of Financial Economics, 2018, 130(2): 327-346.
[52]Elsinger H, Lehar A, Summer M. Using market information for banking system risk assessment[J]. International Journal of Central Banking, 2006, 2(1): 137-165.
[53]陈忠阳, 刘志洋. 国有大型商业银行系统性风险贡献度真的高吗——来自中国上市商业银行股票收益率的证据[J]. 财贸经济, 2013(9): 57-66.
責任编辑、校对: 高原
The Risk Analysis of Chinese Interbank Debt Default Contagion Under Network Structure
—A Twodimensional Data Perspective of Interbank Debt and Financial Market
LIU Zhiyang
(School of Economics and Management, Northeast Normal University, Changchun 130117, China)
Abstract: Research on contagion risk is hampered by the limitations of data to obtain exposure to bilateral interbank debt. Although scholars make some reasonable assumptions about the risk exposure distribution of interbank debt, it is often far from the reality, and excessive reliance on the balance sheet will lead to calculation results without considering the information of capital market. Based on the research framework of scholars, this paper proposes a new specific method to calculate the bilateral risk exposure of banks based on the KMV model and PageRank algorithm, simulates and analyzes the risk of interbank contagion from the perspective of interbank debt default. The overall conclusion shows that for each year, the ranking of the possibility of contagion risk caused by commercial bank liabilities is different, showing timevarying property. The weight of contagion risk of large stateowned commercial banks is not very prominent in the whole banking system, which indicates that the probability of contagion risk caused by the failure of large stateowned commercial banks is very low. Small and mediumsized commercial banks are not only the initiators but also the main acceptor of contagion risk. Large stateowned commercial banks are almost immune from contagion risk and would not fail even if there were a largescale contagion crisis in the banking system. Moreover, this paper found that even if all the commercial banks, the bank of China, industrial and commercial bank of China, China construction bank, agricultural bank of China and China merchants bank were not lower than the regulatory capital requirements, this shows that these commercial banks still maintain a higher level of capital adequacy ratio in the contagion risk, basically, it will have not failure risk.
Keywords: Commercial bank; Debt default; Capital adequacy ratios; Network structure; Risk management; Risk of contagion
收稿日期:2019-12-28
基金項目:教育部人文社会科学研究青年基金项目“货币政策与宏观审慎监管协同机制及有效性检验”(19YJC790088)。
作者简介:刘志洋,男,东北师范大学经济与管理学院副教授,经济学博士,研究方向:金融风险管理与金融监管,电子邮箱:liuzy100@nenu.edu.cn。
