地震荷载下反倾层状岩质边坡倾倒变形 破坏规律及数值模拟研究

马文礼 刘赟 魏占玺 董顺德

摘 要：為了掌握不同地震荷载作用下的边坡稳定性能，采用振动台试验并结合离散元数值模拟对典型反倾层状岩质边坡进行了分析，对地震作用下反倾层状岩质边坡的动力响应特性和变形破坏规律进行了研究。结果表明：1）边坡的顶部和坡面首先出现变形，边坡开始出现层间错动导致最终彻底破坏;2）地震波频率对边坡的变形破坏有着显著影响，不同频率正弦波作用于边坡时，边坡上各个地方的加速度响应状况各不相同;3）在频率较小的正弦波作用下边坡的顶部及坡面浅表部松动变形，在频率较大的正弦波作用下边坡内部出现横向拉张裂缝，拉张裂缝会导致边坡的崩塌溃坏;4）在数值模拟分析边坡的加速度响应情况时，从边坡底部到顶部，随着高程的不断增加，其加速度放大系数增长幅度逐渐增加;5）地震波不仅影响边坡上监测点位加速度响应的大小，同时还对不同高程下其加速度响应变化情况产生影响。研究结果显示了边坡加速度响应数值模拟分析与振动台模型试验结果的一致性，所得结论对工程施工参数设计具有一定的借鉴价值。

关键词：地震学;地震荷载;反倾层状边坡;倾倒变形;加速度响应;数值分析

中图分类号：TU45;P585文献标识码：A

doi： 10.7535/hbgykj.2020yx05004

收稿日期：2020-04-04;修回日期：2020-06-28;责任编辑：张 军

第一作者简介：马文礼（1983—），男，青海门源人，工程师，主要从事工程地质与水文地质灾害防治方面的研究。

通讯作者：刘 赟工程师。E-mail： liulzylw@sina.com

马文礼，刘赟，魏占玺，等.

地震荷载下反倾层状岩质边坡倾倒变形破坏规律及数值模拟研究

[J].河北工业科技，2020，37（5）：318-325.

MA Wenli， LIU Yun， WEI Zhanxi，et al.

Numerical simulation study on deformation and failure law of overturning of anti-dip layered rock slope under seismic load[J].Hebei Journal of Industrial Science and Technology，2020，37（5）：318-325.

Numerical simulation study on deformation and failure law of

overturning of anti-dip layered rock slope under seismic load

MA Wenli1，2，3， LIU Yun1，2，3， WEI Zhanxi1，2，3， DONG Shunde1，2，3

（1.Qinghai Bureau of Environmental Geology Exploration，Xining，Qinghai 810001， China; 2.Qinghai Engineering Research Center of Geo-environment Protection and Disaster Prevention， Xining，Qinghai 810001， China; 3.Key Laboratory of Environmental Geology of Qinghai Province， Xining，Qinghai 810001， China ）

Abstract：

In order to explore the slope stability under different seismic loads， the typical anti-dip layered rock slope was analyzed by shaking table test and discrete element numerical simulation， and the dynamic response characteristics and deformation and failure laws of anti-dip layered rock slope under earthquake were studied. The results show that：1） the top and surface of the slope deform at first， and the interlayer dislocation of the slope begins to appear， which leads to complete failure; 2） the seismic wave frequency has a significant influence on the deformation and failure of the slope， and when sine waves with different frequencies act on the slope， the acceleration response varies from place to place; 3） the loosening and deformation appear on the top and shallow part of the slope under the action of the sine wave with lower frequency， and the transverse tensile cracks appear inside the slope under the action of the sine wave with higher frequency， and the further development of the tension crack finally leads to the collapse of the slope; 4） in the process of numerical simulation analysis of the acceleration response of the slope， the growth rate of acceleration amplification coefficient increases gradually with the increase of elevation from the slope bottom to the top; 5） seismic wave not only affects the acceleration response of each point on the slope， but also affects the change of acceleration response at different elevations. The study shows that the numerical simulation analysis of slope acceleration response is consistent with the shaking table model test results， which has a certain practical significance for the design of construction parameters and the early design and construction of similar projects in the future.

Keywords：seismology; seismic load; anti-dip layered slope; toppling deformation; acceleration response; numerical analysis

地震是一种常见的自然灾害，其发生时往往还伴随着泥石流[1]、滑坡[2]等次生灾害[3]。随着中国基础建设的高速发展，在西部山区修筑公路和隧道等基础工程的建设项目逐渐增多，地震荷载下的边坡稳定性问题也随之显现[4-5]。

目前，中国针对地震作用下的边坡稳定性能分析还处于初步探索阶段。学者们从不同角度分析了地震荷载作用下的边坡稳定性能[6-8]。刘新荣等[9]研究了高频微小地震对于三峡库区边坡的影响，探索了顺层状岩质边坡收到微小地震的响应状况;宋丹青等[10]基于拟静力法、模型试验方法、能力分析方法等研究了岩质边坡的地震动力稳定性，为以后的相关研究提供了理论基础;罗洋等[11]通过ABAQUS软件建模的方法模拟分析了微小地震下边坡动力响应规律;段彦福等[12]应用动力响应时程分析法研究了地震加速度下边坡加固之后的动力响应。这些研究通过模型试验、具体案例分析等方式研究了不同地震荷载作用下顺层状岩质边坡、加筋土双边坡的具体响应。在已有研究中尚未发现针对反倾层状岩质边坡的地震荷载作用下边坡倾倒变形破坏规律的研究。

地震荷载下边坡的动力响应对于判断边坡的稳定性有着很重要的作用，通过振动台模拟试验可以分析边坡的加速度响应特征。为了能够更好地分析地震荷载下反倾层状岩质边坡的变形和破坏特征，本文通过建立边坡模型，探讨地震作用下边坡的响应规律，并对在相同频率正弦波作用下边坡不同监测点位的加速度响应特征进行数值模拟分析。通过对比边坡模型和数值模拟分析的结果，验证边坡振动台试验的准确性和实际应用的可行性。

1 振动台模型试验设计

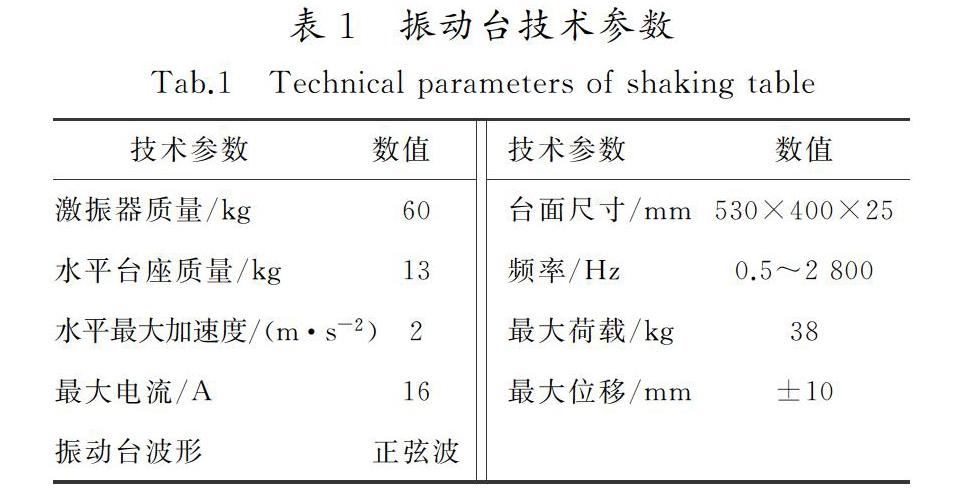
振动台试验使用的模拟振动台系统是由北京波谱世纪科技发展有限公司开发研制的WS-Z30-50小型精密模拟振动台系统。其产品技术参数如表1所示。

1.1 试验相似律

1.1.1 相似关系

综合考虑试验目的、设备技术参数、模型特性等因素，选取长度、弹性模量、密度作为主控因素，并且采用基本物理量量纲，取模型长度相似常数为60，弹性模量相似常数为3，密度相似常数为100，依照推导的相似指标，求出其余物理量的相似常数。试验各物理量的相似常数如表2所示。

1.1.2 相似材料

以石膏作为相似材料，设计制作了1∶60的反倾层状岩质边坡模型。经过大量室内力学试验研究，确定试验最终配比为水膏体积比为1∶0.8，其物理力学参数如表3所示。

1.2 模型箱设计与测点布置

试验中边坡模型是由单独的模块堆砌而成，模块尺寸为12 cm×6 cm×2 cm。具体的边坡模型设计尺寸如图1 a）所示。

边坡模型的制作过程可以分为3个阶段：

1）按配比配置石膏浆液，浇筑在预先安置好隔离钢板的模型箱中，制成与模型箱接触良好的板材，放入烘干箱中以75°恒温烘干;

2）将板材摆放在卧放的模型箱中，首先，用记号笔按照设计好的尺寸进行标记，尽量保证板材的分割线错位排列，确保在堆砌的过程中不出现横向贯通的结构面，然后，取出标记好的板材进行切割，制作成试验设计的模块，并对模块按照摆放顺序进行编号，确保堆砌工作顺利进行;

3）按比例配置黏结剂，依据各模块编号进行堆砌，制作完成的边坡模型需在自然条件下放置一段时间等待黏结剂干燥。堆砌过程中依据涂刷遍数控制模块与模块之间的黏结强度，确保边坡模型与模型箱边界接触牢固，在振动过程中不产生相对位移。制作完成的边坡模型如图2所示。

试验中共采用了12个加速度传感器，其中有7个（ZT1—ZT7）属于振动台自带传感器，另外5个（DC1—DC5）为附加的加速度传感器。各个加速度传感器在模型上的布置情况如图1 b）所示。从图1 b）边坡模型的监测分布可以看出：模型上的ZT2，ZT7，DC1，DC3这4种传感器在边坡模型的坡面上均匀分布;ZT3，ZT5，DC2，DC4这4种传感器均匀分布在边坡模型内部;ZT4，ZT5，ZT6，ZT7这4种传感器分布于边坡模型的同一高度平面上。

1.3 试验加载制度

为了分析振动试验过程中边坡模型的动力特性，在试验加载过程中多次对边坡模型施加噪声激励。由于与边坡模型自振频率相近的正弦波具有比地震波更强的破坏力，可以在振动台允许的加载范围内持续增加振动强度，直至边坡模型破坏，因此，试验选择正弦波作为震源，选择加载5，15，25 Hz 3种频率的正弦波，振动时间保持10 s。

正弦波用正弦波信号发生器（sine wave generator）自动生成[13-15]。图3为振幅0.1g、持续时间10 s、频率5 Hz的正弦波加速度时程曲线。试验过程中通过改变正弦波的频率来研究边坡的振动响应特征。

2 地震作用下的边坡响应规律

试验主要分析在不同频率正弦波振动荷载下，在坡面、坡内竖向、水平位置上的加速度传感器响应。

2.1 正弦波作用下边坡加速度响应峰值变化规律

1）5 Hz正弦波作用

在5 Hz正弦波作用下边坡加速度响应图如图4所示。

从图4中可以发现：在5 Hz正弦波的作用下，边坡模型的坡面、坡内和同一水平高度上的加速度响应峰值都呈现逐渐增加的趋势。当振幅超过0.2g时，随着振幅的增加，边坡模型下部监测点的加速度响应增长速度慢慢变缓。当振幅小于0.2g时，边坡上各个监测点的加速度响应峰值變化趋势一致。从图4 c）中可以看出当监测点处于同一高度时，随着振幅的逐渐增加，其各个监测点的加速度响应峰值保持一致。说明在相同高度下，边坡模型上监测点的加速度响应峰值随正弦波（5 Hz）振动强度的变化规律保持基本一致。

通过设计边坡的模型试验，探讨了地震作用下反倾层状岩质边坡变形的破坏机理，并结合数值模拟软件分析了边坡不同高程下的加速度响应情况，得出以下结论。

1）反倾层状岩质边坡在地震的荷载下首先出现变形的位置是边坡的顶部和坡面。随着振动和振幅的增加，坡体出现滑坡现象，滑坡的出现进一步加剧了边坡顶部和坡面的破坏。随着边坡开始出现层间错动导致最终的边坡彻底破坏。

2）地震波的频率对于反倾层状岩质边坡的动力响应有很大的影响。不同频率正弦波作用于边坡时，其不同地方的加速度响应状况各不相同。当频率为15 Hz的地震波施加于边坡时，其动力响应表现出很明显的高程放大效应;当模拟地震的正弦波频率小于或者大于15 Hz时，反倾层状岩质边坡上各部位的加速度放大系数下降。地震波的频率不仅能够影响边坡的加速度响应规律，还能影响边坡上加速度响应大小分布的范围。

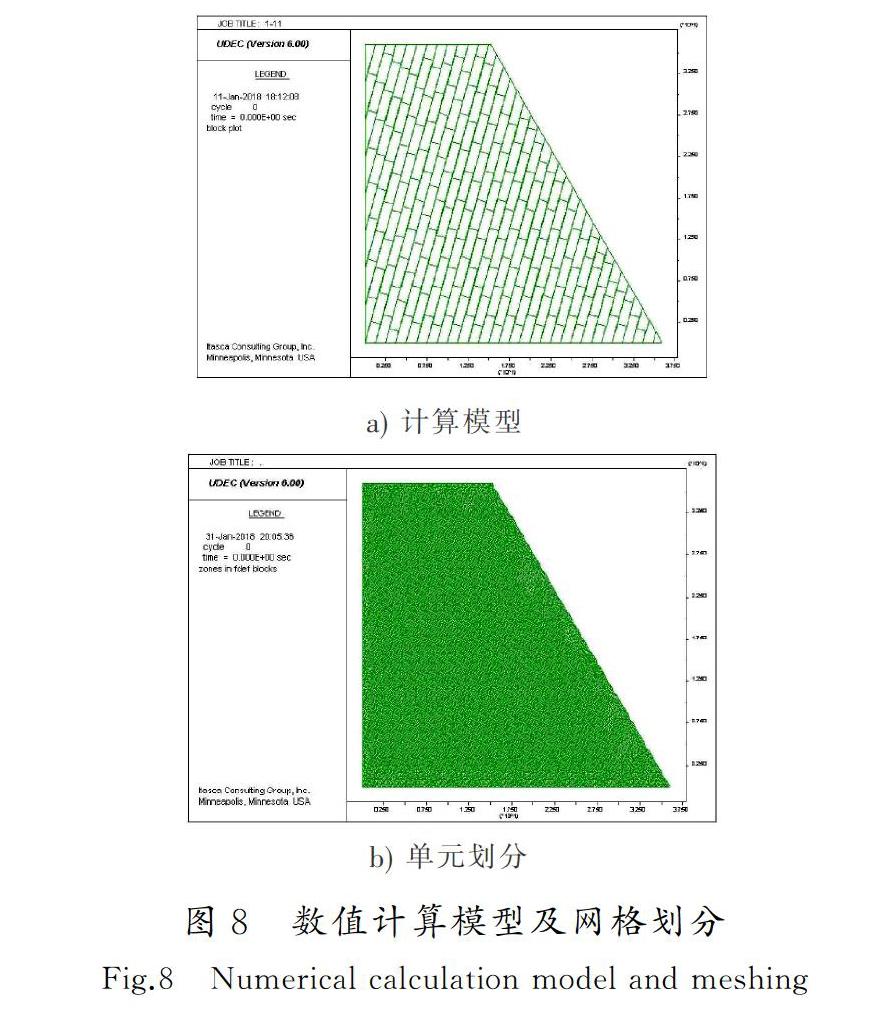
3）在数值模拟分析边坡的加速度响应情况时，当正弦波为15 Hz时，随着边坡距离地面的高程逐渐增加，坡面和坡内的加速度放大系数也逐渐增加，当高程较小时，其加速度放大系数增加的更明显。从边坡底部到顶部，随着高程的不断增加，其加速度放大系数增长幅度逐渐增加。

4）边坡加速度响应数值模拟与振动台模型试验中的加速度放大系数变化情况一致，说明数值模拟分析能够很好地反映振动台模型试验结果，试验结果具有良好的指导作用。

由于边坡动力响应问题复杂、振动台模型试验工作量大、以及试验条件的限制，本研究还有一些问题有待深入研究：1）试验在层状边坡的模拟并不能完全模拟反倾层状边坡的真实结构，今后应加强数值模拟在岩层接触关系方面的研究;2）在水平向振动研究的基础上，研究边坡在竖向地震力作用下的动力响应特性和变形破坏规律。

参考文献/References：

[1] 赵高文，王萌，杨宗佶，等.震后泥石流沟内滑坡堰塞坝的侵蚀特征分析——以银洞子堰塞坝为例[J].工程科学与技术，2019，51（5）：68-77.

ZHAO Gaowen，WANG Meng， YANG Zongji， et al. Eroding characteristics of landslide dams in debris flow gullies after earthquakes—Case study of Yindongzi landslide dam[J]. Advanced Engineering Sciences， 2019，51（5）：68-77.

[2] 任祥，汪班桥，李楠.地震作用下锚固滑坡的动力响应特性研究[J].西安建筑科技大学学报（自然科学版），2019，51（5）：676-681.

REN Xiang， WANG Banqiao， LI Nan. Study on dynamic response of anchorage landslide under earthquake at different loading magnitude[J]. Journal of Xi′an University of Architecture and Technology（Natural Science Edition） ，2019， 51（5）： 676-681.

[3] 刘亢，孙柏涛，李亦纲，等.2015年尼泊尔Ms8.1地震震害分布与地质构造关系研究[J].自然灾害学报，2019，28（5）：59-65.

LIU Kang， SUN Baitao， LI Yigang， et al. Study on the relationship between the earthquake damage distribution and geological structure of the 2015 Ms8.1 Nepal earthquake[J]. Journal of Natural Disasters，2019，28（5）：59-65.

[4] 牛涌，楊兴振，赵建林，等.基于上限分析法的含夹层边坡地震稳定性分析[J].公路交通科技，2019，36（1）：38-45.

NIU Yong， YANG Xingzhen， ZHAO Jianlin， et al. Analysis on seismic stability of slope containing interlayer based on upper bound analysis method[J]. Journal of Highway and Transportation Research and Development，2019，36（1）：38-45.

[5] 代仲海，胡再强，尹小涛，等.工程荷载作用下缓倾角反倾似层状岩质边坡变形稳定性分析[J].岩土力学，2018，39（sup1）：412-418.

DAI Zhonghai， HU Zaiqiang， YIN Xiaotao， et al. Deformation stability analysis of gently inclined layer-like rock slope under engineering load[J]. Rock and Soil Mechanics， 2018，39（sup1）：412-418.

[6] 李结全. 地震作用下裂缝高切坡稳定性极限上限分析[J].工程勘察，2019，47（2）：21-25.

LI Jiequan. Seismic stability analysis on high cutting slope with cracks by using upper bound limit analysis[J]. Geotechnical Investigation and Surveying，2019，47（2）：21-25.

[7] NAKATA N， SNIEDER R， KURODA S， et al. Monitoring a building using deconvolution interferometry. I： Earthquake-data analysis[J]. Bulletin of the Seismological Society of America， 2013，103（3）：1662-1678.

[8] WANG Jiading， XU Yuanjun， MA Yan， et al. Study on the deformation and failure modes of filling slope in loess filing engineering： A case study at a loess mountain airport[J]. Landslides，2018，15（12）：2423-2435.

[9] 刘新荣，许彬，刘永权，等.频发微小地震下顺层岩质边坡累积损伤及稳定性分析[J].岩土工程学报，2020，45（4）：632-641.

LIU Xinrong， XU Bin， LIU Yongquan， et al. Cumulative damage and stability analysis of bedding rock slope under frequent microseisms[J]. Chinese Journal of Geotechnical Engineering，2020，45（4）：632-641.

[10]宋丹青，陳志荣，陈俊栋.岩质边坡地震动力响应研究进展[J].水利与建筑工程学报，2018，16（6）：1-7.

SONG Danqing， CHEN Zhirong， CHEN Jundong. Advances in the seismic dynamic response rock slope[J]. Journal of Water Resources and Architectural Engineering，2018，16（6）：1-7.

[11]罗洋，姚添智.不同震动参数对反复微小地震下边坡动力响应规律的影响[J].四川建筑科学研究，2019，45（6）：55-59.

LUO Yang，YAO Tianzhi. Effect of different ground motion parameters on dynamic response of slopes under repeated micro-seismic action[J]. Sichuan Building Science，2019，45（6）：55-59.

[12]段彦福，宋玲，刘杰，等.地震作用下土工格栅加筋土双边坡动力分析[J].科学技术与工程，2019，19（32）：300-306.

DUAN Yanfu， SONG Ling， LIU Jie， et al. Dynamic analysis of geogrid reinforced soil double under seismic action[J]. Science Technology and Engineering，2019，19（32）：300-306.

[13]王英浩，刘鹏程.拟合地震波作用下综合管廊抗震有限元分析[J].应用力学学报，2020，1（14）：1-8.

WANG Yinghao， LIU Pengcheng. Seismic finite element analysis of utility tunnel under fitting seismic wave[J]. Chinese Journal of Applied Mechanics， 2020，1（14）：1-8.

[14]公伟增，段宝福，张雪伟，等.隧道爆破地震波作用下砌体建筑物振动响应分析[J].科学技术与工程，2019，19（33）：377-383.

GONG Weizeng， DUAN Baofu， ZHANG Xuewei， et al. Analysis of vibration response of surface masonry buildings under tunnel blasting seismic wave[J]. Science Technology and Engineering，2019，19（33）：377-383.

[15]李康，王威，杨典森，等.周期振荡法在低渗透测量中的应用研究[J].岩土力学，2020，1（3）：1-9.

LI Kang， WANG Wei， YANG Diansen， et al. Application of periodic oscillation method in low permeability measurement [J].Rock and Soil Mechanics，2020，1（3）：1-9.