基于供需平衡的社会型长期护理保险缴费水平研究

张宁 王佳 李旷奇

摘 要：在界定老年人失能状态的基础上，将多状态马尔可夫模型与ILO筹资模型相结合，构建了一个供需平衡下的社会型长期护理保险缴费模型。同时，对50岁及以上各年龄段人群的健康状态转移概率矩阵进行估计，结合人口数据估算和预测未来处于不同失能状态的人口数量;并对长沙市未来缴费人口和社会平均工资水平进行预测，估算了未来长沙市社会型长期护理保险缴费水平。

关键词： 社会型长期护理保险;缴费水平;多状态马尔可夫模型

中圖分类号：F840.612   文献标识码： A    文章编号：1003-7217（2020）05-0028-08

一、引 言

随着人口老龄化发展，伴随机能老化、慢性病而来的失能老人数量增长和失能时间不断延长等现象层出不穷，与失能人口密切相关的长期护理问题也日益严峻。尽管早在2005年就有保险公司推出商业型长护险，但由于投保年龄受限且费用过于昂贵，十余年来商业型长护险未能获得广大民众的青睐。为了应对失能老人对个人和家庭的财务冲击，2016年6月，人社部出台《关于开展长期护理保险制度试点的指导意见》，在全国15个地区开展长期护理保险试点工作，开启了国家层面推行社会型长护险的序幕。不过，由于各个试点地区间尚未形成统一的长护险缴费水平确定标准，这既可能导致个人或财政负担加重，也不利于长期护理保险制度在全国范围推行。由此可见，研究社会型长期护理保险缴费水平，确立一套便于实施的缴费水平确定方法，能够为长护险在全国范围内的推广奠定基础，具备迫切的现实意义。

已有研究长期护理保险缴费水平的文献，根据其研究对象的不同，可以分为两类：一是对商业型长期护理保险缴费水平进行研究，二是对社会型长期护理保险缴费水平进行研究。

1.商业型长期护理保险缴费水平确定方法主要有曼联方法、减量表方法和多状态Markov模型。曼联方法通过大样本抽样调查得到失能者的年平均护理时间，以此推算失能者所需的护理费用，再进行费率厘定。Meiners M R等（1984）基于曼联模型计算了不同年龄段下的人群在不同假设条件下的费率[2]。减量表方法通过观察个体在多个减量表的转移情况获取转移概率，从而确定缴费水平。Haberman S（1984）认为减量表方法可以通过分析不同健康状态的人数变化情况来估算状态转移概率[3]。陈岱婉（2008）在减量表模型基础上建立了考虑到生存和死亡给付责任的综合责任长期护理保险的精算模型，该模型考虑到了生存和死亡的给付责任[4]。多状态Markov模型是在确定转移概率的基础上测算长期护理保险费。Helms F等（2005）使用广义最小二乘法估计了多状态Markov模型参数，在假定的转移概率下计算出长期护理保险的费率[5]。Lally N R等（2016）认为Tweedie分布的广义线性模型能更好地预测长期护理保险的费率[6]。王新军和王佳宇（2018）对我国老年人的健康状态转移概率影响因素进行测算，在此基础上用Markov模型对长期护理保险的费率进行了计算[7]。

2.社会型长期护理保险的定价方法多采用基于现收现付制的定价方法和基于积累制的定价方法。基于现收现付制的定价方法是构建一个长期护理保险基金，保证基金在存续期间每年支出与收入相等，以此确定缴费水平。陈璐和徐南南（2013）参照德国、日本的长护险模式，测算出1995-2010年我国的长期护理保险缴费水平处于0.07%～0.26%[8]。林珊珊（2013）构建长期护理保险基金收入和支出模型，认为应该把长期护理保险城镇职工缴费率约定为1%左右[9]。曹信邦和陈强（2014）测算出我国2015-2050年的长期护理保险总体费率水平，认为我国实施长期护理保险的初始成本较低，但费用负担越来越重[10]。基于积累制的定价方法是为每个参保人构建一个长期护理保险积累账户，计算出参保人员在未来可能的长期护理费用支出的现值，以此确定参保人员的缴费水平。胡晓宁等（2016）研究表明，初始状态为健康时，女性费率高于男性;而初始状态为失能时，男性与女性的费率有不同的变动趋势[11]。荆涛等（2016）提出了将社会型和商业型长期护理保险结合的政策性长期护理保险概念，测算出了18～60岁人口参保的缴费水平[12]。

但从现有文献来看，对社会型长期护理保险缴费水平的研究大多基于不同年龄段人口的失能比例在未来不发生变化这一假设，即未来失能人数的预测仅是将人口预测数量和现有失能比例的简单相乘，并未考虑失能的动态转化情况。但是现实生活中，老年人各失能状态是互相转移的，即老年人的失能状态是不断发生变化的。此外，关于护理方式的选择大多数借鉴的是国外数据，与我国实际情况相比会有所出入。这些都可能降低长护险缴费水平测算的精准性。

为此，首次将基于多状态Markov模型得到的健康状态转移概率矩阵与ILO筹资模型相结合，在重点考虑人口的健康状态转移变化规律的基础上，构建失能老人长期护理保险供需平衡精算模型，以此确定缴费水平，放松了失能转移概率不变这一不合现实的假设，以使测算结果更为精确;同时，构建多状态Markov模型对失能状态按相关规定进行细分，并且考虑更低年龄段人口，然后基于CHARLS数据得到我国50岁及以上人口的五状态转移概率矩阵，以弥补现有关于我国人口在各状态下的转移规律研究的不足。

二、数据及描述性统计

（一）数据来源

使用的数据主要有：一是中国健康与养老追踪调查数据（CHARLS），基于此数据估算50岁及以上人口的健康状态转移概率以及失能比例数据;二是长沙市统计年鉴、中国统计年鉴和中国人身保险业经验生命表（2010-2013），基于此数据可以估算长沙市未来不同年龄段人数;三是已有文献中长沙市机构护理的成本费用数据和长沙市人口对不同护理方式选择比例的数据。

按上述過程估算2018-2032年长沙市50岁及以上的不同健康状态城镇人口数（见表6）。

2.护理方式选择比例。对护理方式的选择比例选取谢凡（2018）[20]的关于长沙市居民护理方式选择的问卷调查数据，将长沙市城镇居民选择居家社区护理方式的比例定为84.12%，选择机构护理方式的比例定位15.88%。

3.不同护理方式成本。对不同护理等级老人选取不同护理方式的成本使用谭睿和卢婷（2015）对长沙市养老机构为不同护理等级老年人提供护理服务费用的实地调查数据[21]，可以得到2014年长沙市不同护理方式和护理等级的护理费用（见表7）。

假设护理费用增长率与GDP增长率保持一致，2017年之前的GDP增长率用实际数据，2017年及以后的GDP增长率选用李标等（2018）[22]对GDP增长率的预期，即2017-2020年的增长率为6.6%，2021-2015年的增长率为6.02%，2020-2030年的增长率为5.52%，2031-2035年的增长率为5.05%;并且同时考虑到CPI因素的影响，将CPI值设为2014-2018年的均值1.80%，从而可以得到未来每年不同护理等级及护理方式下的费用 （见表8）。

4.测算的结果。综合之前建立的模型以及变量的选择，估算出长沙市2017-2032年长期护理保险基金的总需求（见表9）。

（三）长期护理保险基金总收入

1.缴费人数。对社会型长期护理保险缴费人群年龄的确定参考国内试点情况，即包括所有参与职工医保的人群，同时考虑到60岁及以上人群退休这一情况，未将60岁及以上人群纳入长期护理保险缴费人群，从而界定20～59岁的城镇居民为长期护理保险的缴费人群。

根据2017年中国统计年鉴和2017年长沙市统计年鉴可以估算出长沙市2017年分年龄段的人口数据，然后结合中国人身保险业经验生命表（2010-2013）可以估算出长沙市未来各年龄段的人数，进而得到长沙市未来社会型长期护理保险的缴费人数（见表10）。由于老龄化的发展，未来人口结构会发生变动，用现有的生命表来预测未来的人口数具有相对的准确性，这也是未来研究可以进一步深入之处。

2.年平均工资。根据长沙市统计年鉴数据可以得到长沙市居民2017年人均可支配收入为41131元。假设其增长率与实际GDP增长率保持同步，同时考虑CPI因素的影响，设CPI为2014-2018年的均值1.80%，可以得到长沙市居民未来年平均工资水平（见表11）。

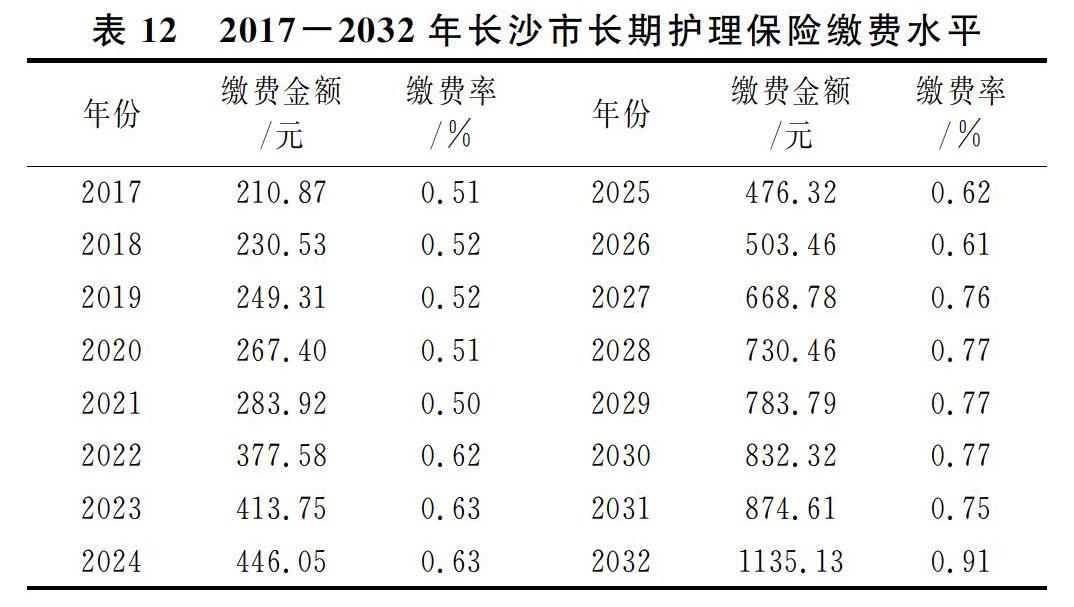
3.测算的结果。依据ILO筹资模型，长期护理保险基金的总需求支出与长期护理保险基金的总供给收入相等，由2017-2032年的长期护理保险基金总需求结合估算的长沙市长期护理保险缴费人数和平均工资水平，可以求出2017-2032年长沙市长期护理保险缴费水平（见表12）。

五、结论与建议

以上研究显示：（1）基于求得的健康状态转移概率矩阵，发现我国50岁及以上的人群健康状态转移规律有以下特点：随着年龄的增加，初始状态为健康的人群在一年后保持原状态的概率下降，状态恶化的概率上升;初始状态为轻度失能的人群在一年后保持原状态的概率下降，状态好转的概率下降，状态恶化的概率上升;初始状态为中度失能的人群在一年后保持原状态的概率先下降后上升，状态好转的概率先上升后下降，状态恶化的概率上升;初始状态为重度失能的人群在一年后保持原状态的概率上升，状态恶化的概率上升，状态好转的概率下降。（2）根据模型及测算结果，长沙市社会型长期护理保险在2017年的财务总需求为7.86亿元，缴费率为0.51%，缴费金额为210.87元;在2032年的财务总需求为36.94亿元，缴费率为0.91%，缴费金额为1135.13元;在15年间，长沙市社会型长期护理保险的财务总需求增长5倍，缴费率增长近1倍，缴费金额增长5倍。可以看出，相较于我国现行的8%的城镇职工基本养老保险个人缴费率水平和2%的城镇职工医疗保险个人缴费率水平，社会型长期护理保险的缴费率水平较低，适合我国实际情况，个人、政府以及企业对其具有足够的财务负担能力，但也应注意到社会型长期护理保险缴费水平增长速度较快。

鉴于长沙市社会型长期护理保险缴费率的测算结果，实现财务供需平衡的缴费水平和缴费率在未来会出现大幅上涨，因此，长沙市社会型长期护理保险缴费水平的确定应考虑到财务供需平衡;同时，在这一基础上针对未来大幅上涨的缴费水平积极采取应对措施，如拓宽筹资渠道、缴费水平的确定尽量立足于中长期水平，从而减少因为缴费率的大幅变动带来的不利影响。

注释：

① 包括吃饭、控制大小便、上厕所、穿衣服、洗澡、上下床。

② 包括慢走1公里，在椅子上坐时间久了再站起来，连续不停地爬几层楼，弯腰、屈膝或者下蹲，提10斤重的东西，做家务活，做饭，去商店买食品杂货，管钱，吃药。

参考文献：

[1] 荆涛，谢远涛.我国长期护理保险制度运行模式的微观分析[J].保险研究，2014（5）：60-66.

[2] Meiners M R， Trapnell G R.Long-term care insurance： premium estimates for prototype policies [J]. Medical Care， 1984， 22（10）：901-91.

[3] Haberman S.Decrement tables and the measurement of morbidity： I [J]. Journal of the Institute of Actuaries ， 1983， 110（2）：361-381.

[4] 陈岱婉. 综合责任长期护理保险的精算模型[J]. 山西师范大学学报（自然科学版）， 2008， 22（1）：40-43.

[5] Helms F， Czado C， Gschll S.Calculation of LTC premiums based on direct estimates of transition probabilities[J].Astin Bulletin the Journal of the Internationl Actuarial Association，2005，35（2） ：455-469.

[6] Lally N R，Hartman B M.Predictive modeling in long-term care insurance[J]. North American Actuarial Journal，2016，20（2）：160-183.

[7] 王新军，王佳宇.基于Markov模型的长期护理保险定价[J].保险研究，2018（10）：87-99.

[8] 陈璐，徐南南.中国长期护理保障制度的财政负担——基于德、日社会保险模式的测算[J].保险研究，2013（1）：106-118.

[9] 林姗姗.我国长期照护保险制度的构建与财务平衡分析[J].福建师范大学学报（哲学社会科学版），2013（1）：28-34.

[10] 曹信邦，陈强.中国长期护理保险费率测算[J].社会保障研究，2014，20（2）：111-122.

[11] 胡晓宁，陈秉正，祝伟.基于家庭微观数据的长期护理保险定价[J].保险研究，2016（4）：57-67.

[12] 荆涛，杨舒，谢桃方.政策性长期护理保险定价研究——以北京市为例[J].保险研究，2016（9）：74-88.

[13] 中国老龄科学研究中心课题组.全国城乡失能老年人状况研究[J].残疾人研究，2011（2）：11-16.

[14] 黄枫，吴纯杰.基于转移概率模型的老年人长期护理需求预测分析[J].经济研究，2012，47（S2）：119-130.

[15] 崔晓东.中国老年人口长期护理需求预测——基于多状态分段常数Markov分析[J].中国人口科学，2017（6）：82-93，128.

[16] 胡宏伟，李延宇，张澜.中国老年长期护理服务需求评估与预测[J].中国人口科学，2015（3）：79-89，127.

[17] 何文炯，洪蕾.中国老年人失能状态转移规律研究[J].社会保障研究，2013（6）：45-55.

[18] Israel R B ， Rosenthal J S ，Wei J Z.Finding generators for markov chains via empirical transition matrices，with applications to credit ratings[J].Mathematical Finance，2010， 11（2）： 245-265.

[19] 何燕华.健康老龄化战略下我国长期照护制度的反思与重构[J].湖湘论坛，2018 （5）：95-107.

[20] 谢凡.长沙市长期护理保险发展模式研究[D].长沙：湖南大学，2018.

[21] 谭睿，卢婷.长沙市老年长期护理费用测算及保障制度研究[J].保險职业学院学报，2015，29（5）：27-31.

[22] 李标，齐子豪，丁任重.改革进程中的中国潜在GDP增长率：估计及预测[J].当代经济科学，2018，40（6）：1-13，126.

（责任编辑：宁晓青）