基于RGB-D相机的多视角机械零件三维重建
2020-10-20信寄遥陈成军李东年
信寄遥 陈成军 李东年


摘 要:为了低成本且高效的实现对机械零件的三维重建和参数测量,研究了利用RGB-D相机从6个角度拍摄机械零件,获得零件不同角度的深度图像与彩色图像,通过坐标转换将深度图像转换成点云数据。首先利用滤波算法去除点云噪声,分割出机械零部件的点云数据,并利用PCA主成分分析法计算点云数据的法向量;使用最近点迭代算法(ICP)实现相邻三视角点云数据的配准,得到正背面的点云,将正背面点云进行旋转融合得到最终的目标点云数据;最后使用泊松重建算法得到完整闭合的零件三维模型。实验结果表明本文的三维重建方法具有较好的鲁棒性和准确性,重建得到的三维模型细节清晰,点云误差较小。
关键词:三维重建;点云配准;模型重构;最近点迭代算法;Kinect
中图分类号:TP391.4 文献识别码:A
3D Reconstruction of Mechanical Parts Using Multi-view RGB-D Images
XIN Ji-yao,CHEN Cheng-jun?,LI Dong-nian
(School of Mechanical & Automotive Engineering,Qingdao University of Technology,Qingdao,Shandong 266520,china)
Abstract:In order to realize the 3D reconstruction and measurement of surface parameters of mechanical parts with low cost and high efficiency,the mechanical parts are taken from 6 angles by RGB-D camera,and the depth and color images of different angles of mechanical part are obtained,and the depth image is converted to point cloud data by coordinate transformation. firstly,the filtering algorithm is used to remove the point cloud noise,and segment the point cloud data of the mechanical components. And Principal Component Analysis (PCA) is ued to calculate the normal vector of the point cloud data. Secondly,by the Iterative Closest Points(ICP)method,the registration of the adjacent three-point point cloud data is realized. So the point cloud on the back side,is rotated and fused to obtain the final target point cloud data. Finally,the Poisson reconstruction algorithm is used to obtain the 3D model. The experimental results show that the proposed 3D reconstruction method has better robustness and accuracy,and the reconstructed 3D model has clear details and less point cloud error.
Key words:3D reconstruction;point cloud registration;model reconstruction;iterative closest points;kinect
三維重建技术是指通过计算机数字化手段,建立客观世界中的三维实体数学模型的过程,在虚拟现实、计算机视觉等领域具有很多的应用。三维重建技术通过计算机对采集到的物体点云数据进行数字化建模,将物体的三维信息存储到计算机中,通过获取的物体三维信息可以对物体进行精准测量和建模,为进行逆向工程或者三维建模提供数据支持[1]。利用激光扫描仪获得目标物体的数据进行三维重建在古建筑、文物保护、工业零件测量等领域具有广阔的应用前景[2-6]。但是现今的激光扫描仪或者TOF相机在价格上非常昂贵,对于工业上单一零件的测量成本过高,所以低成本且精确的三维扫描技术就有了应用的空间。
在三维重建方面,Nieβner[7]等实现了基于高效的存储数据结构的大规模且精细的实时三维重建系统,提高了三维重建技术在大规模环境中应用的性能与质量;Izadi[8]等实现了实时的三维重建系统Kinect Fusion,但是该方法不能适应快速移动的应用场景,且会产生较大的噪声;Fan[9]等改进了现有的深度神经网络生成三维数据的方法,提出了一个条件形状采样器,能够从输入图像预测多个合理的三维点云;Tatarchenko[10]等改进了编码器-解码器网络构建三维结构的方法,建立了两种分别执行图像分类和检索的替代方法,实现了较好的结果。
选用的三维重建示例为减速器箱体的上壳体,箱体类零件一般是指具有一个以上孔系,内部有一定型腔或空腔,在长宽高方向上有一定比例的零件。箱体类零件在机械、汽车、航空航天等行业受到了广泛应 用,例如汽车的发动机缸体、汽车减速器的箱体;各类机床的主轴箱等。箱体类零件将机器或部件中的轴、套、齿轮等有关零件组成一个整体,使他们之间保持正确的相互位置,并且按照一定的传动关系协调的传递运动或者动力。因此,箱体的加工质量会直接影响整个机器或部件的精度、性能和寿命。
提出了一种低成本、高精度的机械零部件三维重建数字化方法。首先固定住RGB-D相机使其不能移动,按照一定角度(60°)旋转箱体零件,通过RGB-D相机采集到的箱体零件在六个视角下的彩色和深度图像,对采集到的图像进行预处理得到六个视角下的点云数据,然后通过两次配准和融合点云数据得到完整的零件点云。此外,对基于该三维重建方法得到的箱体点云进行泊松重建处理,得到箱体零件的三维模型。
1 基于RGB-D相机的重建流程
实现多视角机械零部件三维重建主要在于将多个视角分别配准为正面与背面点云然后进行二次配准,整体算法的流程图如图1所示。
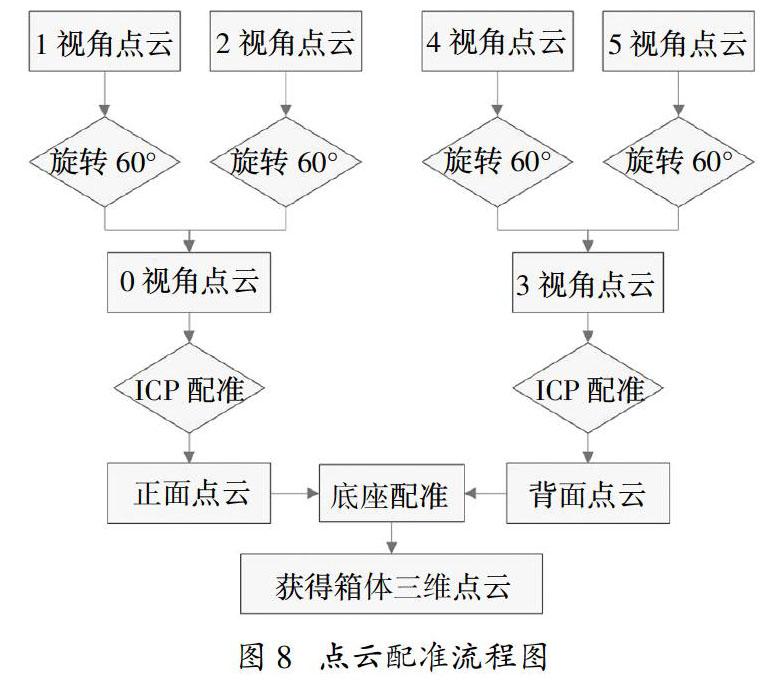
利用RGB-D相机进行三维重建时,首先要获取机械零部件每个视角的深度图像与彩色图像,然后转换得到六个视角的三维点云数据;分别对三个视角的点云进行ICP配准得到正面以及背面点云,计算中心点进行旋转融合得到零件点云;最后用泊松重建算法得到零件的三维模型。
1.1 实验设备与信息采集
使用的RGB-D设备为Microsoft Kinect V2 3D体感摄像机,以齿轮减速器箱体为实验对象,研究机械零部件的多视图三维重建。
如图2、3所示,使用Kinect V2摄像机对减速器箱体进行拍摄,距离约为70 cm,从6个角度对减速器箱体的点云数据采集完成后,按确定的顺序手动旋转放置减速器箱体的底座约60°,对减速器箱体的下一个角度进行采集,直到完成6个角度的点云数据采集。每个视角分别获取5帧的深度图像(424像素*512像素)与彩色图像(1080像素*1920像素),处理得到点云数据
1.2 点云数据的获取
1.2.1 采集范围的设置
在利用Kinect传感器采集点云数据之前利用PCL增加条件设置(add Comparison)过滤掉非条件设定范围的点云,防止环境点云产生过多的干扰。Kinect传感器拍摄视角的坐标轴如图4所示。对于Z值范围设置为:0.001 m 1.2.2 深度图像转换为三维点云 如图4所示,深度图像转换为三维点云的过程就是图像点m(u,v)映射到世界坐标系点M(xw,yw,zw)的过程,转换公式表达如下: 其中u、v为图像坐标系下的任意坐标点。u0、v0分别为图像中的中心坐标。xw,yw,zw表示世界坐标系下的三维坐标点。zc表示相机坐标的Z轴值,即目标到相机的距离。R、T分别为外参矩阵的3*3旋转矩阵和3*1平移矩阵。 由于世界坐标原点和相机原点是重合的,即不需要旋转和平移,因此 由于相机坐标系和世界坐标系原点重合,因此相机坐标与世界坐标下的同一物体具有相同的深度,即zc = zw,所以由以上变换矩阵可以得到图像点 [u,v]T到世界坐标点[xw,yw,zw]T的变换公式为: 由于Kinect传感器自身噪声和跳动的问题,导致同一视角采集到的深度图像数据有不同程度的变化。在1 s内拍摄5帧彩色与深度图像进行融合,可以有效地消除Kinect自身的噪声和跳动问题,并且可以优化点云数据的处理效果。本文处理融合后的深度图像得到的点云数据每幅约39000个点。 1.3 滤波处理及法向量计算 1.3.1 地面点云的去除 Kinect传感器在采集点云数据的时候会将设定范围内的地面连同减速器箱体及底座全部采集并生成点云,而在后续进行点云配准和融合的时候地面点云将会干扰法相计算以及配准,所以需要将地面点云提前去除掉。选用一种简单有效地方法去除地面点云,即假设Kinect为水平放置,如图5所示。先采集一张未放置减速器箱体及底座的点云,该点云即为地面点云。通过遍历点云中点的三维信息,处理得到地面点云中的Y值(即纵轴)最大值YMax1,即Y值小于YMax1的点即可判定为地面点云中的点,大于YMax1的点可以判定为减速器箱体及底座点云中的点。使用该种方法能够快速有效的去除地面点云。 1.3.2 处理底座与地面的点云 将底座放置在设定的目标区域内,采集得到底座和地面同时存在的点云,如图6所示,同上对地面点云的处理一样,假定Kinect传感器为水平放置,通过遍历该点云中每個点的三维信息,处理得到该点云中所有点Y值的最大值YMax2。由此可得,Y值小于YMax2且大于YMax1的点为底座的点云,Y值大于YMax2的点为减速器箱体的点云。在后续对多个视角的点云进行配准时会使用到YMax2的值。 1.3.3 离群点过滤 通过Kinect传感器的测量误差,获得的点云数据集会产生稀疏的离群点,估计局部点云特征的运算很复杂,这些离群点会产生错误的数值,在后面进行搞得点云配准,本文采用条件滤波法:对每一个点的邻域进行一个统计分析,并修剪掉那些不符合一定标准的点。该方法基于在输入数据中对点到临近点的距离分布的计算,对每个点计算它到它的所有临近点的平均距离。假设得到的结果是一个高斯分布,其形状由均值和标准差决定,平均距离在标准范围(由全局距离平均值和方差定义)之外的点,可被定义为离群点并可以从数据集中去除掉。 [2] 張瑞菊,王晏民,李德仁. 快速处理大数据量三维激光扫描数据的技术研究[J]. 测绘科学,2006,31(5):93-94. [3] 金涛,陈建良,童水光. 逆向工程技术研究进展[J]. 中国机械工程,2002(16):1430-1436. [4] 徐胜勇,卢昆,潘礼礼,等. 基于RGB-D相机的油菜分枝三维重构与角果识别定位[J]. 农业机械学报,2019,50(02):28-34. [5] 翟瑞芳,张剑清. 基于激光扫描仪的点云模型的自动拼接[J]. 地理空间信息,2004,2(6):37-39 [6] 曾月鹏. 基于三维图像的逆向工程重构系统[J]. 现代电子技术,2018,41(20):176-179. [7] NIEBNER M,ZOLLHOFER M,IZADI S,et al. Real-time 3D reconstruction at scale using voxel hashing[J]. ACM Transactions on Graphics,2013,32(6):1-11. [8] IZADI S,KIM D,HILLIGES O,et al. Kinect fusion:real-time 3D reconstruction and interaction using a moving depth camera[C]//Proceedings of the 24th annual ACM symposium on User interface software and technology. ACM,2011:559-568. [9] FAN H,SU H,GUIBAS L J. A point set generation network for 3d object reconstruction from a single image[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017:605-613. [10] TATARCHENKO M,RICHTER S R,RANFTL R,et al. What do single-view 3D reconstruction networks learn[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019:3405-3414. [11] BESL P J,MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,1992,14(2):239-256. [12] BLAIS G,LEVINE,M.D. Registering multiview range data to create 3D computer objects[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(8):820-824. [13] KAZHDAN M,BOLITHO M,HOPPE H. Poisson surface reconstruction[C]//Proceedings of the fourth Eurographics symposium on Geometry processing,2006.
