基于谐波分解的余干地震台接收函数研究
2020-10-20查小惠曾文敬郭雨帆
查小惠,赵 影,曾文敬,罗 丽,郭雨帆
(江西省地震局,南昌 330026)
关键字:接收函数;谐波分解;各向异性
0 引言
接收函数方法[1]研究地壳结构已被广泛应用。随着观测资料的增多,研究方法的深入,基于不同方位角接收函数的变化研究台站下方地壳不均匀性的论文越来越多[2-5]。目前在研究横向不均匀性中研究最多的是界面倾斜和各向异性,而各向异性中又以HTI(水平对称轴的横向各向同性)介质为主。在众多使用接收函数研究地壳不均匀性的方法中,谐波分解[6]是一种较为常用的方法。谐波分解方法的主要原理是根据倾斜界面和各向异性导致的Pms震相随方位角时间变化周期存在差别[7-8]。界面倾斜导致Pms震相随方位角呈2π周期变化,HTI介质中Pms震相随方位角呈π周期变化,谐波分解方法可以在Pms震相的相对时差中分离出这两种叠加在一起的时间变化,从而分析台站下方的横向不均匀性。本文首先基于水平对称轴各向异性介质接收函数Pms到时理论公式和理论地层模型,分析并验证谐波分解方法的可行性和可靠性。然后将该方法应用到江西余干地震台(图1),基于江西省地震局台网中心多年来积累的连续波形资料,进一步验证谐波分解方法在实际台站中的应用效果,探讨余干台站下方的地壳不均匀性。
1 方法及理论测试
1.1 方法原理
根据前人研究[7-8]显示,单层水平对称轴各向异性介质接收函数Pms到时可以近似表达为

其中,t0为各向同性介质Pms震相到时,δt是各向异性介质所引起的时差,θ为接收函数的后方位角,φ是各向异性快波方向。根据接收函数不同后方位角Pms震相的到时变化,可以基于谐波分解的方法,反演得到公式(1)中的模型参数,理解台站下方的介质结构参数。
本文首先使用理论公式和理论模型得到一系列的理论Pms震相到时,然后利用harmfit函数对该到时进行谐波拟合,通过理论试验,验证分析程序的可靠性,同时理解各反演参数间的对应关系。最后将该方法应用到实际台站当中,获取实际台站下方可靠的地壳结构参数。
1.2 理论接收函数测试
1.2.1基于公式的理论测试
基于公式(1),假设t0=5,δt=0.3,φ=45°。反方位角从0°到360°,以10°为间隔,总共37道,计算出Pms震相的走时(图2)。然后对计算出的Pms震相走时使用harmfit函数进行谐波分析,验证谐波分解程序的可靠性。研究发现,使用harmfit进行谐波分析时,需要去除Pms震相走时的直流分量,否则拟合不准确。去除掉直流分量后,使用harmfit进行4阶谐波分析,得到结果参数为表1,拟合图形为图2,图2中实线为公式计算的理论Pms震相去直流后的走时,虚线为使用harmfit函数拟合得到的Pms震相走时。
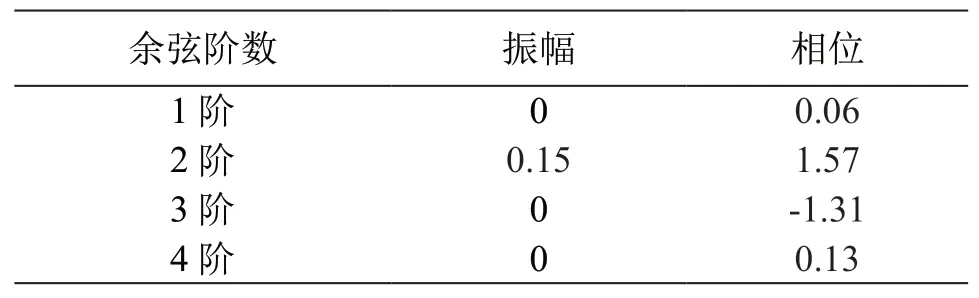
表1 harmfit函数4阶谐波分析结果Table 1 The fourth order harmonic analysis results of harmfit function
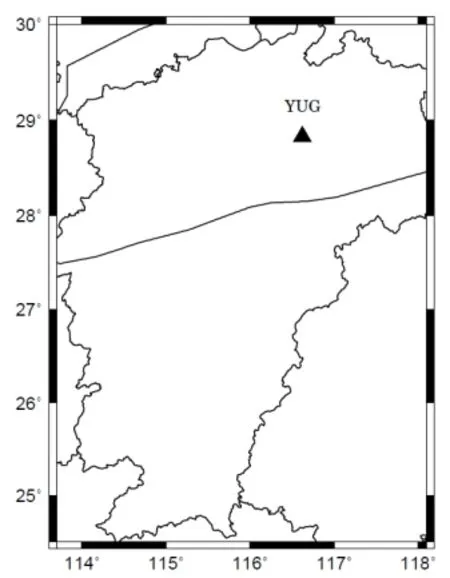
图1 YUG地震台位置图Fig.1 Location map of YUG station

图2 理论和谐波拟合的Pms震相走时图Fig.2 Pms phase travel time diagram fitted with harmonics
根据表1可以看到,1,3,4阶的振幅都为零,根据harmfit函数说明,得到的二阶谐波表达式应该为AMP*cos(2t+ALP),其中AMP为振幅,ALP为相位,单位是弧度。二阶的振幅为0.15,振幅的2倍为0.3,和假设的δt=0.3一致。相位信息为1.57,为弧度结果,接近pi/2,二阶表达式可以写成0.15*cos(2*t+1.57),根据cos函数的公式cos(θ-pi)=-cos(θ)。可以将二阶表达式写成-0.15*cos[2(θ-pi/4)],和(1)式对照认为,harmfit谐波分解结果和假设的参数是一致的。通过该理论公式和harmfit的函数拟合,验证了harmfit函数谐波分解的正确性,并知道如何理解harmfit的谐波分解参数。
1.2.2 基于模型的理论测试
为了更深入的理解各向异性地壳模型产生的接收函数Pms震相走时变化,谐波分解方法对地壳各向异性的分析能力,本文设定了两个地壳模型(表2)。使用谐波分解方法分析理论地层模型的Pms震相走时数据,验证了程序的可用性并更深入的理解了相关参数的对应关系。

表2 计算接收函数的地层模型Table 2 Strata models used for receiver function modeling
对A1和A2两个地层模型,使用RAYSUM程序[9]合成理论的RTZ三分量地震记录,射线参数设为0.05 s/km,高斯脉冲宽度设为0.5 s,采样间隔设为0.01 s,总共5024个采样点,360°的反向方位角以10°为间隔观测,总共37道接收。再将理论合成的RTZ三分量地震记录利用迭代反褶积[10-11]得到R分量的接收函数,接收函数高斯低通滤波参数设为3,大约对应1 Hz的拐角频率。求取得到理论接收函数以后使用脚本将反方位角、射线参数等信息写入接收函数头文件,方便后续处理。

图3 A1模型Ps震相Fig.3 Ps phase of A1 model

图4 A1模型Ps震相对齐时差曲线Fig.4 Ps phase alignment time difference curve of A1 model
根据Ps震相的到时,选取接收函数时间窗3.5 s~6 s进行分析(图3)。以反方位角为0°的接收函数为参考道,其它道接收函数向该道接收函数对齐,计算出每道相对第一道的时间偏移量,可以看出各道接收函数的时间偏移连线显示明显的余弦曲线特征(图4)。需要说明的是,时间偏移曲线的余弦特征和参考道的选取没有关系,选取任何一个反方位角的接收函数作为参考道,得到的时间偏移曲线余弦特征不变,但是相对到时在数值上存在一个常量的整体的平移。利用harmfit函数对相对时差进行谐波分析,可以得到不同阶余弦函数的振幅和相位(表3),下面我们对谐波分解结果进行分析。

表3 模型A1和A2谐波分解结果Table 3 Harmonic decomposition results of model A1 and A2
Raysum软件中各向异性的定义是基于百分比,假设各向异性强度K可以写为其中Vmax为快波速度,Vmin为慢波速度;快慢波走时差dt可以表达为其中L为各向异性层厚度。将(1)式代入(2)式可得(3)式L*K=dt*Vmin(3)。在A1和A2模型中L为20 km,模型中给出的是平均速度为3.5 km/s,各向异性强度K为5%时,计算可得Vmin约为3.41 km/s,可以算出理论的时间延迟应该为0.29 s左右。
根据harmfit函数说明,得到的2阶谐波表达式应该为AMP*cos(2t+ALP),ALP为弧度,可以认为使用harmfit求解两个理论模型的时间延迟分别为0.30 s和0.28 s,和理论时间0.29 s的时间延迟相符,快轴方向分别约为-6°和39°,和理论的0°和45°相近但有误差。基于理论模型的计算,我们认为该方法可以较好的提取单层水平对称轴各向异性地壳模型的地壳结构信息,后续将在实际资料处理中,进一步验证。
2 实际台站处理
基于前文理论公式和理论模型的谐波分解结果可以知道,只要精确获取不同方位角的Ps震相相对时间偏差,通过谐波分解,可以得到各向异性的快波方向和时间延迟。但在实际处理过程中,接收函数存在噪声,且接收函数方位角覆盖不完整,这些都会影响到不同方位角相对时差的提取,进而影响谐波分解的可靠性。本文基于江西余干地震台,细致分析了方位角覆盖的完整性问题,基于波形互相关方法提取Pms的相对时差。然后利用谐波分解方法对台站接收函数进行了分析,对结果进行了解释。
2.1 方位角完整性分析
为了分析地震事件方位角覆盖情况,本次以余干地震台为中心,挑选出2011年到2019年5.5级以上地震,震中距在30°到95°之间记录的远震总共1837个。以10为间隔,将反方位角分为36个区间,统计每个区间接收函数的数量(表4)。同时绘制地震震中分布图(图5)。根据表4和图5可以明显看出,地震事件的方位角分布是非常不均匀的。反方位角从50°到110°只有5个地震事件,地震事件为个位数的反方位角区间也还有9个,如果这些地震事件求取的接收函数形态不好,会导致这些方位角的接收函数约束缺失,这对我们使用不同方位角接收函数反演地壳结构是非常不利的。对于某些方位角,如120°~130°,地震事件数量达到665条,存在很大的冗余。虽然地震事件分布很不均匀,但地壳横向不均匀性造成的Pms震相周期较大,根据采样定理,当前的方位角覆盖完全可以对对信号进行恢复。
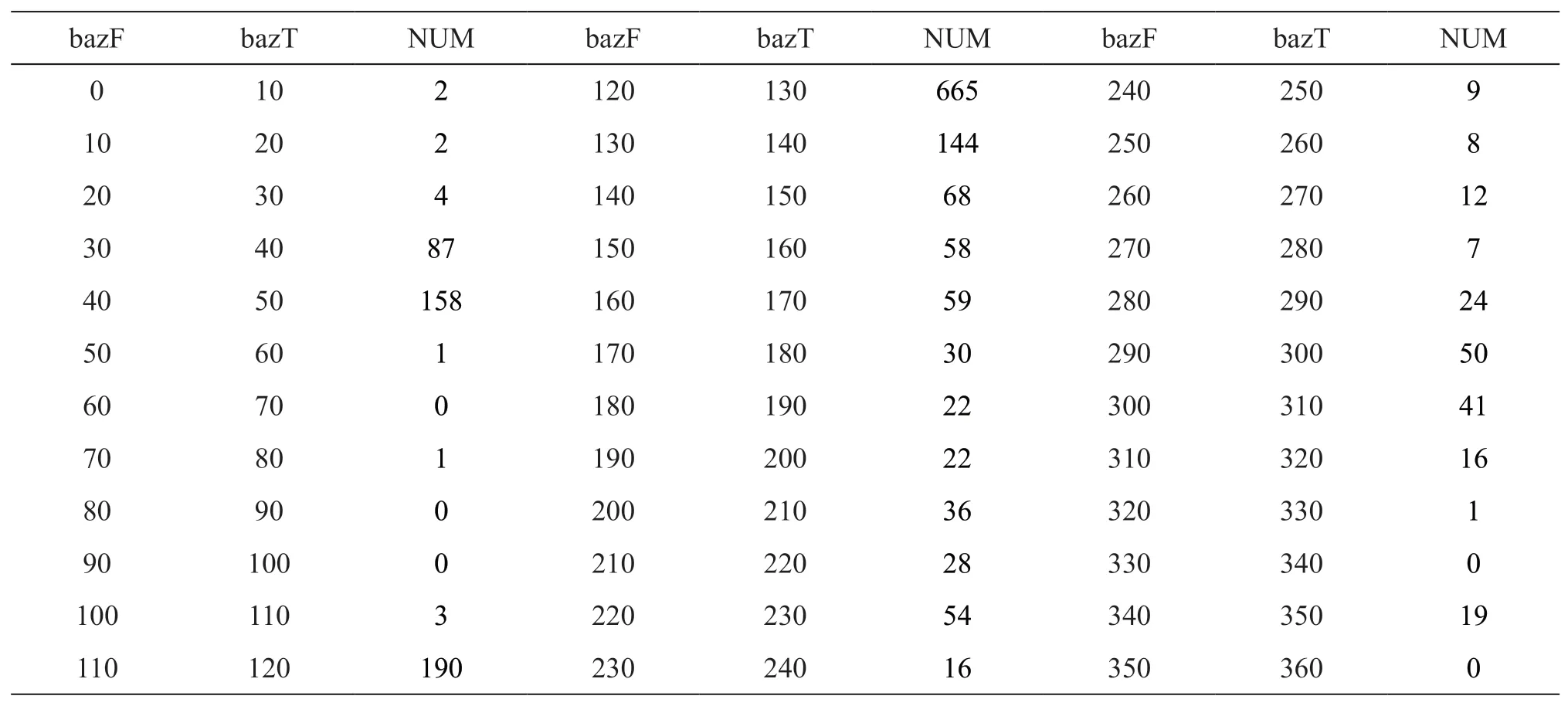
表4 YUG台2011—2019不同方位角接收函数数量Table 4 Number of receiver functions in different azimuths of YUG station from 2011 to 2019
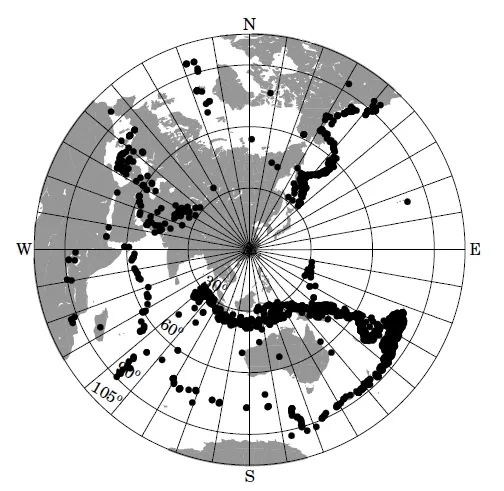
图5 2011—2019年远震震中分布图Fig.5 Epicenter distribution of teleseismic from 2011 to 2019
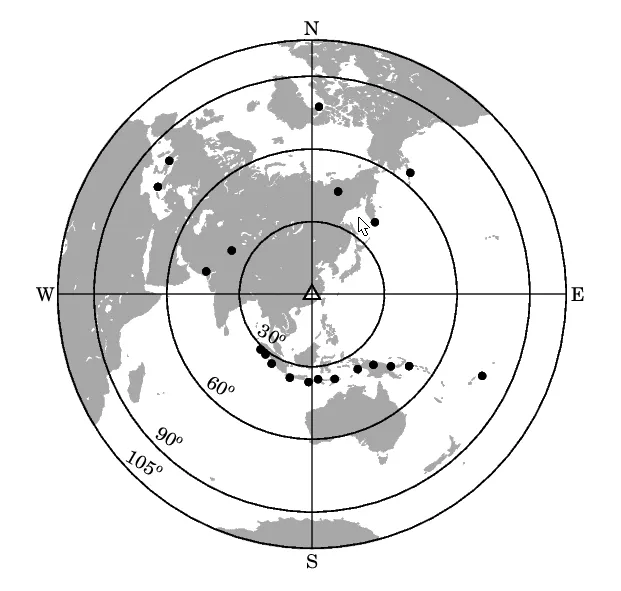
图6 使用的地震事件震中分布图Fig.6 Epicenter distribution map of earthquakes used
在实际处理过程中,基于地震事件震中方位角分布的不均匀性,本文采取如下接收函数挑选方法。首先基于接收函数的形态,在所有接收函数中挑选出Ps震相较为清晰,波形质量较好的接收函数,然后对于某一个方位角范围,在挑选好的多个接收函数中挑选出一条高质量的可代表该方位角接收函数特征的事件参与不同方位角的接收函数反演。而对于接收函数很少的方位角区间,逐条挑选,确保方位角的覆盖能达到最大。
2.2 实际台站处理
本次使用的地震资料时间跨度较长,使用了2007—2017年的地震资料。选择震中距在30°~95°之间的5.5级以上远震,截取P波初至前20 s和初至后80 s事件波形进行接收函数计算,带通滤波频率为0.1~2.0 Hz,迭代次数设置为100、接收函数的高斯低通滤波系数设为3.0(该系数对应的拐角频率约为1 Hz)。挑选到267条接收函数,然后每个方位角选择1条接收函数参与反方位角计算,总共有20条接收函数参与计算,参与计算的地震震中分布图见图6。
首先对20条接收函数进行动校正,校正到震中距为67°的标准。然后按反方位角排列,突出显示2.3 s~4.3 s的波形,可以明显看到Pms震相存在到时差(图7)。

图7 余干台Ps震相Fig.7 Ps phase of YUG station
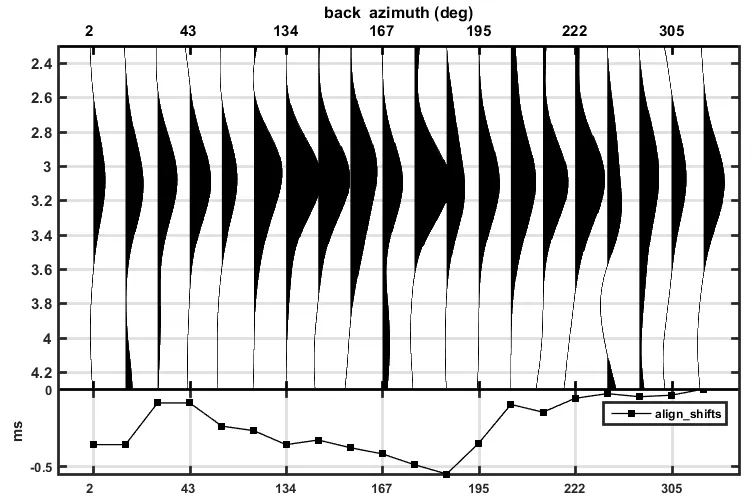
图8 余干台Ps震相对齐时差曲线Fig.8 Ps phase alignment time difference curve of YUG station
利用波形互相关方法将余干台20道接收函数Ps震相对齐(图8),得到不同方位角的Ps震相相对走时差,然后进行谐波分解,4阶谐波分解结果见表5。基于表5的二阶谐波分析结果,可以认为地壳各向异性的时间延迟约为0.28 s,快波方向为83°。但是谐波分解结果显示,1阶和4阶的振幅系数也较大,这表明台站下方的结构较为复杂,仅仅使用水平轴的各向异性地层模型很难解释,可能要考虑倾斜界面甚至其它更复杂的地壳结构模型才可以完全解释不同方位角的Ps震相时间偏差。
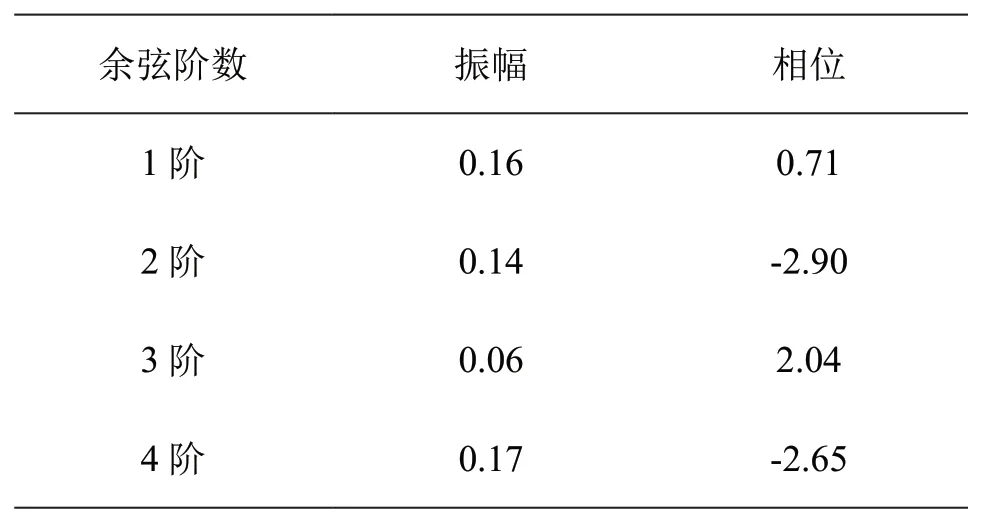
表5 余干台4阶谐波分解结果Table 5 The fourth order harmonic decomposition results of Yugan station
3 结论和讨论
本文基于各向异性介质下Pms震相到时的理论公式和理论地层模型,验证了谐波分解方法求取地壳各向异性参数的可行性和可靠性。对江西余干地震台实际资料处理,认为余干台地壳各向异性的快波方向约为83°,时间延迟约为0.28 s。在处理中发现,Pms相对到时的拾取精度对谐波分解结果的影响是很大的。本文通过波形互相关方法对齐Pms震相,求取相对时差,发现并不是每个反方位角Pms震相的波峰都可以对齐。因为波形互相关计算的是给定时间区间内波形的整体相似度。韩明等[5]提出可以通过提取不同方位角Pms震相波峰最大值的时间,然后进行谐波分解,本文进行了尝试,但结果相差不大。余干台接收函数谐波分解的结果显示,2阶谐波并不能完全拟合Pms震相的相对时差,表明台站下方还存在倾斜等其它横向不均匀性。王琼等[12]研究认为倾斜界面的存在不会对快波方向产生影响,但是会影响延迟时间的计算的。所以本文得到快波方向参数比延迟时间具有更高的准确性。
杨晓瑜[13]使用SKS分裂方法研究了长江中下游地区地幔的各向异性,结论为快波方向总体呈现E-W向,平均快波方向为86.19°,和本文得到的余干台地壳各向异性快波方向较为一致,支持华南地区壳幔耦合变形的观点。石玉燕等[14]对华东地区部分台站进行了SKS分裂研究,包括余干地震台。文中的得到的余干地震台快波方向为102°,时间延迟为0.9 s。快波方向和本文的结果存在一定的差别,需进一步分析。本文得到的时间延迟小于0.3 s,结合前人得到的SKS时间延迟,支持地幔的各向异性强于地壳的观点。与前人结果的对比进一步证明了本文方法和结论的可靠性,未来将该方法进一步用于江西地区的其它台站研究,为理解该区的形变机制提供更多的约束。
致谢:本文使用的谐波分解基础函数为harmfit,来 自GITHUB,num-matlab-master软 件包,作者为François Beauducel
