注意力机制与改进RNN的混合音乐推荐算法研究

杨明极，刘 畅，宋 泽

1(哈尔滨理工大学 测控技术与通信工程学院，哈尔滨 150080) 2(中国船舶重工集团公司第七〇三研究所 蒸汽事业动力部，哈尔滨 150010)

1 引 言

伴随互联网技术的迅速普及，各类信息的数据呈现爆发式地增长.预计到2025年，全球数据总量将是2018年的5.3倍，高达到175ZB[1]，即产生信息爆炸.面对如此庞大的信息总量，如何快速、准确地为用户提供最感兴趣的内容就成为一个非常有意义的研究课题.为此，诸多推荐技术应运而生[2]，数字音乐领域中的个性化音乐推荐已然成为各类线上音乐服务中的必备服务，例如Spotify、QQ音乐、网易云音乐等都嵌入了各自的推荐算法，极大地增强了用户对该产品的依赖程度，同时缩短了用户找到喜爱音乐的时间.

传统的音乐推荐算法随着可感知数据的不断增多，无法充分利用用户和音乐之间的深层次特征，导致推荐质量下降.使用深度学习的方法可以从每一层中自动抽取特征，从而提升分类的精度[3].深度神经网络(Deep Neural Network，DNN)的出现，解决了音乐数据难以处理的问题[4]，但DNN以向量为输入，并且不能捕捉音频数据在时间序列上的关系，而这种关系对于音乐推荐十分重要.循环神经网络(Recurrent Neural Network，RNN)理论上可以对任意长度的序列数据进行建模，并对过去的信息进行记录.由于音频的上下文是相关联的，并且这种联系直接影响到音乐推荐的准确度.因此，RNN更适合应用于音乐推荐领域.

Okura等人使用RNN从用户的历史行为列表中学习用户偏好[5].Liu等人采用RNN建模用户行为并提出一种循环Log双线模型，实现对用户下一时刻的行为类型预测[6].Van等人通过将用户历史收听数据和音频信号组合卷积神经网络，将用户和音乐映射到一个隐空间，得到用户和歌曲的隐表示，从而较好解决音乐推荐系统中的冷启动问题[7].尽管上述研究已经取得一定的成果，但由于RNN在序列上共享参数，会产生梯度消失或梯度爆炸的问题[8].而长短时记忆网络(Long Short-term Memory，LSTM)模型可以较好的解决该问题[9].Jia等人提出一种基于特征分割的LSTM模型，推荐的精确度比基于RNN模型提高4%[10].但由于音乐领域音频特征序列较长，LSTM无法捕捉较长的序列，同时存在着梯度衰减的问题.独立循环神经网络(Independent Recurrent Neural Network，IndRNN)可以通过调整反向传播梯度和使用Relu非饱和激活函数解决梯度消失问题，并且增强模型的鲁棒性，比LSTM更适合分析长时序特征[11].同时IndRNN将RNN层内的神经元进行解耦，使每个神经元之间相互独立，增加可解释性.但由于音频信号特征较多且时间尺度较长，使用IndRNN网络会将时间大量消耗在计算相关性较小的特征上.

近几年一些学者为更好地学习用户数据信息表征量大的部分，借鉴人类视觉机制提出了注意力机制.注意力机制的核心目标是从众多信息中选择对当前目标更重要的信息，被广泛应用与图像识别[12]，自然语言处理和机器翻译[13]等领域.在推荐领域注意力机制也取得了不错的成果，张全贵等人提出了一种基于注意力机制的音乐深度推荐算法，使深度学习对用户兴趣偏好分析的可解释性增强[14].Zhang等人使用注意力机融合深度神经网络来预测用户转发行为[15].但目前推荐领域引入注意力机制的研究还比较少.

针对上述IndRNN耗时较长且准确率较低的不足，受到注意力机制的启发，给出一种混合注意力机制的独立循环神经网络音乐推荐算法，通过使用注意力机制实现对用户历史收听音乐分配动态权重，从而学习用户的个性化喜好，此外还结合使用散射变换(Scattering Transform，ST)对音频数据进行预处理，以减少音频信息的损失.

2 混合注意力机制的独立循环神经网络算法

音乐推荐算法的任务是为用户推荐喜爱的歌曲，将音乐分为用户喜爱与不喜爱两类，因此，该任务可以归结为二分类问题.混合注意力机制的独立循环神经网络音乐推荐算法(Attention Independent Recurrent Neural Network，AIRNN)是在深度学习RNN的基础上给出的.AIRNN整体混合算法框架如图1所示.

图1 AIRNN混合模型框架图Fig.1 AIRNN model frame diagram

该模型将预测集中的音乐作为输入，输出是预测该音乐是否符合用户的喜好.在训练阶段，首先将训练集分为用户历史收听音频和用户画像两个子部分.其中用户画像由用户收听歌曲语言、用户年龄、收听歌曲类型三部分组成.先将用户历史收听音频通过散射变换得到具有代表性的音频特征，随后将它输入到AIRNN模型中进行特征提取，接着将上述特征池化为单一向量，并同时将训练集的另一部分用户画像通过DNN模型抽取用户特征，同样将上述特征池化为单一向量.将上述AIRNN模型中得到的最终音频抽取特征使用单层网络并通过注意力机制和DNN模型得到的池化后的用户特征相结合，其中注意力机制(Attention)将用户对歌曲的收听次数表征用户对歌曲特征的喜好程度，从而学习用户的个性化权重.最后再次通过归一层(softmax)得到混合音乐推荐模型.

2.1 数据预处理

音频作为一种语音信号无法直接被深度学习网络所使用，且人耳对不同频率的声波有不同的听觉灵敏度，较之高频，人更喜欢低频.针对上述客观事实，学术界通常使用预加重、分帧、加窗、快速傅里叶变换、梅尔滤波器等步骤提取音频信号的梅尔倒谱系数，对音频进行预处理.梅尔倒谱系数(Mel-Frequency Cepstral Coefficient，MFCC)广泛的应用于语音情感识别和音乐推荐算法中.式(1)为MFCC计算公式：

(1)

ψλ(ω)为梅尔滤波器，λ为每一个滤波器的中心频率.

然而，MFCC只有在提取时间尺度为25ms以下的特征时才有效.但500ms以上的信号特征，例如节奏、音色等，对于音乐推荐算法同样重要.因此，使用一种改进的MFCC算法——散射变换(Scattering Transform，ST)提取音频的长时特征，Joakim证明散射变换在音乐推荐算法的预处理阶段中十分有效[16].

散射变换通过小波卷积和模算子级联计算多阶调制谱系数，修复由MFCC产生的信息损失[16].信号x的散射系数为snx，x时不变局部变换为：

s0x(t)=x*φ(t)

(2)

φ(t)为低通滤波器，由于式(2)滤除了所有的高频信号，可以由式(3)小波模组变换修复.

|W1|x=(x*φ(t),|x*ψλ1(t)|)t∈R,λ1∈σ1

(3)

对于连续音频信号，散射变换设定小波和原有的梅尔滤波器具有相同的频率分辨率.由于音频信号在低频时能量极低，因此可以忽略不计.推出一阶散射系数为：

S1x(t,λ)=|x*ψλ1|*φ(t)

(4)

一阶散射系数是由另一个小波模组变换W2计算得出，它补充了高频的小波系数：

|W2||x*ψλ1|=(|x*ψλ1|*φ,|x*ψλ1|*ψλ2)

(5)

通过小波模组系数ψλ2恢复高频信息.这些系数由相同的低频滤波器进行均值得出，由于有第一阶时移不变性作为保证，第二阶散射系数为：

S2x(t,λ1,λ2)=||x*ψλ1|*ψλ2|*φ(t)

(6)

散射系数就像卷积神经网络的结构，可以不停的拓展至第n层[17].

2.2 AIRNN推荐算法

为解决在音乐推荐领域使用RNN算法产生的梯度消失和梯度爆炸问题，在RNN算法的基础上进行改进，得到IndRNN：

ht=σ(Wxt+u⊙ht-1+b)

(7)

ht是时间t时的隐状态，与RNN不同，IndRNN的权重系数由矩阵U变成向量u，权重系数和上一个时刻隐状态的运算变为⊙，即矩阵元素积.式(7)表示在t时刻，每个神经元只接受此刻输入以及t-1时刻的自身状态作为输入,由此可以推导出第n层网络的隐状态：

hn,t=σ(WnXt+unhn,t-1+bn)

(8)

其中，Wn是n维向量的输入权重，un是递归权重.由式(8)可以看出，IndRNN中的每个神经元都可以叠加两层或多层使用，即后一层的每个神经元可以处理前一层所有神经元的输出.Li等人提出的两层IndRNN模型相当于一层激活函数为线性函数、递归权重为可对角化矩阵的传统RNN[18].

通常，RNN是一个参数共享的多层网络，RNN在t时刻每一个神经元都接受t-1时刻所有神经元的状态作为输入[19].与传统的神经网络不同，IndRNN中的每个神经元都可以独立地处理.

(9)

式(9)为IndRNN在t-1时刻反向传播梯度.σ′n,k+1是激活函数的导数，对于第n层神经元，假设目标在是在T时刻的最小化，偏置为0.由于IndRNN中神经元之间相互不起作用，所以IndRNN可以独立计算每个神经元的梯度.与RNN相比，IndRNN的梯度直接由递归的权重决定，而不是矩阵的乘积，并且将激活函数的导数与递归权重系数相互独立.神经元之间的相互连接依赖层间交互来完成，下一层的神经元将会接受上一层所有神经元的输入作为输出.

本文通过叠加IndRNN的基础结构构建一个深度的IndRNN网络，并将网络输入的处理方式由全连接改为残差连接并引入注意力机制，给出一种混合注意力机制的AIRNN音乐推荐算法.算法结构图如图2所示.在每一个时间步长内，借助Relu非饱和激活函数，梯度可以恒等映射并直接传播到其他层.

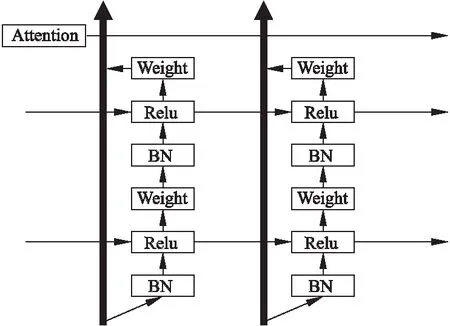
图2 AIRNN推荐算法结构图Fig.2 AIRNN Recommended algorithm structure diagram

问题定义：给定一首歌曲的音频序列M={S1,S2,S3,…，St}，t为音频特征序列的长度.模型的预测问题是给出用户的历史收听列表，并为该用户推荐可能喜欢的歌曲.

用户对这首歌音频序列中第t个音频的喜好函数为ft：

(10)

其中wt为该音频特征对下一首待预测的音乐音频所起作用的权重参数，bt为偏置参数.利用softmax函数将tanh函数所求的f非线性关系进行归一化，得到用户的个性化喜好权重wt：

(11)

音频上下文关系的参数是在训练过程中随机初始化和共同学习得到的.

将用户对整个音频特征序列的个性化喜好权重求和得到权重向量：

H=∑tfuWt

(12)

最后，使用一个二分类器预测下一首歌是否符合用户的喜好.使用一个交叉熵损失函数作为softmax层，将与注意力层结合的音频特征权重向量作为输入，得到预测的结果：

(13)

(14)

Wf和bf为学习参数.通过式(13)、式(14)可以得到一个排名列表，并且将符合用户喜好的音乐推荐给他们.p=[0,1]，将似然函数定义为：

(15)

对式(15)取似然负对数作为损失函数可得的交叉熵损失函数为：

(16)

图3 AIRNN算法流程图Fig.3 AIRNN algorithm flow diagram

AIRNN算法流程图如图3所示.首先按照顺序从歌曲列表中取出数据，并将数据分为音频数据和用户画像两部分，随后把用户历史音乐音频数据进行散射变换，并将从中提取的特征作为AIRNN算法的输入，同时将用户画像数据输入到DNN模型中，将音频数据分析结果通过注意力机制和用户画像抽取出的特征融入相同的归一化层生成列表并记录数据，并判断当前是否将歌曲列表完全遍历.如果记录数量等于歌曲列表数量，便将所得列表排序并推荐给用户；否则返回第一步继续进行上述步骤，直至结束.

3 仿真设计与效果分析

本文在表1的仿真环境下验证了所给出的混合注意力机制的独立循环神经网络算法(AIRNN)，并将AIRNN算法与IndRNN[11]、LSTM[20]推荐算法从不同角度进行对比、仿真结果的分析.

表1 仿真环境Table 1 Lab environment

3.1 仿真数据集与模型训练

仿真所使用的数据集是包含100多万首歌曲元数据和预处理音频特征的集合——百万音乐数据集(Million Song Datasets，MSD)，是目前音乐推荐领域使用最频繁的公开数据集.对比试验主要使用MSD核心数据集中的音乐音频特征和子集Taste Profile所提供的评分数据.

鉴于所选数据集数据较多，为提高模型训练速度，首先按照收听歌曲数目大于200次进行筛选，得到70327名用户数量和283293首歌曲.接着将筛选数据中每一个用户历史收听记录数据分为10份，采用十折交叉验证(5-Fold Cross Validation)将其中的九份作为训练集，其余作为测试集.对比仿真将训练模型的过拟合参数设为0.5，学习率设为设为0.0005.当精度曲线收敛范围稳定时，停止训练并保存模型.

3.2 算法评定指标

推荐系统的评价指标不同于分类算法，较为多元化，有归一化折损累计增益、准确率、满意度等.过高的准确度会使得推荐列表多样性变低，过高的惊喜度和新颖度会使得准确率有所下降，但用户满意度可以直观综合多方面评价推荐系统性能.因此，选取归一化折损累计增益、准确率和用户满意度来对算法进行仿真验证[20].

将算法得出的排名列表取前k，通过准确率可以直观的判断预测结果.准确率定义如式(17)所示.

(17)

归一化折损累计增益(Normalized Discounted cumulative gain，NDCG)通过计算高关联度的排序位置得分情况评价算法，是一个衡量推荐系统性能的重要指标.NDCG定义见式(18).

(18)

其中reli表示第i个结果产生的效益，|rel|表示按最优的方式对结果进行排序.

用户满意度采用问卷调查的方式.其中对指标的重要程度通过使用主观赋权法李斯特量表进行评价，所得的重要性得分作为权重计算的数据，使用得分均值作为原始相对影响系数.问卷共有准确度和惊喜度两个指标，打分等级从1-10，共有10个等级.

调查30名志愿者分别体验基于IndRNN、AINRNN、LSTM三种不同音乐推荐算法，并对其进行打分，取加权和作为每个用户满意度的分数，并取30名志愿者满意度分数的平均值作为算法整体的满意度分数.

3.3 效果分析

首先设置两个仿真实验组对照MFCC和ST预处理对算法的影响，两组使用相同的5层AIRNN网络.从图4中可以看出，在训练达到70个epoch时，使用散射变换预处理的仿真组比使用梅尔倒谱系数的仿真组准确度高15%.这是由于使用梅尔倒谱系数预处理会使音频信息缺失时间尺度为25ms以上的特征，而散射变换可以将损失的特征恢复.因此证明随着可提取音频特征数量的增多，预测的效果也越好，散射变换恢复的长时音频特征捕获到影响用户是否喜欢该歌曲的相关潜在特征.

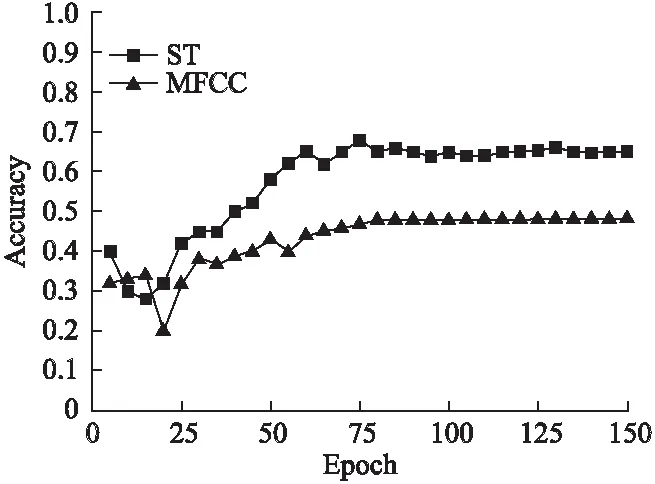
图4 不同数据预处理方式对算法准确度的影响Fig.4 Effects of data preprocessing methods on theaccuracy of algorithm

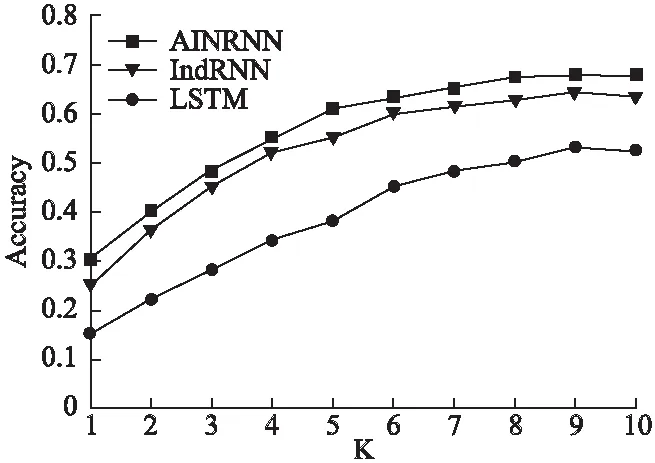
图5 k值对算法准确度的影响Fig.5 Effect of value k on algorithm accuracy

图5展示三种典型神经网络算法AINRNN、IndRNN、LSTM不同k值对算法准确度的影响.当k值小于5时，三个算法的准确度都较低，随着k值增加，LSTM算法准确度始终最低，而IndRNN为65.3%，AINRNN为67.8%，两个算法准确度相差较小.但是在图6中AINRNN的归一化折损累计增益要比IndRNN高7.3%.说明AINRNN可以较好提取音频序列潜在特征，解决了RNN和LSTM梯度爆炸问题，证明该算法应用于音乐推荐领域具有良好的表现.

图6 k值对归一化折损累计增益的影响Fig.6 NDCG effect of value k on algorithm accuracy

同时，随着k值的增大，3个算法准确度的增长趋势为先上升后下降最后趋于平稳.可以看出k值为8-10的时候算法精确度最高.Spotify、QQ音乐等线上音乐服务每日推荐为15首，除去由于商业环境影响一部分歌曲推荐不由音乐推荐算法决定，剩余的歌曲与仿真结果相似.

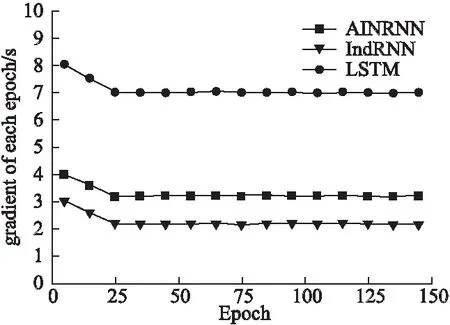
图7 不同算法之间的训练时间Fig.7 Training time between different algorithms

图7中对比AINRNN、IndRNN、LSTM三种算法在音乐推荐系统中的迭代时间.LSTM训练时间最长但效果也最差.IndRNN算法每次迭代的训练时间最短，但是它在图6中的NDCG指标只有50.3%.而引入了注意力机制的AINRNN较

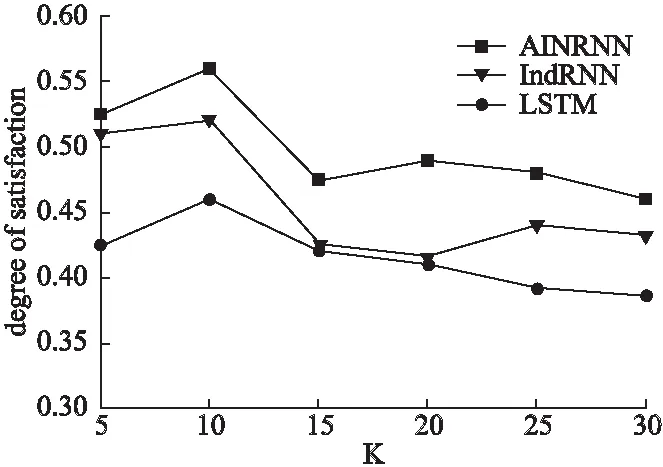
图8 不同算法用户满意度对比Fig.8 Satisfaction on effect of different algorithms

IndRNN损失了1.1s的时间但NDCG指标提升了7.8%.由于目前商业音乐服务的音乐推荐主要为线下推荐，牺牲少量运行速度来换取更高的推荐性能是可接受的.此外，图8显示混合注意力机制的AINRNN算法的用户满意度也最高.由此可以表明所改进的混合注意力机制的独立循环神经网络算法可以很好的应用于音乐推荐领域.

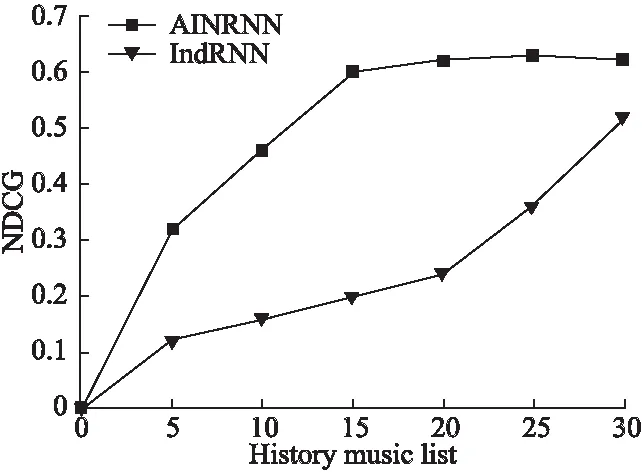
图9 历史收听歌曲数量对算法性能的影响Fig.9 Influence of history songs listened on algorithm performance

探究完k值对算法性能的影响，还要考虑历史收听列表中的歌曲数量是否会影响仿真结果.因此设置了融入注意力机制的AIRNN算法与未融入注意力机制的IndRNN算法作对比仿真，其中k值取10，仿真结果如图9所示.对于MSD数据集，混合注意力机制的AIRNN音乐推荐算法可以在用户历史音乐收听记录仅有16首歌曲时，便很有效地学习用户的个人音乐偏好，与此对照，未融入注意力机制的IndRNN推荐算法只有获取更多的用户历史音乐收听记录(25首歌曲)才能更好地学习用户个性化信息.证明AIRNN推荐算法可以在用户历史收听记录较少时，便可以达到较好的学习效果，从而降低计算复杂度，并且较好的解决冷启动问题.

4 结 论

本文给出一种混合注意力机制的独立循环神经网络算法，并在数据预处理阶段对用户收听历史记录的音频使用改进的梅尔倒谱系数进行预处理.通过在MSD数据集上仿真，结果表明，该算法较比INDRNN算法提升了7.8%推荐准确度和4%用户满意度.与现有模型相比，仿真结果具有较强的竞争力.因此，结合散射变换和AINRNN可以很好地实现在MSD数据集上处理个性化音乐推荐任务.在今后的工作中，将考虑使用内部注意力机制(Intr-attention)有效地利用远距离依赖特征，并平衡惊喜度、新颖性和多样性之间的权重，使推荐性能进一步提升.