切比雪夫逼近的深度神经网络并行加速

李方舒，钱 慧，陈晓旭

(福州大学 物理与信息工程学院，福州 350116)

1 引 言

近年来深度神经网络(Deep Neural Network，DNN)在图像分类，识别，检测等领域取得了巨大的成功.然而DNN普遍存在数据量大，计算复杂度高的问题，在卷积层中尤为突出[1]，这使得网络难以移植到资源有限的嵌入式开发板上.然而随着高科技设备渗透到生活的方方面面，在诸多设备上实现计算密集型的应用变得越来越普遍也越来越重要，因此在资源有限的平台上实现DNN的推理成为了研究者们关注的重点.

为了能在嵌入式终端快速部署DNN，研究者们提出了多种方案.2015年韩松等人[2]提出了去除网络的冗余连接并调整权重以实现网络的压缩，使得网络能够在嵌入式移动应用终端上进行部署.文献[3]通过对网络模型进行压缩与高度优化，将网络从重量级模型变换为能够部署在嵌入式开发板上的轻量级模型，实现了一种基于GPU嵌入式系统的实时驾驶员睡意检测技术.文献[4]通过采用传感器融合超声波来更好的过滤噪声的方法，结合GPU硬件特性，提出了一种基于嵌入式GPU的实时立体视觉碰撞检测自适应系统.文献[5]采用异步多线程并行计算，在GPU嵌入式平台上实现微笑检测器过程中，采用模块化的方案对线程进行优先级排序，并通过增加关键任务的线程数量来实现任务之间的负载平衡.Mohammad的团队针对移动终端上DNN的推理进行了诸多研究[6-8]，发现根据设备的资源量合理的采用不同的线程粒度进行并行化设计能够显著提高网络的推理速度，并提出了数据重新排列，非精确计算等数据处理方案来实现网络的加速设计.面向检测，识别等任务的DNN开始逐渐应用到资源有限的移动设备上.

为了满足人们对高质量，沉浸式影像日益增长的需求，基于深度神经网络的图像重构引起了研究学者的广泛关注[9-12].然而在面向图像重构的DNN中，为了从退化的高维图像中不断提取代表图像细节的关键特征，导致网络各层的输出数据量与输入数据量相同甚至更大，网络卷积层负载情况更为严峻.相较于面向检测识别等问题的DNN，面向图像重构的DNN进行硬件移植时面临着更严峻的挑战.

切比雪夫多项式能够实现最佳的函数逼近[13]，因此本文采用切比雪夫多项式对网络卷积核进行并行化处理以简化卷积层的计算，将该优化方案应用在面向重构的深度神经网络中，随后对优化处理后的网络卷积层进行基于GPU的并行化设计.为了保证方案的普适性，采用zhu等人[14]在2016年提出的基于流形学习的图像重构网络，该网络能够适用于多种不同的图像重构任务.最后将经过并行化设计后的网络移植到NVIDIA AGX Xavier嵌入式开发板上，并对其进行性能分析.

2 面向图像重构的流形学习深度神经网络

基于流形学习的深度神经网络[14]结构如图1所示，传感器数据作为全连接层1的输入，由于传感器数据一般为复数，存在实部与虚部，对于n×n的复杂传感器数据，需将其转换为2n2个实数值输入全连接层1，因此全连接层1也表示网络的输入层，神经元数量为2n2.全连接层2和3的神经元个数均为n2，采用tanh激活函数.为了匹配卷积操作，将全连接层3输出的数据进行维度转换处理，由n2×1变换为n×n.卷积层1采用64个5×5大小的卷积核以1为步长进行卷积操作，卷积层2采用64个5×5×64大小的卷积核以1为步长进行卷积操作.卷积层均采用Relu作为激活函数，最后对卷积层2采用了1个7×7×64大小的卷积核以1为步长进行反卷积得到重构图像.

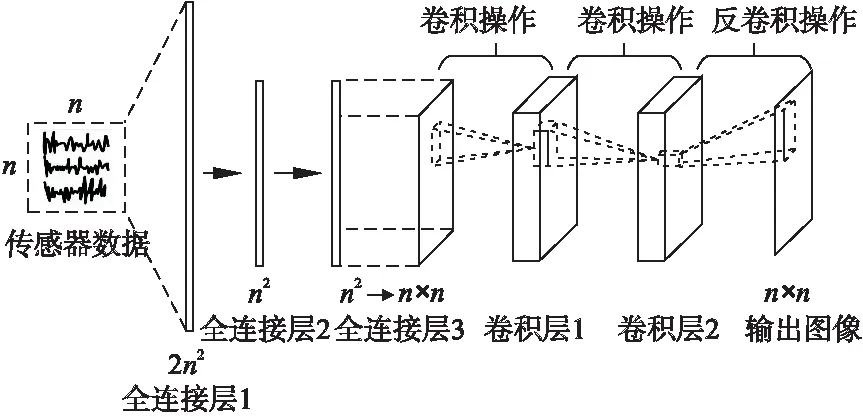
图1 网络结构Fig.1 Structure of the network

DNN中卷积层主要用于实现输入信号高维特征的提取.卷积过程中通过卷积核h对输入数据f进行局部感知，在更高层将局部信息进行综合以提取输入的特征，经典的卷积层计算如公式(1)所示：

y=ξ(h*f)

(1)

y表示当前卷积层的输出，“*”表示卷积操作.ξ表示激活函数，基于流形学习的网络模型中采用Relu函数：

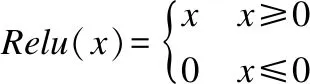
在卷积计算过程中，常常需要四个嵌套的循环，内部在卷积核上迭代，外部在输入图像的行列方向上迭代，循环效率很低.其次，二维图像和卷积核通常采用连续的内存块以行串行化的顺序进行存储，按列访问数据可能会造成内存子系统中较高的高速缓存丢失率，因此卷积操作不容易实现快速计算.考虑采用多项式来对卷积层计算进行简化处理.

3 基于切比雪夫多项式的卷积层优化

3.1 切比雪夫多项式逼近原理

近似计算的核心在于能够在多项式迭代时间内给出问题的近似最优解.而多项式能够实现函数逼近，通过多项式的逼近转换可以将问题转化为对多项式类的研究.且由于多项式的和，差，积仍然是多项式，因此可以通过迭代规律来完成复杂计算的快速实现.

切比雪夫多项式能够实现最佳一致逼近.考虑到实际应用中往往需要对一个已知的复杂函数f(x)进行求解，为了对计算进行化简，通常需要寻找一个函数Qn(x)，使得两者之间的误差能够在某种度量意义下达到最小.切比雪夫最佳一致逼近理论中，函数Qn(x)为切比雪夫多项式，其满足在某区间[a,b]内与f(x)之间的差值是区间内所有多项式Q(x)与f(x)之间插值中最小的，如公式(2)所示：

(2)

3.2 卷积核的切比雪夫多项式逼近

由于切比雪夫多项式能够实现最佳一致逼近，因此考虑采用切比雪夫多项式来进行卷积核的优化.假设输入图像大小为3×3，卷积核大小为2×2(此处为了进行简单的展示，实际上较少出现卷积核大小为2×2的情况).如图2(a)所示，原始的卷积操作中，卷积核大小普遍较小，每次仅能够提取到部分特征，常需要在每个输入特征图上都进行遍历，最后在高维度上进行信息的整合，计算过程复杂.

图2 卷积操作Fig.2 Convolutional operations

本文提出将输入数据表示成向量形式，如图2(b)所示，卷积核中仍然保留对应的权重信息，并采用补0的方式对其进行扩充展开，其中补0 的地方用灰色方块表示.此时卷积核矩阵用H表示，H的维度p×q计算方式如公式(3)、公式(4)所示：

p=((Irow-drow)/stride+1)×((Icol-dcol)/stride+1)

(3)

q=Irow×Icol

(4)

其中Irow和Icol分别表示输入图像的长和宽，drow和dcol分别表示卷积核的长和宽，stride为步长.

此时的卷积计算被展开成为矩阵向量乘法，可以通过一次计算得到结果而无需进行卷积核对输入图像的遍历，且此时输出同样为一个向量，其能够直接作为下一层的输入，无需进行维度转换.

由于卷积操作被展开成了矩阵向量乘法，此时可以对卷积核采用切比雪夫多项式逼近来进行计算化简，以使得其可以进行并行化处理.K阶切比雪夫多项式用Tk(H)∈n×n表示，其递归公式如式(5)所示：

Tk(H)=2HTk-1(H)-Tk-2(H)

(5)

其中T0=1，T1=H.因此卷积核的近似可表示为公式(6)：

(6)

θ=(θ0，θ1，…，θK-1)∈K表示切比雪夫多项式的系数向量，也表示网络中需要训练的卷积核参数.卷积层的输入采用全连接层3直接输出的n2×1维的数据，不进行维度转换，用fin表示，此时网络卷积层计算可用公式(7)表示：

(7)

ycheby表示卷积层的输出.

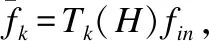
(8)

(9)

3.3 卷积层的并行加速设计

CUDA架构[15]是Nvidia公司推出的GPU异构编程架构，本文结合CUDA 架构对网络卷积层进行并行设计，关键在于切比雪夫多项式迭代的并行设计.

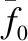
(10)

结合公式(10)和图3可以得出，在第一轮迭代中即可计算得出全部多项式系数，后面每次迭代中对应顺位的多项式系数相等，如图中C(s，0)和C(s，1)所示，将它们按照顺序存储在GPU全局内存(Global Memory)中.

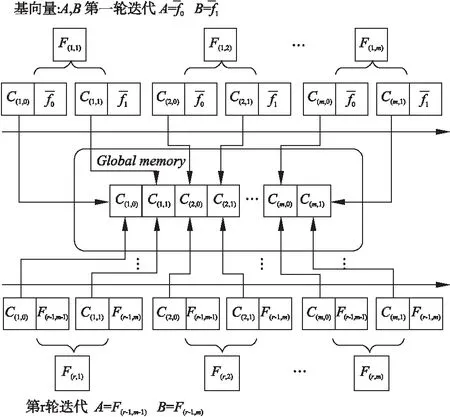
图3 切比雪夫迭代计算流程Fig.3 Process of Chebyshev iterative

在CUDA加速设计时，采用线程并行度为m，在后续迭代过程中直接从GPU全局内存调用提前计算好的对应多项式系数来计算对应多项式的值，从而可以避免每次迭代中多项式系数值的重复计算，也减少了GPU端与CPU端的数据传输次数.图4展示了CUDA进行并行处理的过程，全局内存中开辟出两块内存，一块用于存放计算好的多项式系数，一块存放计算好的多项式的值.迭代计算开始，线程块从全局内存读取多项式系数，为块内线程分配相应的值，每轮迭代结束，采用线程广播机制，将最后两个线程计算得到的多项式值在块内进行广播，作为下一轮迭代的基向量.

图4 基于CUDA的切比雪夫迭代并行设计Fig.4 Cuda-based chebyshev iterative parallel design

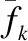
并行度m可以根据硬件平台资源情况进行灵活的设置.由于每轮迭代中所有多项式的计算都在同一时刻进行，每一轮迭代过程中计算时间由两次乘法和一次减法运算得到，因此每次迭代计算所需的时间固定，记为Time1.假设将并行度增大到m+e，所需的迭代次数变为k/(m+e)，增大并行度之后迭代过程中减少的时间为(k/m-k/(m+e))×Time1.与此同时，迭代开始前所需计算的多项式系数个数增加，由2m增加至2(m+e).为了保证增大并行度能够带来计算时间的增益，此时需要关注两点：1)所需计算的多项式系数增加，硬件平台是否有足够的线程资源来支撑它们的计算，而无需等待前面的计算结束并完成资源释放；2)增加的多项式系数计算时间记为Time2，需要保证Time2≤(k/m-k/(m+e))×Time1.通过上述两点的考量对并行度进行设置，可以在硬件上实现资源的充分利用.本文中切比雪夫多项式迭代过程的线程并行度m设置为3.相对于串行的迭代过程，采用并行计算的方式灵活度更高，计算效率能够获得显著提升.

4 实验分析

采用来自MGH-USCHCP公共数据集库[16]医学脑图数据集来进行模型的训练，数据集图片大小处理成64×64.优化前后的网络采用相同的训练环境：CPU为Intel(R)Xeon(R)E5-4610 V4，总内存为15G；GPU为Tesla P100，显存为256G；Tensorflow版本为1.8；CUDA版本为9.0.优化后的网络进行重构验证采用的推理环境：CPU为 Core i7-7700，内存为32G；GPU为Nvidia GeForce GT 730，显存为2G；CUDA版本为9.0.将优化后的模型与原模型进行对比，验证优化后的模型重构性能，采用峰值信噪比(Peak Signal to Noise Ratio，PSNR)来评估重构图像的质量.然后将优化后的模型搭载在Jetson AGX Xavier嵌入式平台上并进行加速效果分析.Jetson AGX Xavier是NVIDIA推出的一款高性能计算开发板，其中支持CUDA 7.0，GPU为NVIDIA Volta架构，CPU为8核 Carmel ARM v8.2，提供了两个深度学习加速器引擎，可提供30TOPs的深度学习运算能力，是目前深度神经网络实现最佳的GPU嵌入式平台.

4.1 网络优化前后计算复杂度分析

DNN的时间复杂度和空间复杂度是评价网络模型架构的重要指标.时间复杂度决定了其进行训练与推理的用时，时间复杂度高时模型训练时间长使得研究者们的想法无法得到快速验证，模型的改善时间也会相应拉长.因此网络的时间复杂度是研究者们关注的评价指标，同时在近似计算中时间复杂度也是一个重要指标.空间复杂度决定了网络模型的参数数量，网络进行硬件移植时需要考虑到硬件平台有限的资源是否能够满足网络部署的要求.

由于DNN中时间复杂度主要来源于网络卷积层，因此主要进行卷积层的时间复杂度分析，公式(11)表示单个卷积层的时间复杂度，其中M表示输出特征图的大小，S表示卷积核的大小，Cin和Cout分别表示卷积层输入和输出的通道数：

ComplexTime=O(M2×S2×Cin×Cout)

(11)

由公式(9)可以得出优化后网络的卷积层时间复杂度仅与该层卷积核参数数量有关，如公式(12)：

ComplexTime=O((S2×Cout)2)

(12)

卷积层的空间复杂度计算公式如式(13)所示：

ComplexSpace=O(S2×Cin×Cout)

(13)

由公式(11)和公式(12)可以计算得出优化前后网络各层的时间复杂度如表1所示.卷积层1和反卷积层为卷积部分的输入和输出层，由于在这两层网络中存在输入或者输出层通道数为1的情况，因此表1中优化后的模型卷积层1和反卷积层的时间复杂度下降不多，但是卷积层2的时间复杂度下降了125.44倍.可以得出通过优化后网络中间隐藏的卷积层的复杂度能够获得明显的时间复杂度下降.

表1 网络优化前后各卷积层时间复杂度Table 1 Time complexity of convolutional layers of thenetwork before and after network optimization

由公式(9)可知，卷积操作被转换为切比雪夫多项式迭代，网络中的参数被转换为多项式迭代中的多项式系数，而此时需要预先计算的多项式系数个数由并行度m来决定，迭代开始前需要计算2m个多项式系数值，因此并行处理后的网络卷积层空间复杂度如公式(14)所示：

ComplexSpace=O((2m)2×Cin×Cout)

(14)

由于m远小于原始卷积核的大小S，因此经过切比雪夫迭代处理后，各卷积核的空间复杂度明显下降.

4.2 优化后的网络模型重构效果验证

优化前后的模型训练方式一致，批次数据量大小设置为100，学习率为0.00002，采用RMSProp算法实现梯度下降，以加快收敛速度.采用均方误差作为损失函数.

图5为训练过程中两个模型损失-迭代曲线图，可以看出优化后的模型起始损失值要大于原始模型，随着迭代次数增加，两条曲线逐渐贴近，最终能够达到相近的重构性能.

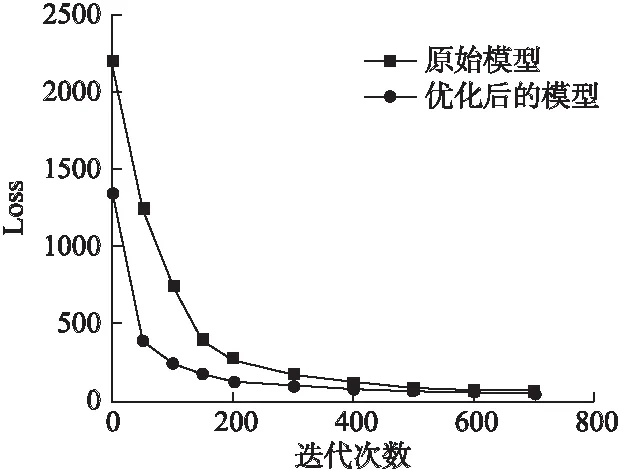
图5 两种模型损失-迭代曲线Fig.5 Loss-iteration curves of the two models

图6中，左边两张图为网络输入图像，右边两张图为优化网络的重构结果，重构出的图像PSNR能达到30dB左右，可以证明优化后的模型可以成功的完成图像重构任务.

4.3 优化后模型的硬件加速实现

实验通过远程交叉编译将模型导入到嵌入式平台上，以文本读取的方式加载权重参数来实现网络的推理过程.采用CUDA中nvprof工具对并行加速设计后的网络模型推理一张图片的过程进行整体分析.网络硬件实现结果如表2所示，显示了warp占用率(AchievedOccupancy，AO)，全局内存负载吞吐量(GlobalMemoryLoadThroughput，GMLT)，全局内存负载效率(GlobalMemoryLoadEfficiency，GMLE)，全局内存存储效率(GlobalMemoryStoreEfficiency，GMSE)，所有参数都取平均值，如公式(15)-公式(17)所示.其中活跃线程数量为n，最大线程数量为Max_threads，请求的全局内存负载吞吐量为GMLT_Q，所需的全局内存负载吞吐量为GMLT_N，请求的全局内存存储吞吐量为GMST_Q，所需的全局内存存储吞吐量为GMST_N.

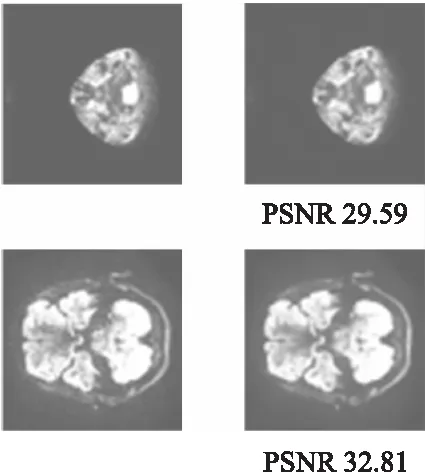
图6 重构结果Fig.6 Reconstruction results

(15)

(16)

(17)

本文基于重构网络进行并行化处理，实验中数据集大小均为64×64，以固定的分辨率图像进行重构.由于完成对网络的并行化设计后，硬件平台上线程调度的方式被确定下来，相应的资源使用方案和计算中的操作数均固定下来，因此对同样分辨率的图像进行重构时，各参数指标理论上保持一致，此处以一张图像的重构为例，对网络的硬件加速情况进行分析.

表2 网络硬件实现分析Table 2 Hardware implementation analysis of network

表2中可以看到激活函数(此处的激活函数为卷积层的激活函数，Relu)的平均占用率最高，达到了83.5119%，表明该核函数中warp的利用最充分.卷积层计算的核函数的全局内存负载吞吐量最高，达到了767.59GB/S，同时全连接层核函数和卷积层核函数的全局内存负载效率、全局内存存储效率都达到了100%，充分利用了设备内存带宽.

由于全连接层1为输入层，因此计算从全连接层2开始.由表3可得，除去网络中各层进行权重矩阵读取的时间，整个网络模型运行时间为0.35s.

表4展示了原始网络在Tensorflow环境下进行推理的时间和并行加速设计后的网络在嵌入式开发板上进行重构推理的时间，可以看出并行加速设计后的网络在嵌入式开发板上进行推理的速度比原始网络在PC端推理的速度快2.2倍.

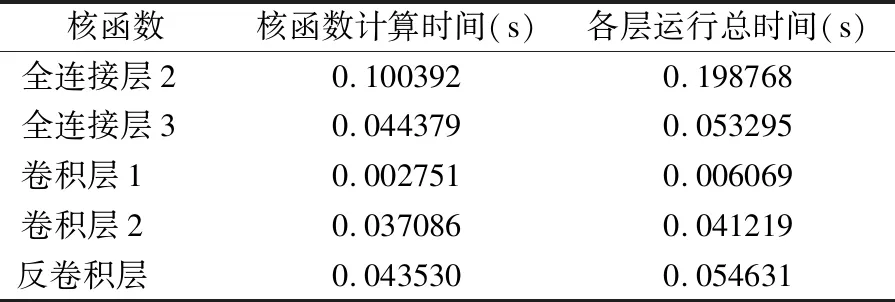
表3 网络运行时间Table 3 Running time of the network

表4 推理时间对比Table 4 Comparison of the inference time

5 总 结

本文针对深度神经网络中数据负荷大，网络卷积层计算复杂度很高的问题，提出采用切比雪夫多项式对网络卷积核进行逼近.通过将卷积核进行展开，使得其与输入数据的卷积操作被转换成矩阵向量乘法的形式，能够无需遍历操作直接计算出卷积结果，然后采用切比雪夫多项式对卷积核中参数进行迭代拟合，使得卷积操作能够实现并行化处理.在网络优化后的基础上，基于CUDA编程架构为卷积层切比雪夫多项式迭代设计了对应的并行加速方案.最后将网络移植到NVIDIA Jetson AGX Xavier嵌入式开发板上，其在开发板上进行推理的时间仅为0.35s.相较于原始网络的推理可以获得2.2倍的加速.