基于RTK-BDS的果园农用车辆自主导航系统研究
2020-10-19郭成洋
郭成洋,张 硕,赵 健,陈 军
(西北农林科技大学 机械与电子工程学院,陕西 杨凌 712100)
0 引言
目前,我国的水果生产在世界上位居前列,截至2016年水果种植面积约为1 725万hm2,各类水果产量约为28 319万t[1]。2019年,中央一号文件对“三农”工作进行了全新的部署,也对果园全程机械化发展提出了更高、更新的要求。自动导航技术作为现代精准农业的一个重要组成部分[2],可以减轻果农劳动强度,提高果园作业效率和质量[3],也是实现果园全程机械化管理的重要途径[4]。
目前,能够提供商业服务的GNSS包括美国的GPS、俄罗斯的GLONASS和中国的BDS系统[5]。Michael O’Connor[6]等人以John Deere 7800拖拉机为研究平台,设计了一套基于四天线RTK-GPS的自主导航系统,试验结果表明:当车辆行驶速度为0.9m/s时,直线跟踪标准差不大于2.5cm。Zachary Pezzementi[7]等人将RTK-GPS应用于苹果园和橘子园的导航定位,实现了果园作业机械的自主行走和自动收获。日本国家农业研究中心[8]将久保田SPU650型水稻收割机进行改装,通过MS750GPS和IMUJCS-7401A提供定位信息,试验结果表明:平均横向偏差小于3cm,最大横向偏差不大于4cm。国内罗锡文[9]等人较早对RTK-GPS导航控制系统进行了研究,将东方红X-804拖拉机进行改装,田间试验表明:控制系统具有较好的精度和可靠性。黎永键[10]等设计了一套基于RTK-DGPS和双闭环转向控制的自动导航定位系统,并以东方红X-804型拖拉机为平台,可将定位平均偏差降低至0.031m。刘军[11]等人设计了一套基于GPS/INS的农用机械自动导航系统,试验表明:该系统定位精度可达0.1m,直线路径跟踪偏差不大于0.27m。
BDS导航系统可在全球范围内为用户提供全天候、全天时的高精度、高可靠性的即时定位服务[12],且该系统完全由我国自主研制,在使用成本和安全性上均优于GPS定位系统,从而得到了广泛关注。为此,结合卡尔曼滤波技术,设计了一套基于RTK-BDS的自适应纯追踪导航控制器,并进行了路径仿真和田间试验,证明导航系统具有良好的精度和可靠性。
1 车辆运动学模型建立
建立整车运动学模型是研究车辆自动导航控制的基础[13]。在实际应用中,果园农用车辆常以低速行驶完成作业工作,因此可以将问题简化为二维平面上的运动描述,并统一考虑农用车辆为前轮转向、后轮驱动形式。为使模型的建立不失一般性及简单性,将轮胎看作刚性轮,在建模中不考虑轮胎由于压力产生的变形和侧向滑移。
基于以上假设,以X-O-Y为固定于地面的惯性坐标系建立农用车辆两轮模型,如图1所示。其中,X-O-Y满足右手法则。

图1 车辆运动学模型Fig.1 Vehicle kinematics model。
由图1可得表达式为
(1)
(2)
式中v—车辆行驶速度(m/s);
vx、vy—车辆沿x轴和y轴方向的速度(m/s);
vp—车辆前轮速度(m/s);
φ—航向角(rad);
δ—前轮转角(rad);
L—前后两轮轴中心的距离(m)。
把式(1)中vp代入到式(2),可以得出二轮车的运动学模型,即
(3)
(4)
式中R—车辆转弯移动半径(m)。
2 基于RTK-BDS的导航控制器设计
2.1 卡尔曼滤波器设计
卡尔曼滤波是一种时域方法,对于具有高斯分布噪声的线性系统,应用该方法可以得到系统状态的递推最小均方差估计[14]。将控制系统视为线性系统,同时将获取的第1个RTK-BDS点作为跟踪轨迹的起点(即平面坐标系的原点)。控制车辆前进运动速度为恒定值,RTK-BDS接收机的采样频率f=5Hz。
设系统的状态向量X为
X=(x,y,vx,vy)T
(5)
(6)
式中x—车辆在平面坐标系内的横坐标值(m);
y—车辆在平面坐标系内的纵坐标值(m);
vx、vy—车辆沿x轴和y轴方向的速度(m/s);
φ—航向角(rad)。
经过离散化后得
Xk=AXk-1+wk-1
(7)
式中Xk—车辆在k时刻被估计的状态量;
A—状态变换矩阵;
wk-1—协方差已知的零均值不相关白噪声。
离散化后的量测方程为
Zk=HkXk+vk
(8)
式中Zk—车辆在k时刻的观测值;
Hk—量测矩阵;
vk—符合正态分布的观测噪声。
vk的值可由式(9)计算得出,即
(9)
式中γk—均值为零的白噪声。
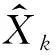
(10)
式中A—状态转移矩阵。
(11)
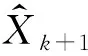
(12)
式中Kk+1—k+1时刻的卡尔曼增益;
Zk+1—k+1时刻的实际观测值。
定义观测矩阵Zk+1可由式(13)得到,即
(13)
k+1时刻的卡尔曼增益可通过式(14)得到,即
(14)
式中P(k+1|k)—k时刻对k+1时刻的预测误差协方差矩阵。
P(k+1|k)的值可通过式(15)得到,即
P(k+1|k)=APkAT+Q
(15)
由于RTK-BDS的定位精度已经可以达到厘米级,因此Q是均值为0的过程噪声协方差对角矩阵。
Sk+1为中间变量,可通过式(16)得到,即
(16)
式中R—观测时的高斯白噪声协方差对角阵,定义为均值0m、标准差1m的对角阵。

Pk+1=(I-Kk+1Hk+1)P(k+1|k)
(17)
2.2 自适应纯追踪导航控制器设计
2.2.1 纯追踪模型
纯追踪模型算法是一种基于几何形学、具有仿生性的算法,通过模拟车内驾驶员的视觉,确定合适的前视距离,计算出车辆到达指定位置所需走过的弧长,从而实现车辆的路径追踪[15]。建立纯追踪模型几何表达示意图,如图2所示。其中,X-O-Y与二轮车运动学模型坐标系相同,即为满足右手法则的完成坐标转换后的大地直角坐标系;点P(x2,y2)为路径上的一点,前视距离Ld为连接车辆重心点A(x1,y1)和点P(x2,y2)弧段的弦长;R为该弧段的半径;Δx为A、P两点的横坐标差值;Δy为A、P两点的纵坐标差值。

图2 纯追踪模型几何表达示意图Fig.2 Geometric expression of pure pursuit model。
由几何关系可得
(18)
由式(18)可得
(19)
结合二轮车模型可得前轮转角δ公式为
(20)
在直线追踪情况下,Δx的计算公式为
(21)
式中d—横向偏差(m);
θ—航向偏差(rad)。
结合式(20)~式(21)式可得
(22)
由式(22)可知:运用纯追踪模型算法进行路径追踪时,其前视距离是固定不变的。Conlter[16]等在研究中发现:当前视距离取值过大时,会使车辆沿小弧曲线逼近设定路线,耗时较长;前视距离取值过小时,会使车辆沿大弧度曲线逼近设定路线,使系统产生较大振荡。为此,本文提出采用模糊自适应纯追踪算法来实现车辆的路径追踪。
2.2.2 模糊控制器设计
模糊控制模仿人脑对不确定性概念进行判断和推理,适宜解决非精确数学模型的复杂控制系统的控制问题[17]。由于前视距离的大小受横向偏差和航向偏差两因素双重影响,故本文将横向偏差与航向偏差作为模糊控制器的输入,前视距离作为输出。当横向偏差与航向偏差较大时,使用较小的前视距离使车辆快速逼近跟踪路径,减小系统调节时间,提高系统响应速度;当横向偏差与航向偏差较小时,使用较大的前视距离,防止系统超调,提高系统稳定性。
选用高斯型隶属函数,其表达式为
(23)
其中,参数σ用于决定曲线的宽度;参数c用于决定曲线的中心。
对横向偏差、航向偏差和前视距离进行模糊化,横向偏差模糊论域为[-0.5,0.5](单位为m),航向偏差模糊论域为[-π/2,π/2](单位为rad),前视距离的模糊论域为[0,6](单位为m),三者均划分为13个等级,用{-6、-5、-4、-3、-2、-1、0、+1、+2、+3、+4、+5、+6}表示。同时,规定车辆位于导航线右侧时横向偏差为负,左侧为正;航向偏差顺时针为正,逆时针为负;分为7个模糊集:负大(FB)、负中(FM)、负小(FS)、零(Z)、正小(ZS)、正中(ZM),正大(ZB)。最后,利用MatLab工具箱绘制出输入输出隶属度函数曲线如图3~图5所示。

图3 横向偏差隶属函数Fig.3 Lateral deviation membership function。

图4 航向偏差隶属函数Fig.4 Heading deviation membership function。
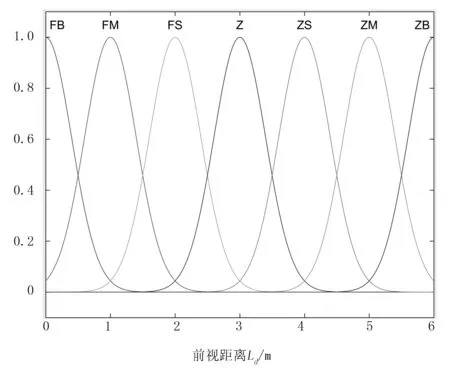
图5 前视距离隶属度函数Fig.5 Forward vision distance membership function。
利用专家经验建立49条模糊规则如表1所示,利用MatLab工具箱绘制了模糊控制曲面如图6所示。

表1 模糊控制规则表Table 1 Fuzzy control regulation table。

图6 模糊控制曲面Fig 6 Fuzzy control surface。
通过模糊推理得到的结果是一个模糊集合,但在实际应用中必须要有一个确定值,才能控制或者驱动执行机构。本文选用重心法进行反模糊化,即
(24)
式中v0—输出值;
V—输出论域;
μv(v)—输出的模糊集合。
3 仿真与田间试验
3.1 MatLab仿真
将简化二轮车模型、模糊控制模型和纯追踪模型,跟踪路径在MatLab/Simulink中搭建,仿真主程序如图7所示。

图7 导航系统Simulink仿真主程序Fig.7 Simulink model of navigation main program。
在仿真过程中设定起始点为(0,-5)(单位为m)处,初始航向角为0°,行驶速度为0.5m/s,固定前视距离取车辆2~3s走过的距离为1.3m,车轮距为1.6m。该参数来自实验室SH-GL型电动车,直线跟踪路径为y=x。直线追踪不同算法对比如图8所示。

图8 直线追踪不同算法误差对比图Fig.8 Straight line tracking different algorithm error comparison chart。
仿真结果表明:直线跟踪时,固定前视距离算法的横向偏差最大超调量为0.399m,航向偏差最大超调量为0.092rad,达到稳态的时间为47s;自适应纯追踪算法的横向偏差最大超调为0.314m,航向偏差最大超调为0.106rad,达到稳态的时间为36s。超调量总体较大的原因是由于起始点位置选取与跟踪路径起始点位置相差较远造成。综上所述,自适应纯追踪算法具有较快的响应速度和较好的调节精度,可以满足果园农用车辆的实际作业需要。
3.2 田间试验
为了验证自适应纯追踪算法的精度,以双辉车业有限公司生产的SH-GL型电动车作为试验平台,试验选择在西北农林科技大学校内的水泥路面上进行。为了模拟果园环境,道路两旁种有株间距为3m,行间距为5.5m的16株树木,试验场景图像如图9所示。

图9 田间试验场景Fig.9 Field trial scene。
在田间试验开始前,调整车辆行驶速度为0.5m/s,并连结由RTK-BDS导航定位系统静止采集得到的起点和终点转换坐标,从而形成试验所需的直线目标追踪路径。试验中选用的传感器型号如表2所示。

表2 主要传感器选型Table 2 Main sensor selection。
选取不同的起始点进行5次试验,以RTK-BDS实时采集到的车辆位姿坐标来计算横向偏差,统计结果如表3所示。
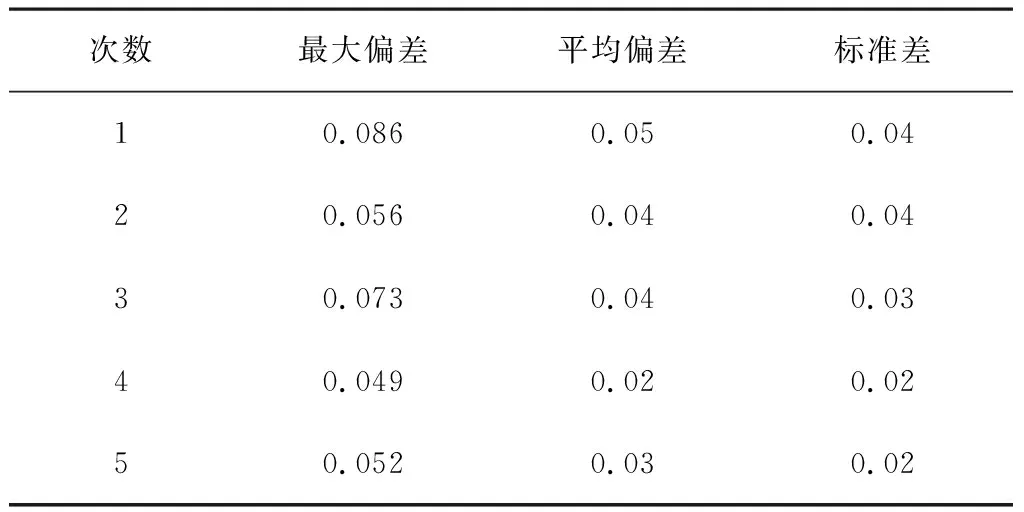
表3 横向偏差统计结果Table 3 Statistical results of lateral deviation m。

续表3。
由表3可知:经过5次试验后,最大横向偏差为0.086m,最大平均偏差为0.05m,最大标准差为0.04m;最大偏差平均值为0.063m,平均偏差平均值为0.036m,平均标准差为0.03m。试验表明:基于RTK-BDS的自适应纯追踪算法具有较好的导航精度,可以满足果园农用车辆的实际作业需要。
4 结论与展望
使用RTK-BDS接收机实时提供的导航定位数据,采用卡尔曼滤波算法和自适应纯追踪控制方法,实现了果园农用车辆的直线跟踪导航控制。试验表明:在前进速度为0.5m/s时,直线跟踪的最大误差不大于0.086m,平均跟踪误差不大于0.036m。
本文中只考虑了果园农用车辆定速直线路径追踪的情况,未考虑地头转弯和不同工况下不同行驶速度对路径追踪效果的影响,还需要进一步的研究。
