基于改进K均值特征点聚类算法的作物行检测
2020-10-19孟笑天徐艳蕾王新东翟钰婷
孟笑天,徐艳蕾,2,王新东,何 润,翟钰婷
(1.吉林农业大学 信息技术学院,长春 130118;2.吉林大学 工程仿生教育部重点实验室,长春 130022)
0 引言
精准施药技术是精准农业的一个重要组成部分,能够减少对生态系统的破坏,保障人类的生命健康安全[1-2]。精准施药是通过空间传感技术采集并解析具有地理位置的农田作物长势、病虫草害等农作物信息,再依据不同的农情制定不同的喷雾方案,按需喷药,实现无人操作。而在精准施药的过程中,作物行检测是关键环节,很大程度上影响农业机械的视觉导航效果和施药的精准度。目前,常用的作物行检测算法有霍夫变换法(Hough transform, HT)[3]和最小二乘法[4]。霍夫变换法鲁棒性强且抗干扰性好,但也存在计算量大、内存需求高等不足。近年来,很多学者在基本霍夫变换的基础上进行改进,提出优化的霍夫变换方法。Jiang 等[5]提出了霍夫变换与消隐点约束相结合的算法,运用移动窗口的方法来提取代表作物行的特征点,并利用霍夫变换算法检测出大于实际作物行数的候选直线,最后基于消隐点的方法得到真正的作物行。Xu等[6]提出随机霍夫变换,以多对一的映射方式减少数据计算量,采用动态链表降低内存。但是,上述方法在实时性和精确度方面仍存在不足。最小二乘法作为一种数学优化技术,速度快是区别于其他方法的一个显著优势。司永胜等[7]提出基于最小二乘法的早期作物行中心线检测算法,利用特征点的邻近关系对目标点分类,对点集里的特征点用最小二乘法进行直线拟合。但是,最小二乘法对噪声敏感,导致对直线的拟合效果有很大影响。
针对上述方法的不足,提出一种改进K均值聚类算法,以苗期玉米为研究对象,将作物行中心线候选点集进行分类,再采用最小二乘法提取作物行中心线,以期能够提高作物行检测的精确度。
1 图像获取与预处理
1.1 图像获取
本文所用的玉米图像均取自于吉林农业大学科研试验田。采用陕西维视数字图像技术有限公司生产的 MV-EM040M工业相机,配有可变焦距的C口镜头,能够对自然环境下的玉米作物行图像进行采集。相机距地面高度约为1.6m,输出8位RGB彩色图像。试验计算机环境配置为CPU主频2.4 GHz,RAM为8.0 GB。图像处理所用的软件平台为MatLab R2014a。
1.2 图像预处理
1.2.1 灰度化
获取原作物图像[见图1(a)]后,为了更好地将作物图像与背景分离,在常规超绿法(excess green)[8](即2G-R-B特征因子的基础上)减小绿色分量的比例因子,对图1(a)进行灰度化处理得到图1(c)。常规超绿法处理结果如图1(b)所示。对比处理后的图片可以看出:改进的超绿法使作物行更突出,分离效果更好。

图1 常规超绿法与改进超绿法灰度化Fig.1 Conventional super green method and improved super green method graying。
1.2.2 二值化
为了进一步将作物行与背景分离,提取作物行相关信息,需要进行二值化处理。Otsu作为最为常用的图像分割方法[9],可以自动确定分割阈值,且计算方法简单、适应性强。因此,采用Otsu算法对图像进行二值化处理,如图2所示。

图2 Otsu二值化图像Fig.2 Otsu binarized image。
1.2.3 特征点提取
为了减少下文聚类算法的计算量,减少噪声点的影响,本文采用左右边缘中间线检测算法[10]从图2中提取代表作物行的像素点,如图3所示。

图3 特征点图像Fig.3 Feature point image。
2 K均值聚类算法基本原理及改进
2.1 基本原理
K均值聚类算法是最早由J.B.MacQueen提出的一种基于划分的聚类方法,其具有简单和高效的特点,在各个领域得到广泛应用。K均值聚类算法首先从原始的数据集中随机选择K个数据点作为初始聚类中心(也称簇中心);然后计算数据集中其它数据点与每个初始聚类中心的距离,根据距离大小将其划分到与之最近的类中;再计算各类中所有数据点的平均值,调整各类的聚类中心,更新其它数据点的所属的类;如此反复迭代,直至目标函数收敛。通常目标函数采用均方差定义,则
(1)
式中k—聚类的个数;
x—原始数据集中任意1个数据点;
ci—1个类(簇);
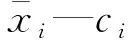
2.2 改进K均值聚类算法
K均值聚类算法虽然原理简单、运行效率高,但需要事先已知聚类的个数K,且初始聚类中心的随机性容易使算法陷入局部最优,从而导致分类效果不理想。针对上述问题,从确定聚类个数和选择初始聚类中心两个方面进行改进,以提高聚类的效果。
2.2.1 聚类个数的确定

(2)
式中L1—平均类间距离;
k—聚类数目;

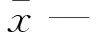
(3)
式中L2—平均类内距离;
k—聚类数目;

x—类ci中的数据;
n—原始数据集的数据个数。
L(k)=L1-L2
(4)
2.2.2 初始聚类中心的选择
为了克服随机初始聚类中心对K均值算法的影响,本文提出改进的选择方法。首先,计算出原始数据集的中心X1,并将其作为第1初始聚类中心;然后,根据点密度公式(5),在r∈(0,d)范围内,计算X1的点密度D(X1)。当点密度最大时,在对应的领域内选取距离X1最远的数据点作为第2初始聚类中心X2,并且除去X1、X2,再重复上述步骤,得到第3初始聚类中心X3;不断迭代,直至获取k个初始聚类中心。
D(xi)={x∈X|dist(xi,x)≤r}
(5)
式中D(xi)—xi的点密度,即处在点xi的r邻域内的点的数量;
xi—聚类中心;
X—原始数据集;
x—数据集内的任意对象;
r—领域半径,r∈(0,d),d为在数据集X中聚类中心与离它最远数据点的距离。
通过改进方法获取初始聚类中心,保证了算法的迭代起点更接近于真实的聚类中心,减少了迭代的次数,提高了算法的执行效率。
3 基于改进K均值特征点聚类的作物行检测
3.1 基于改进K均值算法的特征点聚类
作物图像经过1.2节的图像预处理后,获得可代表作物行的候选特征点,如图3所示。下一步采用改进的K均值算法对候选特征点进行准确的聚类,使得代表每个作物行的特征点划分为相应的类。算法的具体步骤如下:
1)从上到下,从左到右,找出所有像素值为1的特征点,统计其数量n。

3)计算所有特征点的平均值X1(即中心点),作为第1初始聚类中心,根据式(5)计算X1的最大点密度所对应的邻域半径r。在该邻域半径内,找出距离X1最远的点X2作为第2初始聚类中心并删除点X1。得到X2后,重复上述步骤直至找出第k个初始聚类中心Xk。
4)根据式(1)计算所有特征点到各聚类中心的欧式距离,并将其划分到距离最近的类中。
5)根据式(6)更新聚类中心。
6)判断目标函数是否满足收敛条件,即|E-E′|ε。其中,E为本次的目标函数值,E'为上次迭代的目标函数值。若不满足,转至4)、5)继续迭代;若满足,算法结束。
(6)
式中nj—第j类中的特征点个数;

xi—第j类中的特征点。
为了便于比较改进算法与传统算法的聚类结果,基于MatLab软件将图片背景设为白色,并用不同的符号对每一类特征点进行标记。改进K均值算法和传统K均值算法的特征点聚类结果如图4所示。由图4(a)可以看出:作物行特征点被清晰地划分为5类,每一类代表1个作物行;而传统K均值算法聚类后的图像只有2~3个作物行特征点被准确地分类。由此可见,改进的K均值聚类算法对作物行特征点的划分效果更好。


图4 两种算法对特征点聚类的结果Fig.4 The result of clustering of feature points by two algorithms。
3.2 最小二乘法直线拟合
最小二乘法是一种常用的数学优化方法,用于直线检测准确度高且速度快。根据3.1节得到的作物行特征点图像,采用最小二乘法分别对每一类作物行特征点进行直线拟合,拟合结果如图5所示。

图5 作物行中心线检测结果Fig.5 Crop line centerline test results。
4 试验与分析
为了验证本文算法对不同天气状况和光照强度的适应性和效率,选取200幅玉米的苗期图片。其中,100张为天气晴朗、光照强的图片,剩余100张为阴天、光照弱的条件下拍摄。分别采用改进的K均值算法和标准霍夫变换算法进行作物行中心线检测,试验结果如表1所示。

表1 两种作物行检测算法的性能对比Table 1 Performance comparison of two crop line detection algorithms。
由表1可以看出:不管在晴朗、光照强还是在阴天、光照弱的拍摄条件下,相对于标准霍夫变换算法,改进的K均值算法均有较高的识别率,整体识别率达到91%。为了进一步说明本文算法的效率,采用Jiang等[12]提出的误差计算方法,以原作物图1(a)为例,通过手工绘制作物行的参考直线(参考直线尽可能无限接近作物行的中心线),如图6中粗线所示;然后,分别计算参考直线与改进K均值聚类检测直线[图6(a)中细线所示]、霍夫变换检测直线[图6(b)中细线所示]的夹角,夹角越小,检测算法的精确度越高。经过试验,霍夫变换算法和改进K均值算法的平均误差分别为2.103 5°、1.141 1°。这说明,改进的K均值聚类算法对作物行特征点分类的效果更好,检测直线平均误差更小,具有较高的检测精度。

图6 两种算法检测直线与参考直线对比Fig.6 Two algorithms detect line and reference line contrast。
5 结论
1)为了更加准确地检测作物行,在深入研究传统K均值聚类算法的基础上提出改进:首先,根据距离函数最值关系求出最佳聚类数目;然后,依据点密度大小和邻域半径确定初始聚类中心,减少了迭代次数,提高了算法的执行效率和划分效果。
2)采用改进的K均值聚类算法对作物行特征点进行聚类,并采用最小二乘法进行直线拟合,提高了直线拟合的效果,总识别率为91%,高于标准霍夫变换的82%;且改进的K均值聚类算法和标准霍夫变换的平均误差分别为2.103 5°、1.141 1°。试验数据表明:提出的基于改进的K均值特征点聚类算法识别效果好,精确度高,可为精准施药提供理论依据。
