基于ANSYS的压力容器应力分析设计方法
2020-10-19赵亮
赵亮
锦西化工机械集团有限公司,中国·辽宁 葫芦岛 125001
应力分类法;极限载荷法;弹塑性分析法;应变限制
1 引言
压力容器的分析设计,首先进行载荷分析,确定结构的载荷形式、量级、作用区域和波动范围,诸如内压、外压、重力、惯性力及载荷循环次数。其次进行结构分析,确定应力分析部位和构造力学模型(包括力学和位移的边界条件),确定材料的本构关系,确定分析设计方法和结果处理方法[1]。
结构分析中的自由度是位移,热分析中的自由度是温度,为保证求解需要限制刚体的位移约束,诸如轴向位移约束、对称约束和环向位移约束。
实施完整的压力容器分析设计的一般过程如下:
分析设计条件的提出—载荷分析—材料选择—结构设计—总体强度尺寸确定—局部结构强度尺寸初定—分析模型构建—应力分析—强度评定(通过)—技术说明—技术要求—图样绘制—设计文件整理。
2 分析设计方法
分析设计方法一般分为应力分类法和直接法[2],如图1所示。
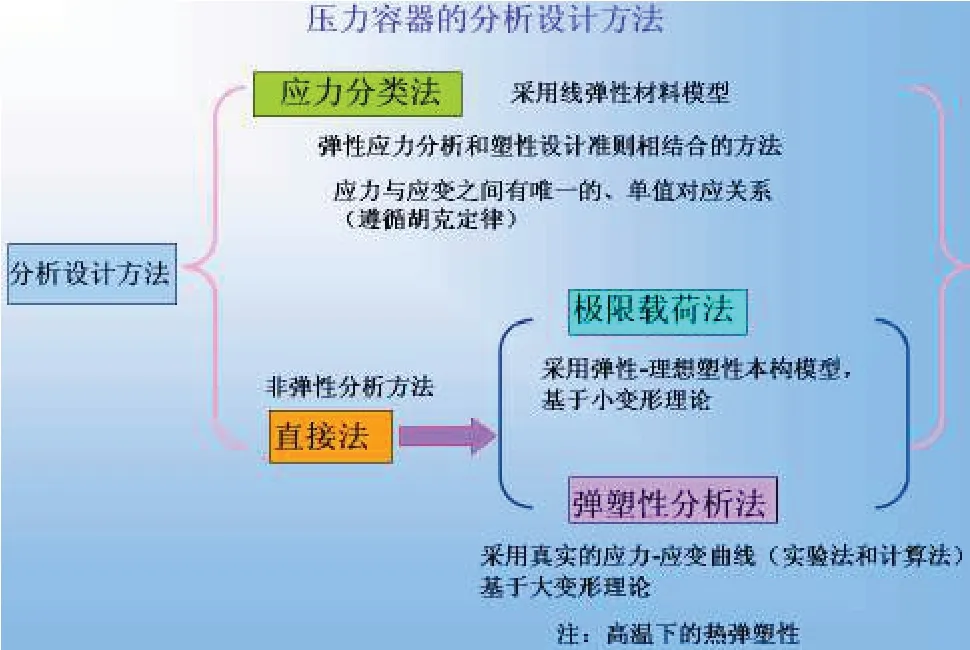
图1 压力容器的分析设计方法
2.1 应力分类法
应力分类法是我们熟知的一种方法,基于JB4732 标准的应力分类的分析设计是对总体结构采用弹性力学的分析结果计算结构应力,采用第三强度理论计算结构当量强度。在按总体结构强度设计的基础上,重点将强度设计放在局部不连续结构的强度设计上。引入应力分类的概念,根据引起应力的原因和对结构强度影响性质不同对结构应力进行分类。对不同类型的应力限制标准不同。
应力分类法要求区分五类应力:一次总体薄膜应力Pm;一次局部薄膜应力PL;一次弯曲应力Pb;二次应力Q;峰值应力F。
控制上述各种应力及其组合的目的是:
(1)控制一次应力极限是为了防止过分弹性变形,包括稳定在内。
(2)控制一次应力与二次应力叠加的极限,是为了防止过分的弹性变形的增长性破坏——不安定。
(3)控制峰值应力极限的目的是防止由周期性载荷引起的疲劳破坏。
其中,评定方法按JB4732 标准表5-1 和5.3 条的要求进行评定:
(1)一次总体薄膜应力强度SI的许用极限为KSm。
(2)一次局部薄膜应力强度SII的许用极限为1.5KSm。
(3)一次薄膜加一次弯曲应力强度SIII的许用极限为1.5KSm。
(4)一次加二次应力强度SIV的许用极限为3Sm。
2.2 极限载荷法
采用极限载荷法时[3],在分析中采用小位移理论的弹性-理想塑性材料模型,应用von Mises 屈服准则和关联流动法则,以屈服强度等于1.5S 来确定塑性极限(S 为材料的许用应力)。
采用的双线性模型是通过两个直线段来模拟弹塑性材料的本构关系,即认为材料在屈服以前应力—应变关系按照弹性模量成比例变化,屈服以后,按比弹性模量小的另一个模量(切线模量)变化。 模型有两个斜率:弹性斜率和塑性斜率。在极限载荷分析中,由于采用弹性-理想塑性模型,所以塑性斜率为零,因此模型中只需要定义弹性模量和屈服强度。
!极限载荷法材料模型


采用极限载荷法的评定:
依据ASME VIII-2 用于极限载荷分析的载荷组合工况和载荷系数,只考虑内压P 时查得总体准则载荷系数为1.5,局部准则载荷系数为1.7。因此,总体分析时施加载荷为1.5*P,局部分析时为1.7*P。如果模型结果收敛,元件在此载荷工况下是处于稳定的,因此不会发生塑性失效,评定合格。
需要注意的是:
(1)除温度载荷外的其它所有载荷均按比例加载。
(2)若给定位移边界条件,则位移应等于零。
(3)不计及热负荷和规定的非零位移。
极限载荷法中极限载荷的获得:
按“载荷与抗力系数”加载,如果结果收敛,只是表明结构在设计载荷下是安全的,但并不能求得结构最终的极限载荷。如果需要求得结构的最终的极限载荷,则可以按比例加大设计载荷,使结构在TIME<1 时不再收敛,以施加的载荷乘以TIME 值即可求得结构的极限载荷,再除以“载荷与抗力系数”得出结构的许用极限载荷,如图2所示。
那么如何绘制分析结束后的载荷-应变曲线呢?相应命令流如下:



图2 极限载荷法的载荷-位移曲线
极限载荷法分析,求出极限载荷 Ps,对于一次加载当给定载荷≤ 2*Ps/3 则可替代SⅠ、 SⅡ、SⅢ三项的评定。
极限载荷分析对弹性分析和应力线性化以及应力分类中的一次应力极限提供了另一种选择。由极限载荷分析解所表示的位移和应变并无物理意义。由于极限载荷是根据极限状态时结构的平衡要求确定出来的。因此,自平衡力系对极限载荷没有影响。自平衡力系包括焊接应力、装配应力、初始残余应力、热应力。
采用Mises 屈服准则求出的极限载荷≥由Tresca 屈服准则求出的极限载荷,但不会超过1.15 倍。
2.3 弹塑性分析法
采用真实的应力-应变曲线模型,真实的应力-应变曲线的获得需要依据Asme VIII-2 附录3-D 所提出的考虑材料塑性应变强化的本构模型[4],只要知道材料的屈服强度、抗拉强度、弹性模量及断后延伸率(标准保证值和实测值),就可以获得材料的真实应力-应变曲线,用于弹塑性分析的有限元数值求解中。这需要编程实现。 真实的应力-应变曲线程序如图3所示。

图3 材料的真实应力-应变曲线程序
弹塑性分析中的材料模型输入:应力-应变数据按照程序计算的输入即可。
第一:多线性等向强化(MISO)的命令流:

第二:多线性随动强化(MKIN)的命令流:


如图4所示,在弹塑性分析中,除了要防止总体塑性失效外,还应防止局部失效。前面介绍过,弹性分析校核局部失效时,采用局部一次薄膜应力加弯曲各主应力的总合,三个主应力之和不大于4S。而在弹塑性分析中,防止局部失效由应力控制改为应变控制。
EN13445 规定弹塑性分析时,操作工况主结构应变的绝对值≤5%;试验工况时≤7%。ASME 标准并未给出应变限制的具体数值,但给出了应变限制公式。

图4 弹塑性分析的局部失效分析过程
提到了应变限制,再说一下分析体会。在应力分析设计中,对不同类型的应力所得的应力强度,分别采用极限设计和安定性的观点予以评定,在此实质上是允许应力超过屈服强度的。极限设计的观点是结构一点进入屈服后结构仍然具有承载能力,直至整个截面或局部区域进入屈服,结构才达到承载极限[5]。安定性的概念是允许结构在承受第一次加载循环时产生一定量的塑性变形,但在以后的加载过程中不会产生累加的塑性变形。由此,分析设计的结果评定是允许结构进入塑性状态的评定,因此实质上评定是采用应变进行控制的。但在实际结果评定中均将相应的应变转换为当量的虚拟应力来加以限制。这样在实际应力分析中,就可假设结构处于弹性状态来处理问题了。因此一般应力分析按弹性分析处理即可——实质上是应变控制。
相关的应变限制在标准中有详细介绍:第一:EN13445要求的是操作工况下主应变小于5%;压力试验工况下主应变小于7%。第二:ASME III-NH 标准中的非弹性分析法基于应变限制的评定为:薄膜应变<1%;弯曲应变小于2%;局部应变小于5%。第三:国内新版的压力容器分析设计标准中征求意见稿里的二元准则规定,变形准则按照总应变小于5%。强度准则按照ASME 的总体准则,载荷抗力系数取2.4 时,结构计算收敛。
2.4 举例论证
2.4.1 罐式集装箱框架的结果评定
安定性要求当结构的弹性名义应力小于等于两倍屈服极限,即:σ ≤ 2σs。
如果结构在载荷、温度等反复变化的过程中,只是在最初的循环过程出现一定的塑性变形,而在以后的各次循环中不再出现新的塑性变形,也无塑性变形的积累,这时就称结构是安定的。
因此,当ANSYS 分析移动式压力容器的C3 类罐式集装箱的堆码试验(顶部四个角件分别施加848000N)时,一般采取梁壳单元建立模型,分析结果直接给出了结构的应力和应变,无需线性化处理。框架的最大总应力值可以大于材料的屈服强度,但一般小于两倍的屈服强度,此时结构是安定的。当材料进入屈服阶段后,失效模式与应变的相关性较大,用应变作为判据更合适[6]。因此,可以采用输入材料的屈服极限,采用小变形理论,线弹性理想塑性材料本构关系,Mises 屈服极限及相关联的流动准则,对堆码试验工况进行分析,对分析结果中的框架查看mises 当量塑性应变,要求当量塑性应变的最大值<1%,按照1%来评定,结果偏保守。则可认为结构安定到弹性行为。
按照弹性分析(胡克定律)的框架结果为494.98Mpa(大于Q345E 材料的屈服强度345Mpa,小于两倍屈服强度),如图5所示。
按照非弹性分析,采用理想弹塑性材料模型,分析结果的当量塑性应变为0.00323,小于1%,评定合格,如图6所示。
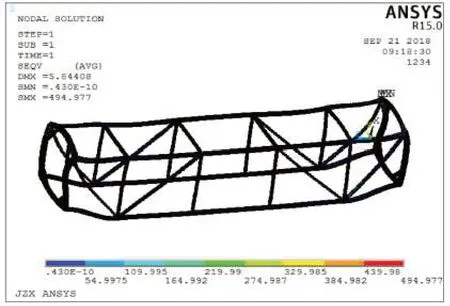
图5 框架堆码试验时的Von-Mises 等效应力云图
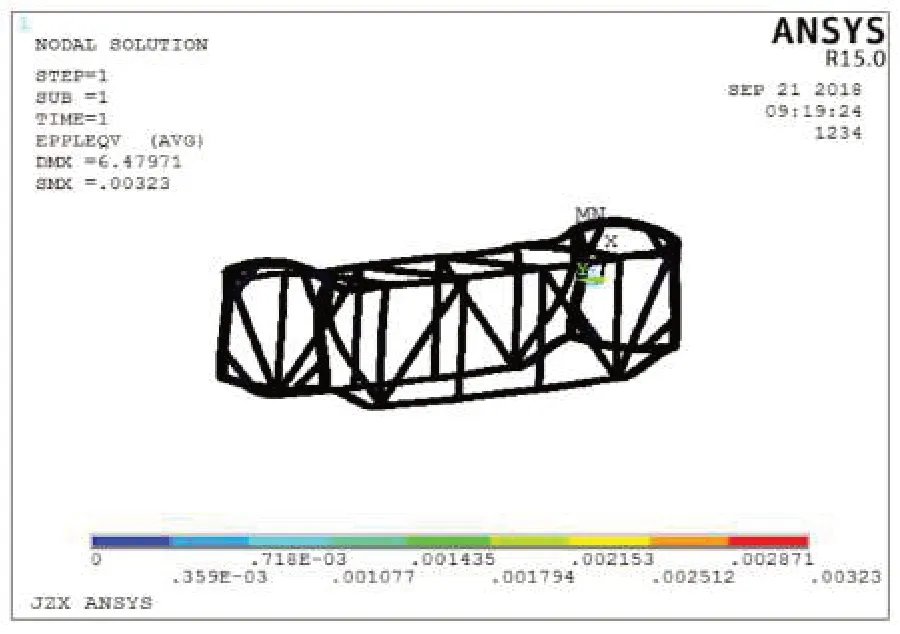
图6 框架堆码试验时的当量塑性应变云图
2.4.2 其他非受压元件的结果评定
应变评定方法还可以包括其他非受压元件的评定。诸如下面的试压平盖,在平盖上端加固井字形钢板,其应力云图如图7和图8所示。加强结构的等效应力为548MPa,超过屈服345MPa。查看塑性应变为0.0087,小于1%,评定合格,如图9所示。
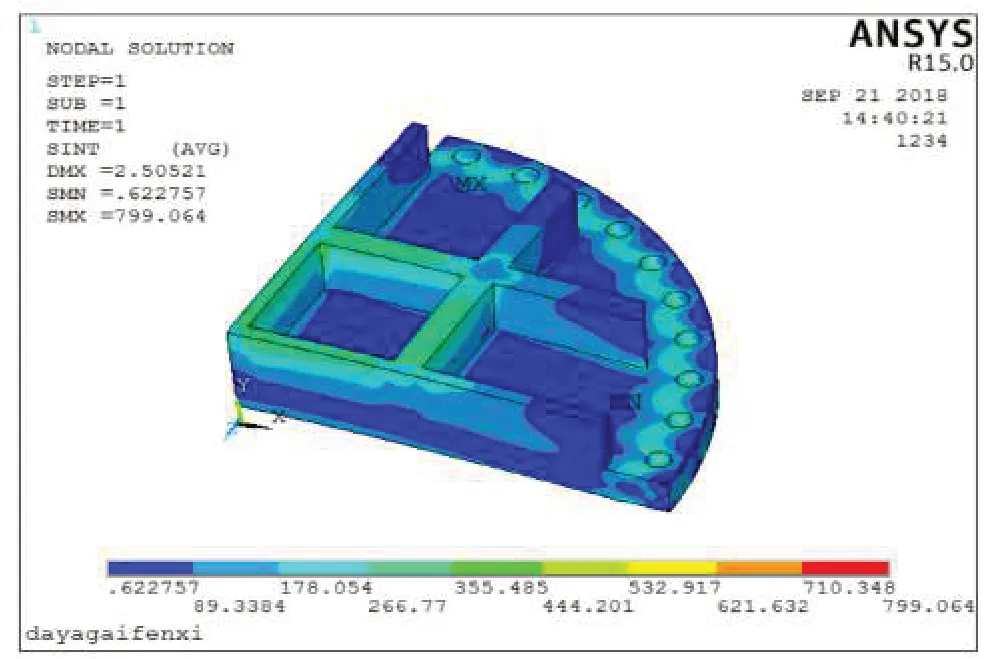
图7 试压平盖整体应力云图
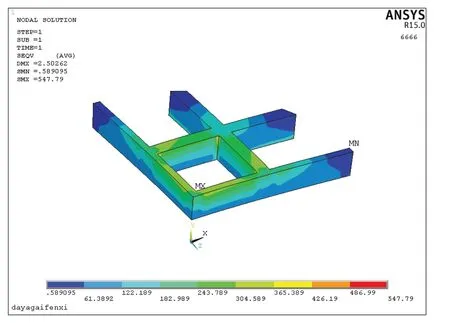
图8 试压平盖加强结构的等效应力云图
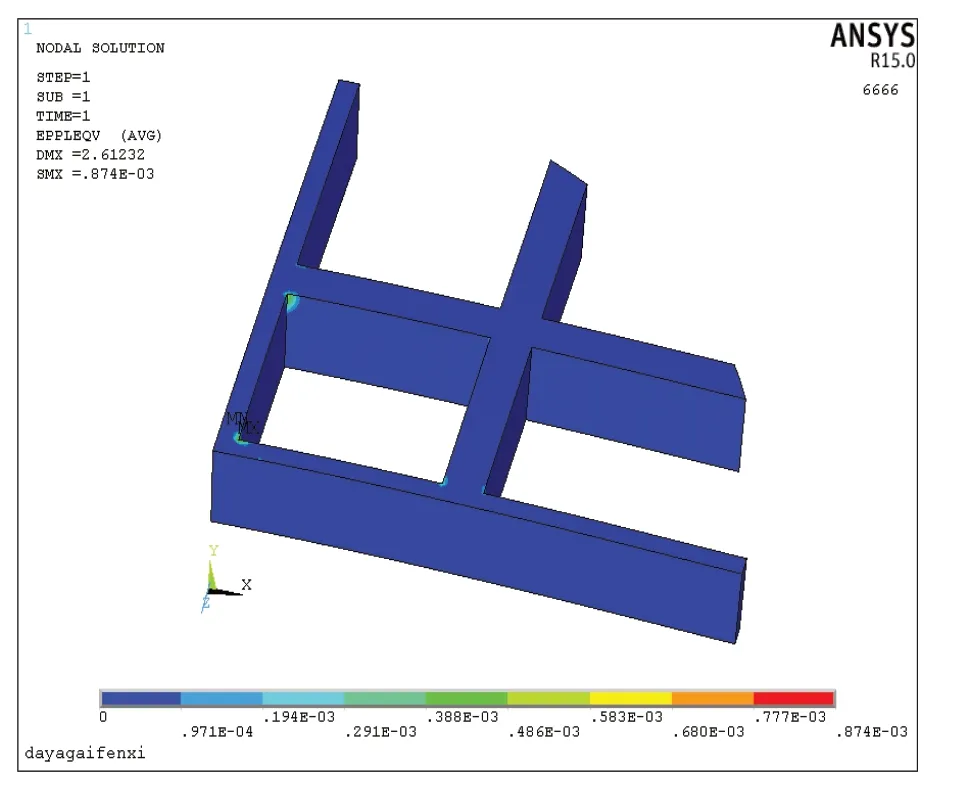
图9 试压平盖加强结构的当量塑性应变云图
3 结语
论文对应力分类法、极限载荷法、弹塑性分析法进行了介绍,同时介绍了基于应变限制的评定方法。为压力容器的分析设计起了一定的指导作用。
