“数学分析”中各类积分对称性定理的统一性解释

艾正海，孙 峰

(乐山师范学院 数理学院，四川 乐山 614000)

0 引言

数学专业的“数学分析”[1-3]里涉及的各种积分的对称性是一个重要知识点，这类知识点是各类考试的考点和热点，合理利用对称性解题不仅会起到事半功倍的作用，而且也很有趣。同时，这些常见的积分类也是近现代数学的基础之一[4],虽然目前关于探讨各种积分的对称性文献[5-10]层出不穷，但这类文献往往仅介绍某一类积分的对称性，或者虽然介绍了各类积分的对称性，却开篇列出各种对称性定理，然后谈及应用。这类文献适合基础扎实的读者，但对于绝大多数读者而言，由于这些对称性定理众多又相似，使得读者难以记住和区分，特别地，第一类曲线(面)积分与第二类曲线(面)积分的奇偶性对称性容易混淆，再加上各种对称轮换性定理，就使得对称性更加复杂。当学生都难以记忆这些对称性定理的时候，应用也就更无从谈起了。

由于近二十年来大学的扩招，使得高校教育转变为大众教育，而不是精英教育，学生学习上缺乏自主性和主动性[11]，数学功底相比以前的学生也有了较大的距离[12]，在这种情形下，教学改革变得紧迫和势在必行[13]。另一方面，部分高校对“数学分析”的教学学时不得不进行压缩，在课时较少时[13]，如果我们单独对各类积分对称性进行详细探讨，学时也不允许。正如上文提及：这类知识点又是各类考试的考点和热点，特别地，一些想继续深造的同学经常问各种对称性的问题，鉴于此，如何对这些积分对称性进行精炼浓缩地讲解，又能让即使基础薄弱的学生也能很容易区分和记住这些对称性，是一个迫切要解决的问题。因此，本文对各种积分的对称性进行统一性探讨，以期有效地提高学生的学习能力。

1 定积分知识的简单回顾

为了更好地理解后续内容，定积分知识的简单回顾是必要的。

定理1 假设f(x)在[-a,a](a>0)为连续函数，则有

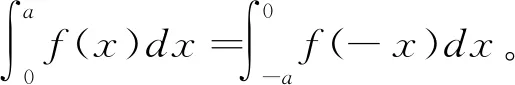
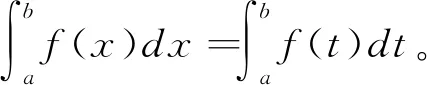
此定理说明定积分的值与积分变量无关。

2 重积分的对称性及应用

传统的对称性定理从关于x、y、(x,y)等的奇偶函数去描述，较为繁杂。本节从对称性和定义出发，给出这些二重积分对称性定理的简要解释和快速记忆方法。当把二重积分对称性搞清楚了，三重积分的对称性直接类推，非常容易地写出，因此本节不讨论三重积分的对称性。

定理3 设f(x,y)在有界闭区域D上连续，则有：

(a)设积分区域D关于y轴对称，则

其中D1=D∩{x≥0}；

(b)设积分区域D关于x轴对称，则

其中D2=D∩{y≥0}；

(c)设积分区域D关于原点对称((x,y)∈D⟺(-x,-y)∈D)，则

其中D3为D的右半平面或上半平面部分；

(d)设积分区域D关于直线y=x对称，即((x,y)∈D⟺(y,x)∈D)，则

∬D4f(x,y)dσ=∬D5f(x,y)dσ，

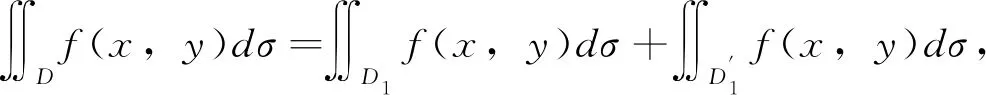
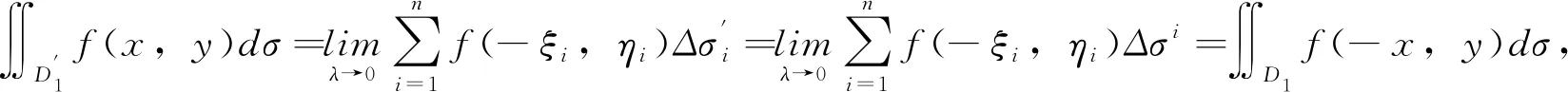
∬Df(x,y)dσ=∬D1f(x,y)dσ+∬D1f(-x,y)dσ，从而(a)结论成立。

记忆方法：首先，确定点(x,y)关于y轴对称的点明显为(-x,y)，再次，研究f(x,y)与f(-x,y)之间的关系：若f(x,y)=f(-x,y)，即不变号；若f(x,y)=-f(-x,y)，则变号。dσ为面积元，始终不变号。所以定理3可以记忆为：先找对称点，再看对应的二个函数之间是否变号(由于dσ为面积元，始终不变号)，变号为0，不变号为2倍。

以(c)为例：首先，(x,y)关于原点对称的点明显为(-x,-y)；再次，研究f(x,y)与f(-x,-y)之间关系；最后，若变号(即f(x,y)=-f(-x,-y))则为0，不变号则为2倍。利用这个方法，我们很容易写出积分区域D关于直线y=-x对称时的情形，请读者自行补充。

定理4 设f(x,y)在有界闭区域D上连续，若积分区域D关于x,y具有轮换对称性,则

∬Df(x,y)dσ=∬Df(y,x)dσ

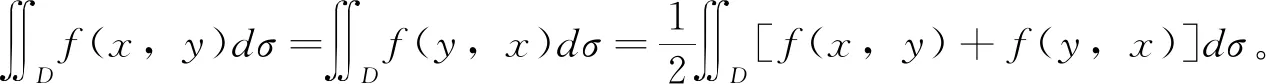
从上面的分析我们可以看出：对称轮换性的本质为二重积分的值与积分变量如何选取是无关的，这与我们之前提出的定积分的性质是类似的。下面通过例1、例2来说明在计算二重积分值时，如何利用对称性来有效地减少计算量。

例1 计算Ι=∬D(3x+2y)2dσ,其中D:x2+y2≤1。

解Ι=∬D(9x2+4y2+12xy)dσ，由于D关于x轴对称,而f1(x,y)=12xy=-f1(x,-y)，即变号了一次，故∬D12xydσ=0。由于区域D明显地关于x,y具有轮换对称性,因此，∬Dx2dσ=∬Dy2dσ。

进一步可得：

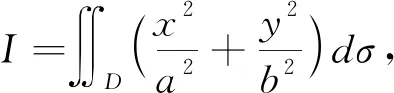
分析 因为D关于x,y具有轮换对称性，故可以运用定理4。

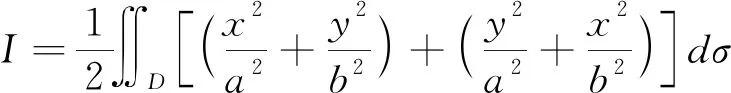
3 二类曲线积分的对称性与应用

由第一类曲线积分与第一类曲面积分的定义可知，二者的对称性是一致的；而第二类曲线积分与第二类曲面积分的定义仍然揭示了它们对称性也是一致的。因此，在本节我们仅仅讨论二类曲线积分的对称性与应用，这足以说清对称问题，对于曲面积分的对称性，读者可以直接类推得出。

首先，同上节一样，列出二类曲线积分的最核心的对称性定理。

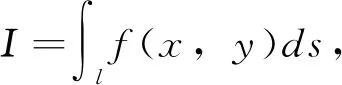
(a)若l是关于y轴对称,则

其中l1={(x,y)|(x,y)∈l,x≥0}；

(b)若l是关于x轴对称,则

其中l2={(x,y)|(x,y)∈l,y≥0}；

(c)若l是关于原点对称,则

其中l3={(x,y)|(x,y)∈l,x≥0,y≥0}；

(d)若l是关于y=x对称,则

其中l4={(x,y)|(x,y)∈l,x≥y}。

定理6 设L为平面上分段光滑的定向曲线，其中P(x,y)，Q(x,y)是连续的。则

(a)若曲线L是关于y轴对称，则有

其中L1是L右半平面部分。

(b)若曲线L是关于x轴对称，则有

其中L2是L位于x轴上方的部分。

对于第一类曲线积分的对称性(定理5)，仍然采取与二重积分对称性相同的分析法和记忆法，也容易看出二者的对称性结论类同，主要原因在于ds为长度的微元，仍然为正。对比定理5，定理6(第二类曲线积分的对称性)明显复杂于定理5(第一类曲线积分的对称性)。如果要求学生强行记忆，势必随时间推移定理结论易混淆。对此，我们仍然按照之前第二节中的介绍方法来处理，以(a)为例：

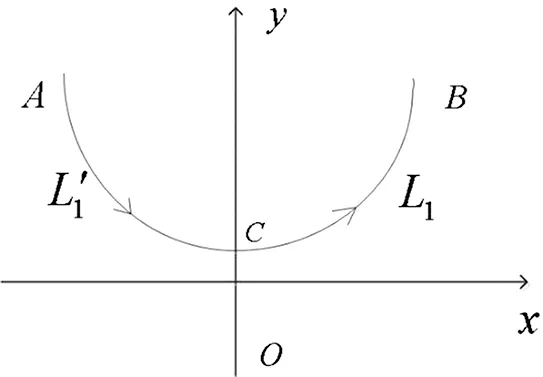
图1 定理6(a)示意

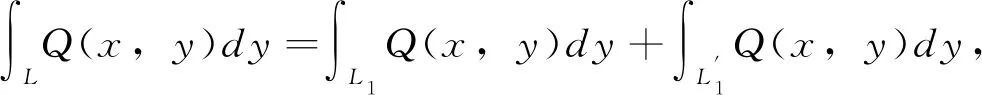
从上面的分析可以看出，对于第二类曲线积分，一方面考虑被积函数是否变号，另一方面考虑dx或dy是否变号，变了一次号为0，变了二次为2倍。关于原点对称、关于y=x对称，读者可按上述方法很容易给出，故在此不再列出。

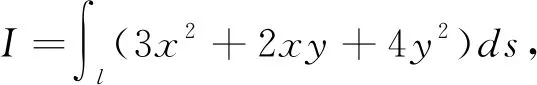
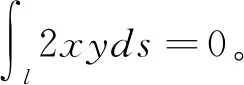
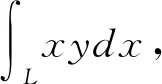
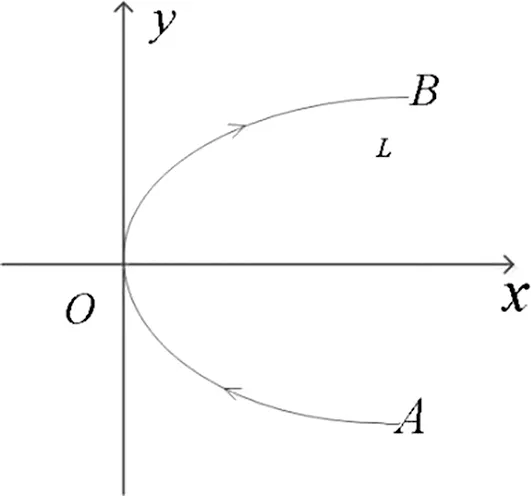
图2 曲线L

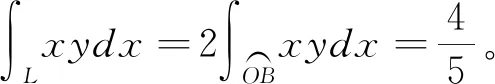
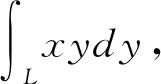
4 小结

本文讨论了各种积分的对称性，基本涵盖了数学专业“数学分析”里的各种积分；突破传统的各种积分对称性分别阐述的模式，也不再考虑各种繁杂的奇偶性，找出了这些积分关于对称性的共性，通过利用各种积分定义和类比定积分的手段，有效地解决了对各种积分对称性记不住和容易记混淆的问题。总体来说，各种积分对称性定理分四步走：一看积分区域(曲线、曲面)是否具有某种对称性，此为前提；二写对称点，看被积函数在此种对称性下是否发生了变号；三看微分在对称区域上(区间、曲线、曲面等)是否发生了变号；最后看被积函数与微分总共变了几次号，1次为0，2次为2倍。通过四步，无需再死记硬背各种积分的诸多对称性定理。此外，轮换对称性在多元积分里第一次出现，我们通过类比定积分，指出各种积分轮换对称性的本质为积分值与用什么积分变量无关，使其容易被理解。按照本文提出的方法，读者可以很轻松地写出当积分区域(区间、曲线、曲面等)关于y=-x对称和积分区域关于y=ax+b(a≠0)对称的相应对称性定理。总之，通过本文提出的四步走方法，各类积分的各类对称性定理变得清晰易记。