改进的虚拟力最大覆盖选址算法研究

汪浩祥，李 娜，李强懿

1.南京农业大学 工学院，南京 210031

2.南京航空航天大学 计算机与科技学院，南京 211106

1 引言

选址问题（CLP）一直都是供应链中十分重要的一环，配送中心的位置不仅关系到客户的服务水平高低还直接影响到整个配送过程的成本高低，所以一直以来都十分受学者们的重视。总的说来，目前选址模型的研究多集中在最大覆盖位置问题（MCLP）和集合覆盖位置问题（SCLP）。覆盖问题是传统选址模型的一个经典问题，最早是由Church和ReVelle[1]在1974年提出的，并被广泛应用于各个领域，尤其是针对公共设施比如医院、邮局、公园、学校的选址上有着许多应用。

Zarandi 等人[2]利用模拟退火算法对大规模动态覆盖选址进行了详细的求解，所提出的算法能满足2 500个节点和200个配送枢纽的服务需求，同时也填补了之前的研究对大规模动态覆盖问题关注不足的问题。Araz等人[3]提出了多目标的最大覆盖选址，考虑了基于覆盖的应急车辆定位模型的多目标模糊目标规划。最终的目标在于以更短的总运输距离来提高服务覆盖面积和服务水平。Erdemir 等人[4]提出了在节点和路径都产生需求情况下的最大覆盖问题，针对两种需求开发了两个不同的模型；针对节点的需求用通过基于模拟退火算法的贪婪算法对二次最大覆盖位置问题进行计算，针对路径的需求通过几何数学来进行计算；最后通过对移动手机用户和处于移动状态的手机用户的追踪数据确定了纽约州伊利县移动服务站的位置。Berman 等人[5]讨论了网络中存在负权情况下的最大覆盖问题，提出了该问题整数规划算法，并基于ILOG CPLEX 软件进行了算法实现；针对包含40个最大覆盖问题的数据集，分别采用上升算法和模拟退火算法这两种启发式算法进行求解与测试，最终表明模拟退火算法能够获得更好的结果。Alexandris 等人[6]通过对地理信息系统的使用和对部分覆盖思想的阐述对传统的覆盖模型进行了一定的扩展，得出相比较传统覆盖模型而言新模型对需求节点有了更大比例的覆盖。Corrêa等人[7]提出用列生成和覆盖图的方法解决最大概率覆盖问题，将图论引入到了覆盖问题中。

Church 和ReVelle[8]证明了最大覆盖问题在加入强制性覆盖范围的情况下可以等价于p中值问题，进而讨论了适用于p中值问题的方法也适用于最大覆盖问题，例如Maranzana[9]所提出的带权重的顶点中位数的启发式算法，在合理地选择初始值的情况下该算法可以得到很不错的结果，由于该算法是将服务点分配给最近的节点来服务，若同等距离则优先分配给更小的节点，所以在出现零权重时会出现算法无法收敛的情况。基于此Teitz 和Bart[10]提出了基于加权图广义顶点中位数估计的启发式方法，很好地解决了Maranzana算法不可收敛的问题，该算法通过遍历未被选定的潜在点，一旦该点产生更好的结果，则当前节点被替换，但遍历的结果导致该算法的复杂度极高。Chiyoshi等人[11]在Teitz和Bart的顶点替换方法的基础上结合了模拟退火算法，提出了应用于p中值问题的模拟退火的方法，该算法先通过模拟退火算法寻找出最适合的可能会用于交换的顶点，在该顶点产生更优结果的情况下进行替换，模拟退火算法的使用极大地提高了该算法的效率，但同时一个点也可能会存在被多次选中的情况，但与Teitz 和Bart 的算法相比，该算法的复杂度降低了50%以上。

Church 和ReVelle[8]提出的在最大覆盖选址加入强制的封闭性约束，将最大覆盖问题转化成p中值问题来求解，这一转化的确使得问题简化，但是p中值问题所围绕的解决目标都是最小化（路径，成本，时间）问题，这一求解特性使得该模型与最大覆盖问题有最原始的背反；同时在实际中存在更多的是非线性的情况，也就是说并非每一个最大覆盖选址模型都可以通过加入强制性范围约束转化成一个纯线性的p中值问题来求解。基于改进的虚拟力的配送中心选址算法以最大覆盖率为目标，以最终迭代的最大覆盖率节点所在位置为最优点，不用费力转化从所有潜在的优值中找到一个或者几个更优值；同时基于改进的虚拟力的配送中心选址算法考虑到了配送系统中每一个客户对节点及节点对节点之间的影响，将每一个可能的约束转化成力的影响也能更加直观地反映系统的即时状况。

国内对最大覆盖选址的研究在初期主要是对所用方法的分类和对国外学者的借鉴。乔联宝[12]在其2015年的综述里将覆盖选址问题分为确定性选址模型和概率选址模型两大类。其中确定性选址中包含了集合覆盖和最大覆盖问题，概率选址模型中又包括了概率集合覆盖模型、最大期望覆盖模型、最大可获得性覆盖模型。肖建华等人[13]提出了基于非等半径覆盖选址的膜计算方法来对生鲜农产品的配送中心进行选址。马云峰等人[14]考虑了基于时间满意度来进行的最大覆盖问题选址。刘慧等人[15]考虑了最低服务水平下的联合覆盖选址问题的选址效益。魏延青等人[16]根据受灾区域的受灾程度进行了分层，考虑到不同受灾区域的物品需求满意度和救灾预算成本等因素，并以救灾物资需求满意度为目标建立了最大问题覆盖选址模型，最后，通过实际数值实验，讨论了不同预算成本下和各受灾区域物资各不相同的满足标准对物资分配中心的数量和地址的影响。

从以上覆盖问题的发展方向来看，主要的解决方法几乎都是依靠着现代计算机而逐步发展起来的智能算法，同时前人对动态覆盖选址模型的理解并不完全是“动态”[17]。本文为了改善配送中心部署时的不合理分布，提高服务覆盖率，以配送中心覆盖率为优化目标，设计了一种将移动选址过程分为多个步骤的配送中心移动方案，通过不断比较各个配送中心之间所受虚拟力的大小，使配送中心逐渐移动到更合理的位置，以提高配送网络的覆盖率，与文献[18]所不同的是本文不需要考虑配送中心的总移动距离，模型中的移动对选址来说只是一个虚拟的过程，所要求的最短移动距离只是对移动过程的一个约束，并不存在任何成本，本文所关注的重点在于最终的移动结果。

本文将配送区域离散化成像素格子来进行配送中心的选址，在这一抽象平均化的条件下配送中心可以在所设置的条件进行移动，根据虚拟力配送中心在一次次的移动过程中逐渐到达更优的位置，最终所抵达的位置就是使得覆盖率最高的位置，也是最符合预期的选址位置。

2 问题描述与模型构建

2.1 问题描述

本文将整个需要服务的市场区域覆盖率Rarea定义为能被给定的配送中心所能经济服务到的（在其配送半径以内的称为经济服务，超出服务半径以外的则称为不经济配送）客户的面积Aarea和整个需要服务的市场区域总面积As之比，目标是最大化区域覆盖面积。为方便问题求解，假设：

（1）各个配送中心能够获取自身和所有其他配送中心的位置信息。

（2）配送中心位置移动过程中不考虑其他因素。

（3）配送中心有相同的服务半径Rd和通信半径Rc，其中通讯半径为全局覆盖半径。

（4）各个客户点pi的需求都是相同的。

2.2 模型构建

本文相关符号说明如下：

（1）Rd：配送中心的服务半径；

（2）Rc：配送中心的通信半径；

（3）Re：感知误差范围；

（4）Rarea：配送覆盖率；

（5）Aarea：被经济服务到的客户总面积；

（6）As：需要被服务的客户总面积；

（7）Pmin：最低感知概率，在单个配送中心P(pi,dj)≥Pmin时，则pi被服务到；

（8）λ：pi释放出的信息强度，信息越强则越容易被感知到，根据指数分布的特点和引力定律，λ的值越小则在距离越近的情况下越容易被感知到；

（9）β：配送中心的感知能力参数，本文根据万有引力定理将其取值为2；

（10）j：配送中心的编号，每个配送中心有唯一编号；

（11）i：客户的编号，每个客户也有唯一编号；

（12）Rd'：障碍物配送中心对其他配送中心的有效影响距离；

（13）pi：第i个客户；

（14）dj：第j个配送中心；

（15）d(di,dj)：配送中心di和dj之间的距离；

（16）Mdj：第j个配送中心的质量；

（17）F(pi,dj)：第i个客户对第j个配送中心的作用力；

（18）di'：第i个障碍物配送中心；

（19）α：配送中心的作用能力参数，本文根据万有引力定理将其定为2；

（20）Fmin：虚拟力的最小起作用值；

（21）Maxstep：是配送中心dj所允许的最大移动距离；

（22）Nj：配送中心dj的邻居列表；

（23）m：循环次数。

为建立本文数学模型，首先给出如下定义：

定义1第i个客户pi被第j个配送中心dj所服务到的概率定义为P(pi,dj)，即：

其中，d(pi,dj)是第i个客户与第j个配送中心dj之间的距离，Rd是该配送中心的服务范围。

客户点pi被所有的配送中心服务的概率为：

根据上述定义，假设二维平面配送区域内有A×B个客户，每个客户面积大小表示为Δx×Δy，第i个客户点可以被配送网络服务的概率为P(pi)，当P(pi,dj)≤Pmin时，P(pi)=0，则该客户点未被配送网络中的任一个配送中心所服务到；当P(pi,dj)≥Pmin时，P(pi)=1，该客户点可视为被配送网络所服务。第i个客户点pi是否被配送网络的配送中心所服务到用Pcov(pi)来衡量，即：

根据上述定义，建立本文数学模型如式（4）所示：

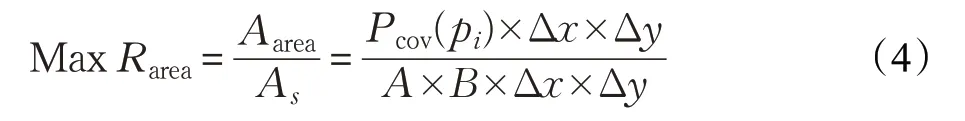
目标为最大化区域覆盖率Rarea。

3 改进的虚拟力算法

基于改进的虚拟力的最大覆盖选址模型受启发于物理学中的带电微粒，带电粒子之间互相存在引力和斥力，这一理论在无线传感器放置领域已经有了很多的应用[19]。假设服务区域为电场，配送中心为电场中的带电粒子，这样配送中心之间存在相互作用的力，在这些力的作用下使得配送中心尽可能地分布合理提高配送中心对所服务区域的覆盖效果。基于改进的虚拟力的选址模型中，如果两个配送中心之间距离较远则引力起到主要作用，如果距离过近则斥力起到主要作用。同时，如果存在障碍物，则该障碍物对其起到斥力作用，服务区的边界对配送中心既起到引力作用又起到斥力作用，这样可以避免服务区域边界出现较大的覆盖漏洞。

3.1 配送中心移动方案

在整个服务范围区域内随机分配N个配送中心，用dj代表配送中心网络中的第j个配送中心，则配送中心节点集合为D={d1,d2,…,dj,…,dN}。

改进的虚拟力算法是将配送网络假设为一个包含力、加速度和质量的虚拟物理系统，配送中心、障碍物和服务区域均可以对配送中心产生引力或斥力，配送中心移动的方向和距离取决于该配送中心自身的位置，以及所受相邻配送中心节点的引力与斥力的合力，配送中心节点需要移动到受力平衡的位置。

（1）配送中心受相邻配送中心节点间的斥力

任意两个配送中心节点di和dj，则配送中心di受到配送中心节点dj的斥力可表示为：

配送中心之间的距离过远时，引力不起作用；距离过近时，两个配送中心不可能同时锚定在同一个位置，所以在配送中心之间的作用力只考虑斥力。

（2）配送中心受到客户pi引力

配送中心节点dj受到来自客户pi的引力作用，引力可表示为：

每一个客户都要尽可能地“吸引”更多的配送中心来服务他，不存在要把配送中心推到一边的做法，所以客户和配送中心之间只存在引力这一种作用力。

（3）配送中心受到来自障碍物的斥力

为防止配送中心在移动过程中碰到不可锚定的位置，在不可锚定的位置设置障碍物，为了保证系统的连续性，将障碍物设置为具有固定位置的配送中心，这些配送中心对其他的配送中心只产生斥力，使其他配送中心不会移动到该障碍配送中心的位置。则配送中心dj受到障碍配送中心di'的斥力可表示为：

（4）配送中心所受到的合力

对任意的配送中心dj，将客户、配送中心节点和障碍物对配送中心的作用力分别建立二维坐标轴进行分解，则配送中心dj受到作用力可以表示为：

沿X轴的合力：

沿Y轴的合力：

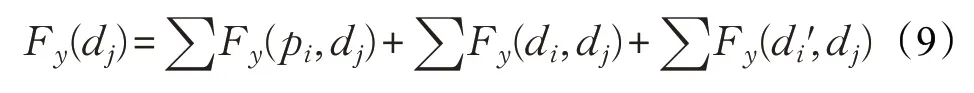
受到的合力：

为了降低算法的复杂度，在本文中不设置障碍物，假设整个服务区都可以作为配送中心锚定的地点，同时因为配送中心与配送中心之间的斥力存在是为了任意两个配送中心锚定的地点不重合，在移动过程中这个问题不会发生，加上两个质量相同的物体所产生的斥力在整个系统中是趋于平衡的，所以式（8）和（9）中的后两项作用力对配送中心的移动过程影响很小，可以忽略不计。

（5）配送中心的移动方案

通过计算以配送中心节点dj为圆心，Rd为服务半径的圆形区域内的客户pi被感知的概率，决定配送中心dj的移动，配送中心会不断地朝着感知概率低的地方移动，同时感知概率低的地方也是配送中心节点比较稀疏的地点。如果配送中心dj所受的虚拟力小于最小起作用值，则不需要移动。

配送中心dj经过受力计算后，根据所受合力的大小将配送中心节点从原位置(xj,yj)移动到新位置(xj',yj')。

在整个移动过程中，配送中心的位置可能会超出所规定的服务范围边界，这样明显是不合理的。如果在一次移动中，新的位置位于服务范围的外部，则这一次移动不再进行，也就是该配送中心的位置坐标同上一次的移动结果保持一致。

3.2 算法步骤

步骤1对服务区中的每一个配送中心所释放出的信息进行检测，读取每个配送中心的编号和位置信息，进入步骤2。

步骤2如果配送中心dj收到邻居节点所发出的信息，更新其邻居列表Nj的信息，进入步骤3。

步骤3通过定义1 中的公式计算出配送中心dj周围半径为Rd+Re的圆形区域中客户pi的被感知的概率P(pi)，进入步骤4。

步骤4通过公式（5）～（12）计算出配送中心dj需要移动到的新位置(xj',yj')，如果需要移动到的位置位于服务区域的外侧，则该次移动不发生，进入步骤5，否则移动到新位置再进入步骤5。

步骤5如果达到设置的算法循环次数则算法退出，否则转向步骤1，进行新的循环过程。

4 仿真结果及分析

使用Matlab软件对该算法进行仿真，假设在300 km×300 km 的服务区域A 中随机确定N个配送中心，配送中心的服务半径Rd=60 km,β=2,λ=0.2,α=2，通信半径300 km，感知误差范围Re=1 km，移动过程m=200次，最低感知概Pmin=0.9，最低感知概率越低则客户被服务到的概率越大，同时被重复服务的概率也越大，但是服务的稳定性不够，且所需要的配送中心数量也会更多些，在实验过后选择在Pmin=0.9 的感知概率下更符合实际情况。随机放置的配送中心的覆盖率是在5 000次模拟之后取得的平均值。为了防止配送中心移出服务区域A，如果配送中心的新位置移动到服务区域A内部20 km 宽的边缘区域时，配送中心节点将不会移动，仍处于原位置。

令N=5，6，7，8，9，10，11，12，13，14，15，分别采用随机部署和本文基于改进虚拟力算法进行仿真，两种部署算法的覆盖率如表1所示。

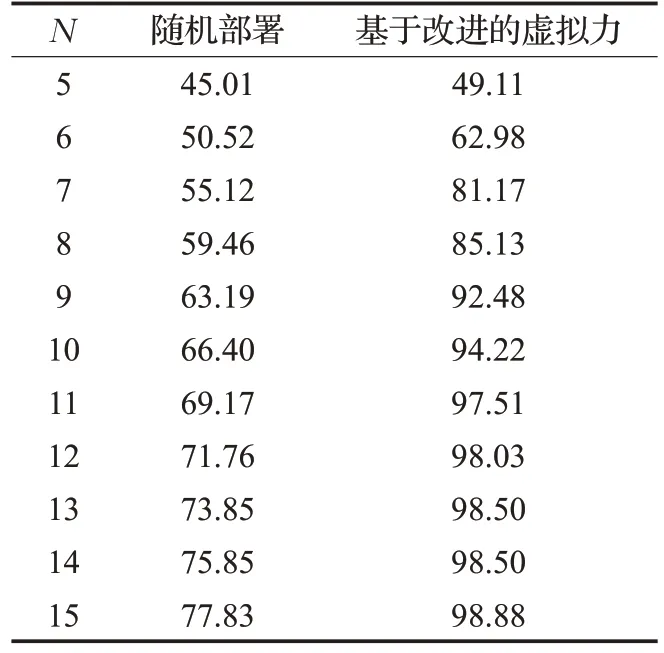
表1 两种部署方法的覆盖率 %

图1 到图8 为算法仿真的部分结果，每张图中的圈代表每个配送中心的覆盖范围，圆心代表配送中心最后锚定的位置。

图1 当N=5 时基于改进的虚拟力算法

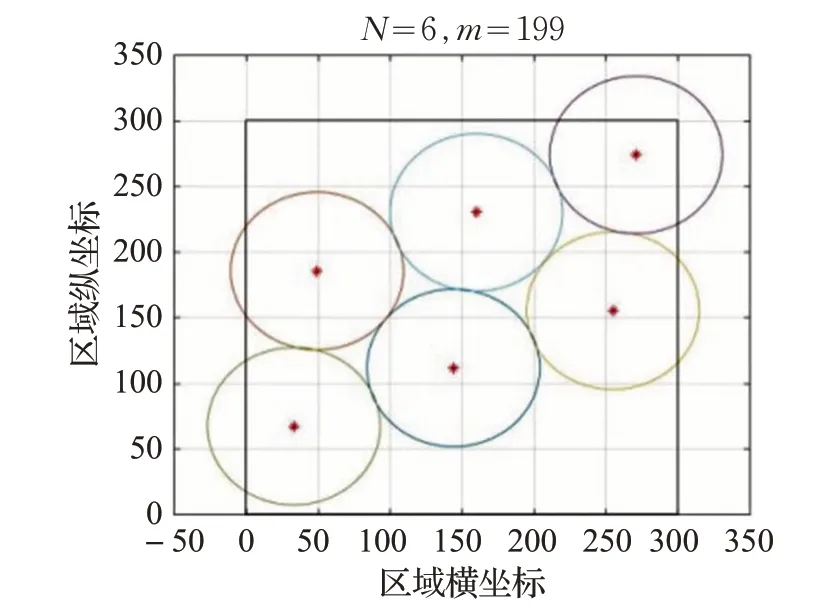
图2 当N=6 时基于改进的虚拟力算法

图3 当N=7 时基于改进的虚拟力算法

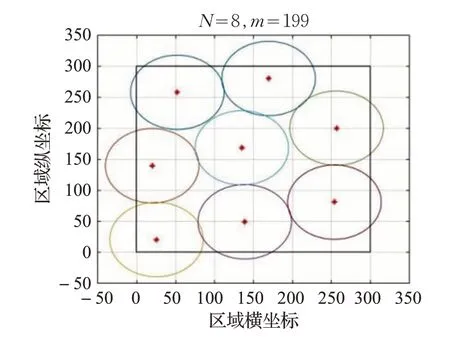
图4 当N=8 时基于改进的虚拟力算法

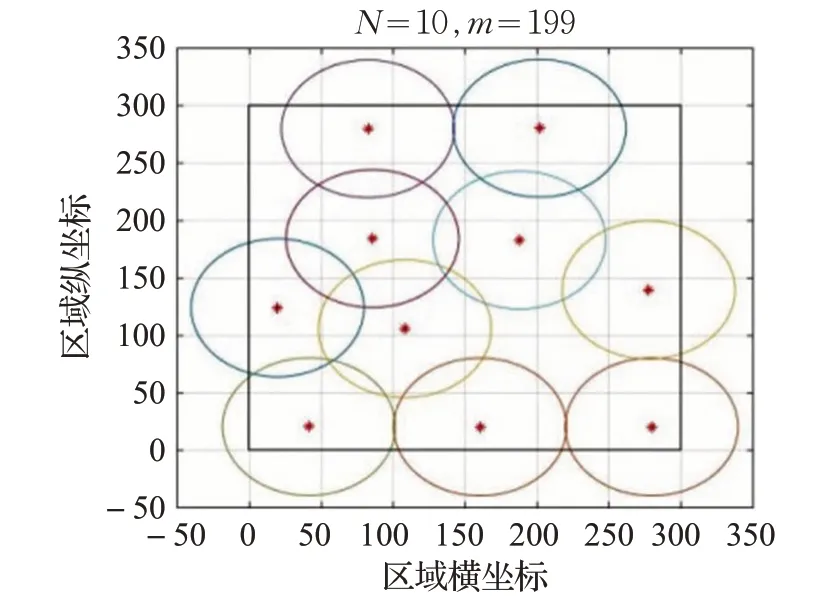
图5 当N=10 时基于改进的虚拟力算法

图6 当N=12 时基于改进的虚拟力算法

图7 当N=14 时基于改进的虚拟力算法

两种部署方法覆盖率比较如图9所示。

仿真结果表明，基于改进的虚拟力算法让覆盖率平均提升了22.58%，这意味着可以用更少的配送中心来服务更多的客户，极大地降低了配送的成本。从图1到图8 可以看出在N=10 之后配送中心覆盖范围的重合度越来越高，配送中心的利用效率逐渐降低。同时，从表1与图9可以看出，当N大于12以后，覆盖率提升的边际效应就逐渐接近于0 了，出于经济考虑，选择更少的配送中心来完成工作显然会更为合理。

图8 当N=15 时基于改进的虚拟力算法

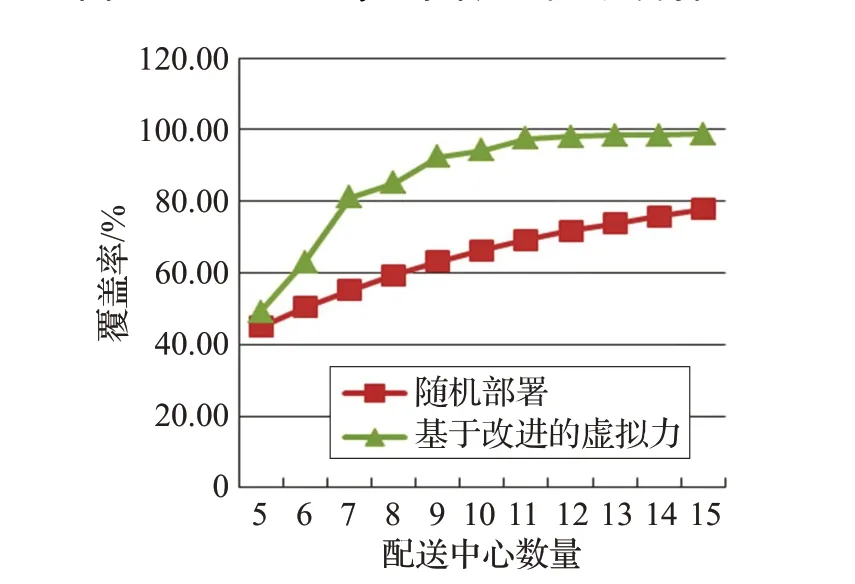
图9 两种算法结果的比较

5 总结

基于改进的虚拟力的配送中心选址算法根据配送中心节点周围区域的被感知概率进行移动，使配送中心节点向感知概率低的区域移动，在配送中心节点密集处也能实现理想的效果，使配送中心逐渐移动到最佳的监测位置，在提高覆盖率的同时减少了每个配送中心移动的距离，使配送中心移动距离的总和较小，也就使得仿真所需的时间相对较少；同时基于改进的虚拟力的覆盖选址模型可以支持异构的配送中心，也更符合实际的生产情况。

在未来的研究中可以尝试从客户的地理分布随机，客户需求情况随机入手进行单个或者组合考虑；还可以考虑配送中心异构的问题（给配送中心分类），在异构的条件下根据配送中心的能力来确定其配送半径，再结合客户需求随机的情况使得该问题在覆盖方面的研究更加贴近现实情况。