几类特殊的多面体的外接球问题
2020-10-19沈清臣
沈清臣
(湖南省长沙市长郡中学 410000)
空间几何体与球的组合问题是近几年高考中的一个频考点,且考查形式灵活多样;要正确求解此类问题,学生必须通过读、想、画、转、算五个基本环节,找准熟悉的基本几何模型及相应的求解策略.
此类问题可划分为旋转体、多面体的内切、外接球问题;而旋转体的内切、外接球问题,通过轴截面可转化为平面几何问题求解;多面体的内切球问题,利用等体法可直接求解.因此,本文主要介绍多面体(棱柱、棱锥)的外接球问题,在此之前,我们先熟悉空间球体的截面性质及其应用.
一、球的截面性质及其应用
如图1,空间球体有如下性质:
(1)用一个平面去截球,所得截面是一个圆面;
(2)球心与截面圆心的连线与截面垂直,且满足:R2=r2+d2(其中R表示球的半径,r表示截面圆的半径,d表示球心到截面的距离).
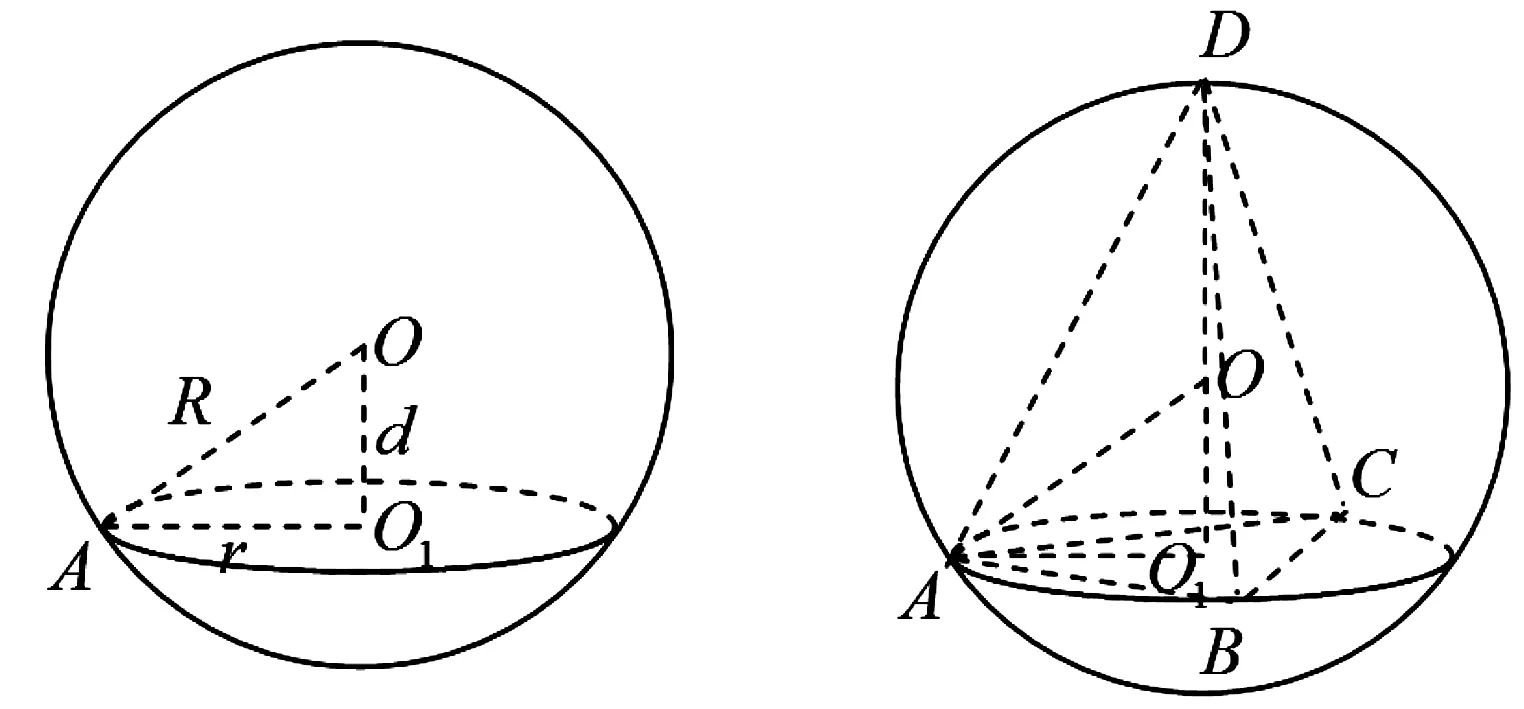
图1 图2


上例的求解过程,充分利用球体的截面性质,即球心与截面圆圆心的连线与截面垂直,使得求解难度大大降低.类似的问题还在高考试题中曾多次出现,如2013年新课标Ⅰ(理)第6题、2013年新课标Ⅰ卷(文)第15题、2013年大纲卷(文)第16题、2013年大纲卷(理)第16题等.其实,更多几何体的外接球问题的求解均需要利用到球体的截面性质,在后面的问题中将作介绍.
二、棱柱的外接球问题
此处我们主要介绍直棱柱(侧棱垂直于底面)的外接球问题.因为正方体、长方体的外接球直径即为体对角线,因此遇到直棱柱的外接球问题,首先可以考虑将该直棱柱补体为长方体或正方体;若不能补体,再考虑利用球体的截面性质确定球心位置,再由勾股定理求解.
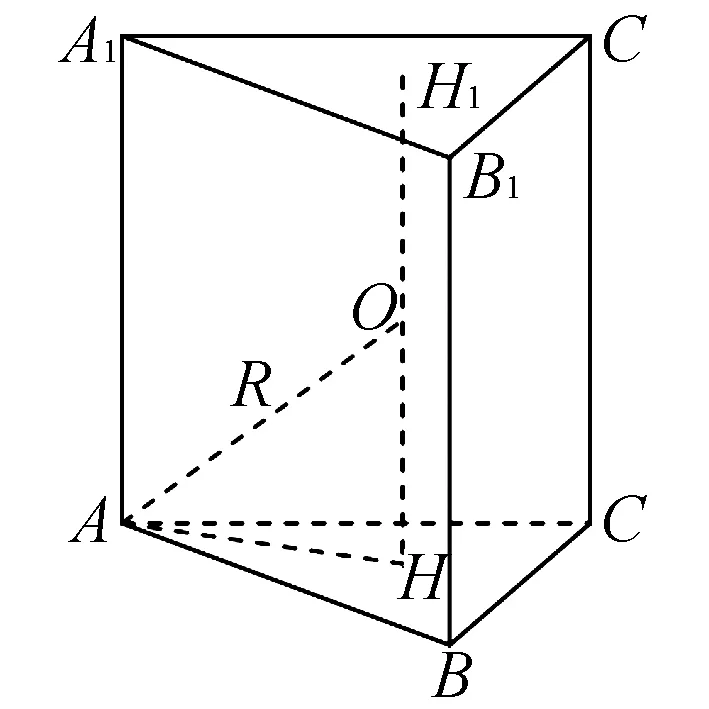
图3
如图3,设直三棱柱ABC-A1B1C1上、下底面的外接圆圆心分别为H1、H,连接H、H1,则易知HH1的中点O即为该棱柱外接球的球心,AH即为底面外接圆的半径,AO即为球的半径R.利用平面几何知识求出AH,再结合球的截面性质可直接求解.
例2(2013年辽宁文、理第10题)已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( ).


直接考查正方体、长方体的外接球问题,在高考试题中曾多次出现,如2013年天津文第10题、2014年陕西理第5题、2016全国Ⅱ文第4题、2017年天津文、理第10题、2017年全国Ⅱ文第15题等,此类问题难度不大.
补体的策略在后面的锥体的外接球问题中将进一步详细介绍.
三、棱锥的外接球问题
球与锥体的组合问题,在高考真题及各地的模拟试题中出现频率最高,试题形式多样,灵活多变.类似于柱体的求解策略,我们首先考虑补体,再者利用截面性质确定球心,进而可得解.下面将按四种类型进行详细阐述.
1.有条侧棱垂直于底面的棱锥
若棱锥的一条侧棱垂直于底,则补体为直棱柱求解,如图4,三棱锥S-ABC中,侧棱SA⊥底面ABC,则可补体成直棱柱SQP-ABC(如图5),即转化为直棱柱的外接球问题.

图4 图5
例3(2019年全国Ⅰ理第10题)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( ).


图6 图7
在三棱锥中,若共顶点的三条棱两两垂直,则将棱锥补体为正方体或长方体,可迅速求解.类似问题再如,2012年辽宁文理第16题.
2.对棱相等的锥体
正方体或长方体中,相对面的对角线相等,因此当三棱锥的对棱相等的时候,可以将该三棱锥放于正方体或长方体内,即补体为正方体或长方体.


图8

∴球的半径R满足4R2=a2+b2+c2=7,故表面积为S=4πR2=7π.
本例也可以取AB或CD的中点,作出截面,根据几何体的对称特征,确定球心的位置,利用球的截面性质列出方程组求解.但两种解法对比,可体现上述解法的简便快捷.特别是准确熟悉正四面体与正方体之间的联系,可快速解决正四面体的外接球问题,比如下面的例题.
3.正棱锥(底面为正三角形,顶点在底面的射影为底面的中心)

图9
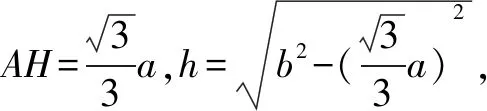
例5(2014年大纲文第10题、理第8题)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( ).

图10
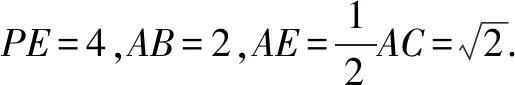
上述例题的求解过程,还是利用球体的截面性质.前述例3(2019年全国Ⅰ理第10题)亦可利用上述方法求解.
4.有两个面垂直的棱锥
如图11,已知球O1、O2的两个截面圆所在平面垂直,则四边形OO1HO2为矩形,且△OAO1,△OBO2均为Rt△,AO=BO=R.利用勾股定理结合已知条件列出方程组,即可求解.
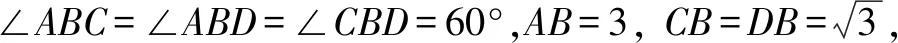

图11 图12


设△BCD,△ACD的外接圆圆心分别为E、H,四面体A-BCD的外接球球心为O,则OE⊥平面BCD,OH⊥平面ACD,OEFH为矩形,∴OE=HF,OH=EF.
连接AO、BO,并设外接球半径为R,OE=HF=x,则分别在Rt△BOE,Rt△AOH中可得:
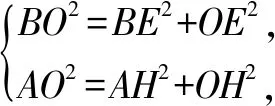

上述例题的求解过程,还是利用球的截面性质(过截面圆圆心且与截面垂直的直线一定过球心),通过两个截面来确定球心的位置,再利用勾股定理求解.
其实,一般情况下,并要求两个截面圆所在平面垂直.如下例:
例7(2020年广州市一模文 第12题)在三棱锥A-BCD中,△ABD和△CBD均为边长为2的等边三角形,且二面角A-BD-C的平面角为120°,则此三棱锥的外接球的表面为( ).

图13


以上内容是对常见的棱柱、棱锥的几类外接球问题及其求解策略的归纳.因为题型可以灵活多变,问题的求解途径多种多样,以上肯定有阐述不全面不到位的地方,期盼读者去补充完善.
