隐匿的均值不等式

梁宗明

(甘肃省兰州市兰化一中 730060)

均值不等式是高中数学中求解、求最值的重要工具，也是历年的高考热点，许多问题均值不等式的条件非常明显，但是也有很多问题，均值不等式的属性隐匿得比较深，需要我们拓展思路，巧妙转化，挖掘均值不等式的属性巧解一些问题.

一、重要不等式

∀a,b∈R,有a2+b2≥2ab，当且仅当a=b时，等号成立；

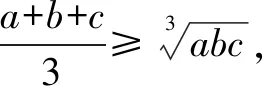
二、应用举例

例1 设x,y为正数，且x4+4y4+1=2x2y2+2y2+x2，求x,y的值.

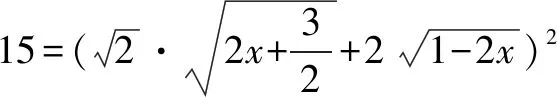
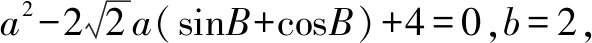
例6(2015北京卷)设{an}是等差数列，则下列结论正确的是( ).

A.若a1+a2>0,则a2+a3>0

B.若a1+a3>0，则a1+a2<0

D.若a1<0,则(a2-a1)(a2-a3)>0

A．13 B．15 C．19 D．21

图1

图2

解析依据∠ABC=60°,因此以B为坐标原点建立如图直角坐标系.