基于生物地理学算法的水电机组PID参数优化

高 菘，杨 虎，付恩狄，刘 冬，黄一冲，肖志怀

(1.天生桥二级水力发电有限公司，广州 510000；2.武汉大学动力与机械学院，武汉 430072；3.中车株洲电机有限公司，湖南 株洲 412000)

在水电机组运行中，工况点的偏移会导致水轮机的流量和力矩特性参数发生变化。由于控制对象的不断变化，水电机组时刻存在调速系统的控制效果变差，稳定性变差的危险。随着现代水轮机朝着大容量、高水头、高比转速的方向发展，对调速器调节性能的要求也随着用电部门对电能质量的要求而不断增加。水电机组的优化控制主要针两方面：一是提出新的控制策略；二是对现有参数进行优化。

PID控制理论在一定程度上无法满水轮机调速系统的非线性、变结构、变参数等特点，许多学者提出了不同于PID控制的新控制理论[1-3]。王淑青设计了基于非线性自回归动态神经网络(NNARX)的水电机组预测控制系统，该方法控制精度高，适于水电机组难以用数学模型表达的物理过程[4]。王斌在研究李雅普诺夫稳定性和有限时间控制的基础上，提出了一种基于终端滑模面的水轮机控制器[5]。孔繁镍设计的水轮机鲁棒控制系统，比传统PID控制有更优秀的时域性能[6]。

但新型控制策略的研究只停留在理论阶段，水电站使用的调速器依旧使用PID控制策略，其参数的整定具有经验性，往往根据厂家给定或是电厂手动整定，因此PID控制参数的整定需要更准确有效的手段。对于水轮机运行过程中工况点发生变化，导致一组固定PID参数无法满足控制要求的问题，可采用自适应算法如模糊系统实时调整PID参数[7-9]。曹程杰根据变参数PID的思想提出了适应式控制规律，针对水轮机运行工况点参数，采用智能算法求取当前最优PID参数[10]；王华强给出了一种基于模糊PID的水轮机调速系统，在一定运行工况范围内，利用模糊数学集整定当前工况下PID的具体参数[11]；郭爱文将遗传算法与神经网络结合，提出了基于遗传神经网络的水轮机调速器自整定PID控制[12]。针对一组PID参数控制效果不佳，整定困难的问题，可通过人工智能如启发式算法对参数进行寻优[13-15]。寇攀高使用菌群-粒子群算法对水轮机调速器PID参数进行优化[16]；李超顺设计了一种基于万有引力算法的非线性水轮机调速器PID控制系统[17]；付文秀则利用果蝇算法优化水电机组PID参数[18]。

本文针对SK电站功率模式下的机组优化控制问题，建立了相应的分段线性模型，在此基础上，基于生物地理学优化算法，对某工况的PID控制参数进行了优化，并通过仿真和对比试验验证了新方法的可靠性和精度。

1 水电机组基本模型

水轮机调节系统主要包括调速器、水轮机及引水系统、发电机及负载等构成的闭环控制系统。当控制系统受到扰动时，调速器根据给定量和反馈量的差值控制随动系统做出动作，使反馈量与给定量的差值逐渐趋于0，达到新的稳定状态。在水电机组功率控制模式中，反馈信号取自机组功率。本节主要介绍水电机组各个子系统在功率模式下的建模方法，搭建水电机组整体线性模型。

1.1 引水系统模型

若在扰动较小的工况，且当管道长度较短时，可以忽略引水管道中水流和管道壁的弹性，采用常见的刚性水击模型，如式(1)所示：

(1)

式中：Tw为水流惯性时间常数。

刚性水击模型是水轮机调节系统建模中常用到的模型，一般认为，在小波动情况下，满足压力管道长度小于600～800 m的条件时，该模型亦能够满足建模要求。根据SK电站输水系统结构，其等效引水管道长度小于300 m，故使用刚性水击模型。

1.2 发电机—负载模型

对于水轮机调节系统来讲，发电机-负载一阶模型足以满足动态特性研究，发电机的简单一阶模型中只有转动惯性量，根据动力学原理，列出刚性旋转体运动方程：

(2)

式中：J代表转动部分的转动惯量；w代表转动部分的角速度；Mt为水轮机主动力矩；Mg代表总阻力矩。在工作点附近线性化并取标幺值，得：

(3)

式中：eg为阻力矩对转速的偏导数，又被称作发电机自调节系数，其值的大小取决于电网，一般取为0.4～2.0之间；Ta表示机组惯性时间常数。

1.3 调速器模型

本文针对SK电站建立功率控制模式下的PI型控制器模型，其结构如图1所示，包含限速环节和PI控制逻辑两个部分。

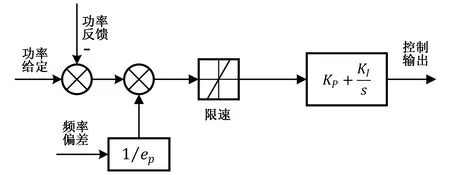
图1 SK电站控制器模型Fig.1 Controller model of SK power station

随动系统与控制器共同构成调速器，可将控制器的输出控制信号转化为相应的机械信号，调节导叶动作。对于常用电液随动系统，在不考虑高阶项、非线性因素和延迟环节的情况下，线性随动系统传递函数如式(4)所示：

(4)

式中：YG为随动系统输入，即控制器的输出信号；Y为接力器的位置，即随动系统输出；Ty为接力器时间常数。

1.4 水轮机模型

水轮机有复杂的非线性特点，运行时影响流场的因素复杂，存在很多不确定性，目前只能依靠模型综合特性曲线和飞逸特性曲线的方法来描述水轮机特性。在水轮机工况缓慢变化时，可近似用稳态特性来描述动态特性，即在小扰动情况下，可使用线性模型来近似描述，如式(5)和(6)。

q=eqxx+eqyy+eqhh

(5)

mt=exx+eyy+ehh

(6)

式中：q为水轮机流量；mt为水轮机力矩，eqx、eqy、eqh为与流量有关的传递系数；ex、ey、eh为与力矩有关的传递系数。

1.5 系统整体模型

根据以上子系统模型，搭建SK电站水轮机调节系统分段线性化整体模型，水轮机模型采用基于传递系数的线性模型，调速器采用并联PI控制，引水系统使用刚性水击模型，发电机采用一阶简化模型，整个系统采用功率控制模式，控制反馈由功率引入，模拟接入大电网运行，故并网后转速不变，因此忽略力矩和流量对转速的传递系数ex和eqx。系统的分段线性化模型如图2所示。

图2 SK电站功率模式下水轮机分段线性化模型Fig.2 Segmental linearization model of hydraulic turbine under power mode of SK power station

2 生物地理学算法

BBO算法的核心是迁移和变异，是其交换信息的方法，迁移和变异使得栖息地间的物种信息相互流通，以此来改善栖息地的适宜度指数(HSI)值，通过一定概率的变异，模拟自然环境中的自然灾害事件和物种突变情况[19]。

2.1 迁 移

栖息地的HSI指数在栖息地物种发生迁移时也会被影响，迁入率和迁出率被外来物种所改变，迁入率λs和迁出率μs对物种数量的变化关系可用迁移率模型来表示，如图3。

图3 BBO算法的各种迁移模型Fig.3 Various migration models of BBO algorithm

(1)线性迁移模型。迁移率与生物种群数量成一次函数关系，当栖息地生物种类增加的时候，迁入率和迁出率的上升下降曲线类似一次函数，迁出率和迁入率与生物种群数量关系如下式示：

(7)

式中：S和Smax分别为栖息地当前物种数和最大物种数；I和E分别为迁入率和迁出率的最大值。

(2)指数迁移模型。迁移率与生物种群数量成指数关系，当栖息地生物种群数量变化时，迁移率曲线类似于指数函数，迁入率和迁出率与生物种群数量的关系如下：

(8)

(3)二次迁移模型。当栖息地生物种群数量变化时，迁移率曲线类似于二次函数，同时与指数迁移模型类似，迁入率和迁出率与生物种群数量的关系式如下：

(9)

(4)余弦迁移模型。当栖息地生物种群数量变化时，迁移率曲线类似于余弦函数，如下式所示：

(10)

生物地理学算法的信息交换是根据生物种群的迁移来实现的，一个栖息地的迁移与否是根据设定的概率来判断的，如果要迁移，则选择一个栖息地为要迁入的栖息地提供特征分量，同时这个需要迁出的栖息地则根据其迁出率来进行选择，用需要迁出的栖息地的特征分量代替需要迁入的栖息地的特征分量，从而完成迁移操作。算法的具体实现方法如下：

(1)参数初始化，令i=1；

(2)以概率λi确定是否迁入到第i个栖息地；

(3)若确定迁入，则j=1，进入步骤(4)。否则，进入步骤(7)；

(4)以概率μj确定是否第j个栖息地是否迁出；

(5)若确定迁出，则从第j个栖息地随机选择一个特征分量，替代第i个栖息地中一个随机选择的特征分量。否则，进入步骤(6)；

(6)若遍历了所有栖息地，则进入步骤(7)。否则j=j+1，返回步骤(4)；

(7)若遍历了所有栖息地，则结束变异操作。否则i=i+1，返回步骤(2)。

另外，不同的栖息地物种迁移模型对算法的性能有一定的影响，接近自然规律的迁移模型比简化线性模型效果好，经过测试，余弦模型的性能在大部分情况下优于其他模型[20]。

2.2 变 异

BBO算法用变异操作来模拟自然界中环境突发性灾难事件。如火山喷发，彗星撞地球和传染病等会改变栖息地环境，同时适宜度指数HSI也因为这些灾难的发生而突然改变。生物发生变异的概率显然与物种的数量有关系，若种群数量较少，则发生变异的个体相对稀少，反之变异的概率则会较大，变异操作流程如下：

(1)参数初始化，令i=1，j=1；

(2)以概率Pi确定第i个栖息地的第j个特征分量是否进行变异；

(3)若进行变异，则用随机产生的特征分量xik代替原特征分量xij。否则，进入(4)；

(4)若当前栖息地的所有特征分量得到遍历，进入步骤(5)。否则，j=j+1，返回步骤(2)；

(5)若所有栖息地得到遍历，则结束迁移操作。否则，i=i+1，返回步骤(2)。

2.3 BBO算法流程

对于一个确定的优化问题，以HSI值作为评价函数，通过迭代进行变异和迁移操作，使HSI值不断优化，从而求得问题的最优解。生物地理学算法的步骤如下(如图4所示)：

(1)设置BBO算法的初始值(种群数量、问题维数、迭代次数、最大变异概率、精英保存个数等)；

(2)随机生成栖息地特征向量；

(3)对每个栖息地的适宜度指数HSI进行计算并排序，同时计算迁入率和迁出率；

(4)对栖息地进行迁移操作；

(5)保留精英种群，进行变异操作，同时重新计算所有栖息地HSI，再重新进行排序；

(6)如迭代满足要求，停止算法，不满足则返回步骤(3)。

图4 BBO算法流程图Fig.4 Flow diagram of BBO algorithm

3 基于BBO的PID参数优化

3.1 评价函数

对于水轮机调节系统，其控制品质的好坏可以从系统输出响应的超调量、上升时间、调节时间和稳态误差等方面来描述。时间与误差平方积分ITSE是常用的评价指标，表示时间乘以控制偏差的平方的积分。其值越小，说明误差在瞬态响应后期越小。本文使用该指标作为对PID参数进行优化的评价函数，其计算方法如下。

(11)

3.2 水电机组PID参数优化

水电机组功率调节模式下的PID参数优化过程如图5所示，由于某一确定工况下的水轮机模型传递系数是已知的，设置好算法的参数后，在Matlab/Simulink平台上进行模型仿真得到模型的输出，用输出值计算相应的评价函数，多次仿真反复迭代直到满足循环次数，最后输出寻优结果。

图5 PID参数寻优过程Fig.5 Optimization process of PID parameters

4 优化实例对比

为证明BBO算法的性能，与遗传算法进行比较设计参数优化实验，使用图2所示的整体线性模型进行负荷扰动试验，选择SK电站水轮机额定工况下的机组传递系数，如表1。

表1 SK电站额定工况的水轮机传递系数Tab.1 Transfer coefficients of hydro-turbine under rated operating condition

生物地理学优化算法参数设置为：迁移模型选择余弦模型，设置变异概率为0.1，最大迁入概率1.2，最大迁出概率为1；遗传算法参数：交叉概率为0.8，变异概率0.2。在功率模式下进行功率扰动试验，取5次运行的最优值，比较两种算法在不同迭代次数和种群数量时的优化结果。

(1)种群数量为50，迭代次数为30。如表2和图6所示，当种群数量为50 ，最大迭代次数为30次时，GA和BBO算法的ITAE指标均好于电站预设的Kp和Ki参数，分别为0.169 6和0.109 6，BBO的ITAE值最小。从图中可以看出GA优化后参数的响应曲线上升较平滑，但上升时间短，BBO上升时间长，调节时间短，电站预设参数与GA以及BBO优化后参数的超调量相差不大。

图6 1%功率扰动响应Fig.6 Time response of 1% power disturbance

表2 优化的参数及指标Tab.2 Optimal parameters and corresponding indicators

(2)种群数量为80，迭代次数为50。从表3和图7可以看出，当种群数量增加到80时，GA和BBO的ITAE指标进一步减小，分别为0.104 8和0.098 2，BBO的ITAE值最小。BBO优化后的调节时间最快，且无超调，GA的上升时间和调节时间均有所改善，但仍有超调，电站预设值的上升时间虽然短，但振荡次数最多，导致调节时间较长。

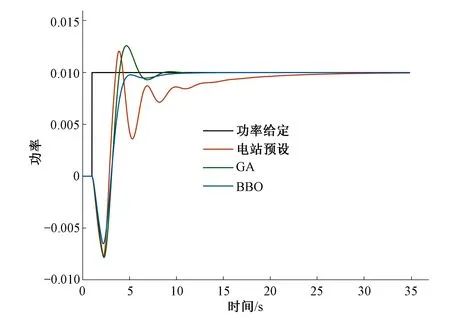
图7 1%功率扰动响应Fig.7 Time response of 1% power disturbance

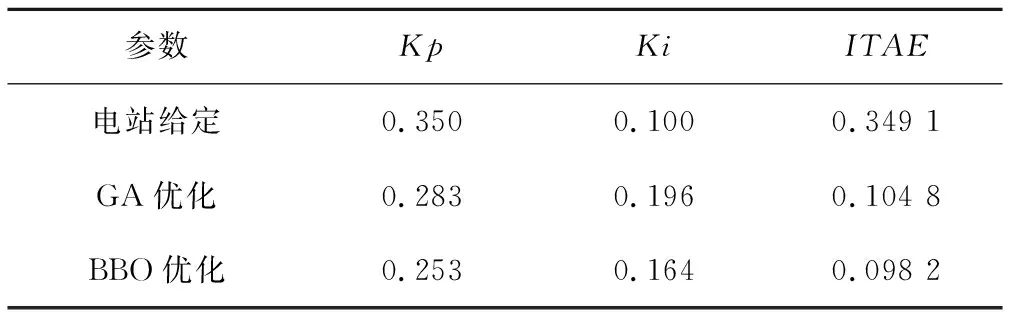
表3 优化的参数及指标Tab.3 Optimal parameters and corresponding indicators

(3)种群数量为80，迭代次数为100。从表4和图8可以看出，当种群数量为80 ，最大迭代次数为100次时，GA和BBO的ITAE指标进一步减小，分别为0.099 1和0.090 5，BBO的ITAE值最小。BBO对应优化参数的响应曲线上升时间短，超调量小，稳定最快，比电站预设和GA寻得的参数性能更优。

表4 优化的参数及指标Tab.4 Optimal parameters and corresponding indicators

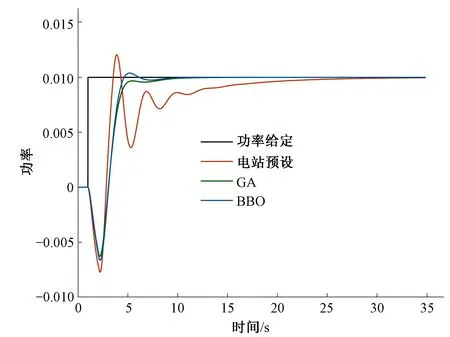
图8 1%功率扰动响应Fig.8 Time response of 1% power disturbance

总结上述对比结果，生物地理学算法在种群数量和最大迭代次数与遗传算法相同时，优化效果好于遗传算法，ITAE指标明显更小。

5 结 论

本文介绍了生物地理学优化算法原理及其数学模型，介绍了算法迁移和变异的流程，分析了生物迁移的模型。利用电站实际数据，结合实际控制参数和遗传算法，比较了生物地理学优化算法的寻优效果。对比试验的结果表明：①BBO算法的性能优于遗传算法，得到的PID控制参数控制效果比电站预设参数好；②随着种群规模和迭代次数的增加，由BBO算法得到的最优控制参数逐渐趋于稳定；③所选取的ITAE指标对超调量没有加以严格限制，在种群规模和迭代次数较少时，优化后的机组过渡过程仍会出现一定的超调。

□