基于遥感土壤湿度反演中尺度流域水储量季节性变化

2020-10-19谢冰绮吕海深朱永华

中国农村水利水电 2020年10期

谢冰绮，吕海深，朱永华

(1.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学水文水资源学院，南京 210098)

0 引言

陆地水储量(TWS)作为地表水和地下水综合测度，在地球气候系统和水资源管理中发挥着重要作用[1]。2002年3月，重力恢复和气候实验卫星GRACE的发射为TWS的计算带来新的途径，GRACE卫星能观测高精度地球重力场，在去除大气和海洋信号影响后，剩余信号与TWS高度相关[2]，可作为大型流域水量平衡计算中TWS变化验证数据集[3, 4]。GRACE数据原始空间分辨率较粗(3°×3°)，应用于小尺度区域会有较高的不确定性[5, 6]，因此推动了基于GRACE的水储量变化(dSg/dt)空间降尺度技术的发展，Schumacher等[7]基于陆面模型将GRACE产品降尺度到更高的分辨率， MIRO等[8]采用统计降尺度方法来获得空间分辨率更高的水储量变化。

土壤湿度与地表水和地下水的密切关系[9, 10]为直接估算TWS变化提供了新的思路，ABELEN等[11]研究发现，在潮湿和温带气候GRACE数据与的土壤湿度数据相关系数接近于1。基于此，Wade等[6]基于遥感土壤湿度水储量变化(dSm/dt)并证明其与dSg/dt在统计上具有显著相关性，能满足水量平衡方程，且在中尺度流域的应用情况良好。这说明遥感土壤湿度在研究水储量变化和流域水量平衡上具有一定的价值，特别是在空间尺度上比dSg/dt更具优越性。

淮河流域人口密集，土地肥沃，是我国重要的粮食生产基地，随着流域社会经济水平的提高，区域水资源的分配和利用面临极大压力，对流域内陆地水储量变化进行研究可为当地水资源规划、管理以及防洪减灾等提供一定的参考。本文首先基于水量平衡方程和GRACE数据在大尺度(吴家渡)流域(>15 000 km2)检验降水量、径流量及蒸散发数据集在本流域的适用性，在此基础上基于土壤湿度计算陆地水储量变化，讨论中尺度流域(2 000～15 000 km2)内季节性水储量变化dSm/dt在水量平衡分析中的效果，重点关注淮河流域吴家渡上游地区汛期(6-9月)或非汛期(10月-次年5月)前后水储量变化情况。

1 研究区概况

淮河流域位于中国南北气候过渡带，淮河以北属暖温带区，淮河以南属北亚热带区，淮河流域多年平均降水量约为920 mm，选择淮河流域吴家渡水文站以上集水区作为研究区，流域面积为12.133 万km2，具有分布合理的雨量站及具有高质量的遥感产品(图1)，在吴家渡流域内分别以班台、息县、蒋家集以及横排头为出水口，选择4个中尺度流域，四者沿西北到东南分布，年降水量依次增加(表1)。

图1 流域示意图Fig.1 Distribution of the basins

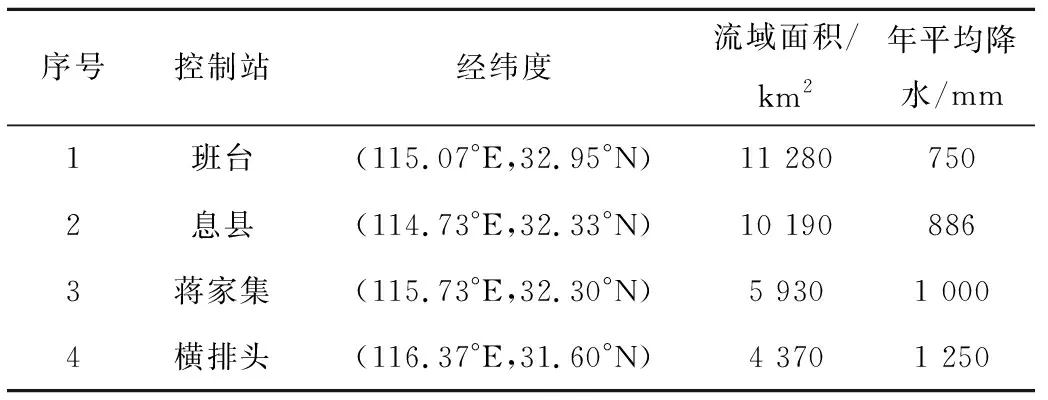
表1 中尺度流域属性表Tab.1 Attributes of medium-scale basins

2 材料与方法

2.1 数据及预处理

2.1.1 实测降水数据及径流数据

降水数据为中国气象数据集中82个地面气象观测站站点数据，使用泰森多边形法计算流域面雨量(P)。径流数据取吴家渡、班台、息县、蒋家集和横排头五个水文站的水文年鉴资料，并计算相应流域的径流深(Q)。

2.1.2 GLEAM蒸散发

本文所使用的蒸散发数据为全球陆地蒸散发阿姆斯特丹模型(GLEAM)计算得到的净蒸散发量。GLEAM模型基于具有物理机制的Priestley-Taylor公式，利用遥感获得的土壤湿度和植被密度等计算得到地表蒸散发数据[12]，在全球范围的月尺度上表现良好(相关系数达0.9)[13], 基于GLEAM 产品估算2001-2010年淮河流域降雨量的平均相对偏差在10%左右[14]，在水量平衡计算中具有优秀的性能。本文使用GLEAM v3.2 a版本，空间分辨率为0.25°，时间分辨率为1日，通过累加得到汛期与非汛期的总蒸发量，分别在各个流域计算格点均值得到流域蒸散发(ET)。

2.1.3 GRACE卫星数据

研究采用喷气推进实验室(JPL)发布的GRACE 卫星RL05M数据，该数据集滤除了来自2级处理的GRACE观测噪声及减少了海岸线上与陆地水文应用中的泄漏误差[15]。数据集的空间分辨率为0.5°，时间分辨率为1个月，数据集在2010-2015年共有59个月的数据，缺失的13个月数据通过线性内插获得，计算流域内格点均值得到流域水储量(Sg)。

2.1.4 遥感土壤湿度

本文使用欧洲太空局气候变化倡议(ESA-CCI)土壤湿度数据集v04.4融合产品，该产品以AMI-WS和ASCAT等散射计产品以及SMMR、AMSR-E、AMSR2和SMOS等辐射计产品为基础，利用合并算法[16]融合成长时间序列的土壤湿度数据集。数据的空间分辨率为0.25°，时间分辨率为1 d，计算流域范围内格点均值得到流域平均土壤湿度(θ)。

2.2 研究方法

2.2.1 水量平衡方程

研究中评估均基于闭合流域内的水量平衡方程：

P-Q-ET=dS/dt

(1)

式中：P、Q、ET分别为流域平均降水深、径流深和蒸散发量，mm，除了径流量外，忽略其他进出流域的侧向流量；dS/dt为流域水储量变化，mm、

水储量变化指汛期(Flood Season，FS)或非汛期(Non-flood Season，NFS)前后的蓄量变化，如2010年6月到2010年9月的水储量变化为2010年的汛期水储量变化。

2.2.2 数据集验证

由于降水、流量和蒸发数据集在一定程度上存在误差，需要先验证上述数据集在吴家渡流域的适用性。多项研究表明基于GRACE卫星反演获得大尺度流域水储量变化的精度较高，因此基于Sg在吴家渡流域进行水量平衡计算，验证数据集的适用性。其中，以汛期为例，基于GRACE的水储量变化dSg/dt计算如下：

dSg/dt=(Sg,Sept+Sg,Oct)/2-(Sg,May+Sg,Jun)/2

(2)

2.2.3 基于土壤湿度计算陆地水储量

SWENSON等[17]研究表明，陆地蓄水量对土壤湿度可能具有一定的延迟响应，本研究将(非)汛期最后一个月分为上中下旬，加权平均得到各个中尺度流域(非)汛期末的土壤湿度值。尽管GRACE数据代表的空间尺度较大，但仍可作为权重计算的参考，通过计算不同权重下的土壤湿度变化(dθ/dt)与dSg/dt的相关系数，获取合理的土壤湿度值：

θi=K1θ1,i+K2θ2,i+K3θ3,i

(3)

dθi/dt=θi-θi-1

(4)

式中：θi为第i个时期末各个中尺度流域的土壤湿度；θ1,i、θ2,i与θ3,i分别为i时期最后一个月的上中下旬土壤湿度值，m3/m3；K1、K2、K3为权重且K1+K2+K3=1；dθi/dt为第i时期的土壤湿度变化值。

得到土壤湿度变化量后需将土壤湿度变化转化为水储量变化dSm/dt，将单位由m3/m3转变为mm。这里引入转换系数Kpm缩放dθ/dt，与dSg/dt做标准差匹配：

dSm/dt=Kpmdθ/dt

(5)

Kpm=σ(dSg/dt)/σ(dθm/dt)

(6)

2.2.4 数据评估的统计学指标

为了定量评估基于土壤湿度计算得到水储量变化值的性能，本研究主要采用皮尔森相关系数(R)和均方根偏差(RMSD)作为评价指标，相关系数表示两个数据的线性相关度，R越接近1，相关程度越大；均方根偏差表示数据平均偏差程度，RMSD越小，表明两个数据越相近。

(7)

(8)

式中：dSi/dt表示第i时期的水储量变化，mm；(P-Q-ET)i表示第i时期计算的水通量变化，mm。

3 结果分析与讨论

3.1 数据集验证

选取吴家渡流域为验证区域，做水量平衡计算，图2为P-Q-ET和dSg/dt随时间变化图，2010到2015年间水储量的季节性变化范围在-200～150 mm之间，变化幅度较大，通常汛期表现为蓄水趋势，非汛期则相反。两者均在0附近波动且具有比较一致的变化，特别是在2011年汛期以前，水储量变化P-Q-ET与dSg/dt高度吻合。但部分季节存在表现不佳的情况，如2011年非汛期的P-Q-ET与dSg/dt数值差距较大、2012年非汛期的变化趋势相反等，这很大原因在于采用简单线性内插的方式来补充缺失的GRACE数据，造成了较大误差。P-Q-ET与dSg/dt的线性相关性为0.870(α=0.01)[图2(b)]，RMSD为47.3 mm，两者高度相关。以上分析可看出P-Q-ET和dSg/dt能使水量平衡方程成立，P、Q以及ET数据集具有一定精度，可用于后续中尺度流域水量平衡分析。

图2 吴家渡流域P-Q-ET和dSg/dt随时间变化图Fig.2 Seasonal time series of P-Q-ET and dSg/dt in Wujiadu basin

图3 P-Q-ET和dSg/dt相关关系图Fig.3 Relationship of P-Q-ET and dSg/dt

3.2 系数率定

通过计算所有可能的权重组合得，当K1=0.814、K2=0.185、K3=0.001时dθ/dt与dSg/dt相关系数最大，其值等于0.727。在不同权重组合下P-Q-ET与dθ/dt相关性均高于0.5，两者相关系数最大值分布有一定差异，但均与月初土壤湿度相关性较大。

(a)不同权重相下dSg/dt与dθ/dt相关关系图

(b)不同权重下P-Q-ET与dθ/dt相关关系图图4 不同权重相关关系图Fig.4 The impact of weighting factors on the correlation

通过标准差匹配法计算得Kpm=1 425 mm，为验证该方法的适用性，带入不同Kpm值计算4个中尺度流域dSm/dt与P-Q-ET的均方根偏差(RMSD)(图5)，当Kpm=1 517 mm时RMSD达最小值，与标准差匹配法结果相近，可直接使用该方法计算Kpm。

图5 不同Kpm对dSm/dt与P-Q-ET之间RMSD的影响Fig.5 The impact of different Kpm on RMSD between dSm/dt and P-Q-ET

3.3 中尺度流域内水量平衡分析

利用4.2.1的方法获取权重W与转换系数Kpm，计算班台、息县、蒋家集以及横排头4个中尺度流域的dSm/dt值。

图6 dSm/dt与P-Q-ET相关关系图Fig.6 Relationship between dSm/dt and P-Q-ET

dSm/dt与P-Q-ET相关性为0.645，RMSD为71.5 mm，呈显著相关。计算时将流域水通量P-Q-ET进行闭合计算，即认为各个流域水通量在六年内为0，将P-Q-ET数值减去六年均值，若不进行闭合计算其相关性会降低至0.443，但其相关性仍具有统计意义(α=0.01)。

图7 中尺度流域水储量变化时间序列图Fig.7 Time series of P-Q-ET, P-Q-ET(closed) and dSm/dt in medium-scale basins

班台流域位于流域北部，气候相较其他3个流域更加干旱，流域水储量P-Q-ET变化明显，与dSm/dt变化一致。2010年到2011年的汛期4个流域的dSm/dt变化明显，这与2010年底到2011年2月的旱情有关，旱情的影响令偏湿润的息县、蒋家集和横排头流域水储量明显降低。在没有极端天气的影响下，偏湿润地区的土壤湿度保持稳定，变化较小，2012年后，蒋家集、横排头dSm/dt变化不明显。从未进行闭合计算的P-Q-ET看，蒋家集流域有持续储水趋势，横排头流域蓄水量则有持续降低趋势，可能与流域内水库调节有关，也可能存在跨流域的地下水通量。在部分时期dSm/dt与P-Q-ET的变化趋势出现明显的不一致，如班台地区2014年的非汛期，P-Q-ET变化呈增加趋势，而dSm/dt呈下降趋势，除了土壤湿度数据本身具有的不确定性外，不排除季节变化对土壤湿度的影响使得反演的班台流域水储量呈一定规律变化。但根据另外3个流域的时间序列图看，在P-Q-ET大的时期，相应dSm/dt也较大，这体现出土壤湿度具有捕捉中尺度流域水储量变化的能力。

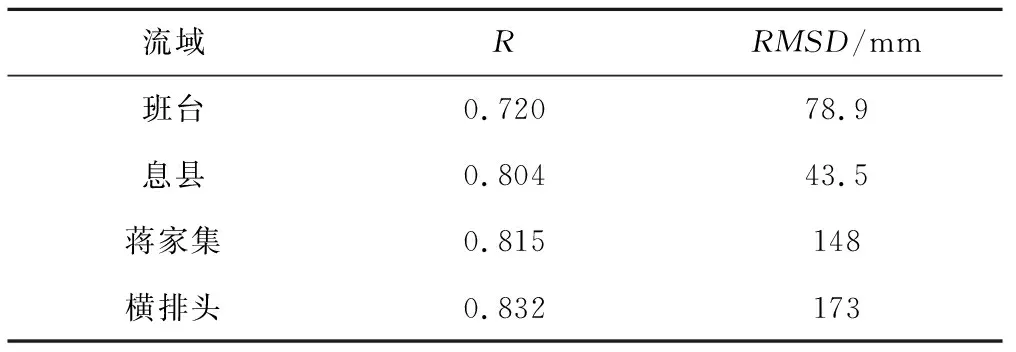
表2 统计指标Tab.2 Statistical indicators

从统计指标(表2)上看，各个中尺度流域上dSm/dt与P-Q-ET的相关系数均大于0.7，说明土壤湿度能捕捉流域水储量的变化。相关系数从北到南增大，RMSD在南部区域偏大，该方法虽然在湿润区捕捉变化的能力更强，但对量级的把握能力较弱，在北部偏干区域则表现呈相反趋势。

微波遥感获得的土壤湿度反映的只是表层土壤几厘米范围内的水储量变化，不能直接监测深层地下水或地表径流的动态水量变化，但作为陆气水分交换及地表地下水分交换的中间媒介，土壤湿度与两者关系密切[18, 19]，基于此建立的简单反演模型能初步利用土壤湿度反演水储量变化。ESA-CCI土壤湿度融合产品相较于其他遥感产品来说具有更长的时间序列，但其精度仍较差，遥感土壤湿度的精度问题也是目前水文过程研究中的一个重难点。此外，该方法也会受其他因素的影响，如抽水灌溉会影响表层土壤湿度的观测，调水工程的增加使侧向水通量的交换更加明显，土壤湿度与地下水之间的关系会随季节变化而变化[20]，这要求对反演方法和参数方案做进一步的研究。