基于断面比能和大数据的明渠量水方法及其应用研究

2020-10-19谢晓彤

中国农村水利水电 2020年10期

孔强，谢晓彤

(石家庄市冶河灌区服务中心，石家庄 050000)

0 引言

目前对明渠量水已有很多研究，主要集中在以堰流、孔流、明渠均匀流为理论基础的各种量水堰(槽)、渠系建筑物和标准断面等量水方法[1-3]。实际工程中，不同方法都有其特定条件[4]：如特设量水堰(槽)需要一定的水头；渠系建筑物量水对淹没度、收缩系数要求较高；设置超声波流速仪等直接测流时，仪表安装位置有诸多条件；标准断面要求有稳定的上下游水位等，当明渠水流无法满足条件时，可导致测流结果出现较大偏差，严重的还会产生水位壅高、泥沙淤积、过水能力降低等不利影响。

本文旨在研究一种新型双水位量水方法，用于具有较小流速、较缓纵坡的明渠量水。这种方法基于断面比能和大数据理论，结合明渠均匀流谢才公式，采取迭代法计算流量，既有较高测流精度，又有广泛适用性，具有以下特点：①以水力坡度代替渠道纵坡，更符合明渠实际流态；②以可变糙率取值代替固定糙率取值，有效降低渠道糙率系数受季节和水深等因素变化对量水精度的影响；③利用现有明渠标准断面，不改变明渠现状、不壅水、不淤积，投资较小，适宜性强④采用大数据迭代算法，量水精度高。经冶河灌区实际验证，与流速仪测流结果对比，测流误差在3%～5%左右。

1 研究方法

1.1 有关概念及定义

1.1.1 明渠恒定渐变流

明渠恒定渐变流是指在一定时段内水深、流速等要素只沿流程发生变化的明渠流态。实际中灌溉渠道水流总会受到边界条件影响，绝大多数都属此流态。目前对于明渠恒定渐变流尚无计算公式，但对于有足够长度的顺直棱柱体渠道，当流量沿程不变时，仍近似于明渠均匀流，可用谢才公式计算：

(1)

式中：Q为断面流量，m3/s；i为底坡；A为过水断面面积，m2；R为水力半径,m；C为谢才系数。

谢才系数C常用计算公式有曼宁公式：

(2)

巴浦洛夫公式：

(3)

1.1.2 断面比能

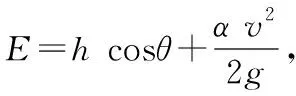
图1 断面比能示意图Fig.1 Sectional specific energy diagram

对于底坡|θ|<60的小底坡明渠[5]，cosθ≈1.0，渠道长度l≈水平距离l′,且i≈tanθ,h≈铅垂方向的深度h′=h/cosθ，断面比能公式简化后有：

(4)

式中：E为断面比能,m；h为水深,m；v为平均流速，m/s；g为重力加速度,m/s2。

1.1.3 水力坡度

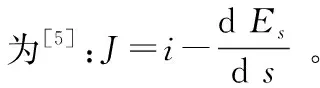
J=i+(Es-Ex)/L

(5)

式中：Es为上游断面比能，m；Ex为下游断面比能,m；L为上下游断面之间的长度,m。

1.1.4 大数据应用

大数据并非一个确切的概念，一种方式认为：大数据是人们在大规模数据的基础上可以做到的事情，而这些事情在小规模数据的基础上是无法完成的。从本质上，大数据中的“大”也不是绝对意义上的大，而是指不用随机(样本)分析法，而采用所有(整体)数据的方法，以认识事物的全貌[6]。在信息技术广泛应用的今天，大数据日益成为获得新认知、创造新方法的源泉。

大数据应用的重要环节是建立相关关系，利用服务器强大计算能力对全部测量数据进行数理计算，更快、更准的得出结果。基于此，在明渠上、下游水位与流量关联性基础上，以断面比能和明渠恒定渐变流理论公式，量化上、下游水位与流量之间的数理关系，对所有测量的上、下游水位数据进行大数据计算，进而得出符合精度要求的明渠流量。

1.2 流量求解

假定明渠量水段内水流流态符合条件：①水流流态为明渠恒定渐变流，且佛汝德数Fr<1；②上下游观测断面比能变化能准确反映水力坡度。

1.2.1 水力要素计算

首先计算明渠量水段的过水断面面积A、水力半径R、谢才系数C，其中，计算水深取上、下游实测水深平均值，糙率可根据明渠防渗形式暂按经验取值[5]。谢才系数采用式(3)，当R≤3 m时(灌区明渠水力半径多在此范围)，与实测资料相比，巴浦洛夫公式被认为是更为合理的公式[7]。

1.2.2 水力坡度计算

不考虑渗漏损失，则Q沿程不变，先假设上游断面平均流速vs与下游断面平均流速vx近似相等，即vs≈vx，由式(4)、(5)计算水力坡度可得：

J′=i+(Hs-Hx)/L

(6)

式中：Hs为上游断面水深，m；Hx为下游断面水深,m。

1.2.3 流量计算

按式(1)计算流量Q′，以式(6)计算得出的水力坡度J′代替i可得：

(7)

由流量Q′，返算上、下游断面平均流速vs、vx。将返算得出的vs、vx代入式(4)、(5)，重新计算水力坡度J″(含上、下游流速水头的断面比能)：

J″=i+(Es-Ex)/L

(8)

1.2.4 迭代求解

将式(8)中计算得出的水力坡度J″代替i，再次按式(1)计算流量Q″：

(9)

两次计算流量差|Q″-Q″|小于设定值时为最终计算流量，否则按本文1.2.3～1.2.4步骤重新计算，直到满足要求为止。

1.2.5 糙率调整

以流速仪实测水深、流量数据为准，调整1.2.1中的经验糙率取值，使最终迭代计算流量值与实测流量值相吻合。

2 工程实例

选取石家庄市冶河灌区某浆砌石矩形断面渡槽，渡槽内壁整洁无杂草、淤积，全段无水量流入、流出，内壁为旧的较完好的水泥砂浆抹面，渡槽原作为明渠标准段测水，因水位流量关系不稳定，误差在10%～15%。渡槽设计水深2 m，设计流量10 m3/s，在距渡槽进口和出口各75 m的两个断面安装远程雷达水位计观测水深，详见表1。

雷达水位计每10 min采集传输一组水深数据，2018年10月至2019年11月共获取25920组有效数据，本文选取10组作为表2、表3算例。

表1 明渠基本参数Tab.1 Basic parameters of open channel

表2 一次流量Q′计算(n=0.025)Tab.2 One-step flow calculation Q′(n=0.025)

表3 二步流量值计算Q″(n=0.025)Tab.3 Calculation of two-step flow value Q″(n=0.025)

首先按步骤1.2.1计算水力要素：过水断面面积A、水力半径R，谢才系数C。谢才系数C按式(3)计算，糙率n值暂取0.025[5]，见表2。

2.1 一次流量计算

按式(6)计算水力坡度J′,将J′代入式(7)计算一次流量Q′，见表2。

2.2 二次流量计算

由一次流量Q′计算上、下游断面平均流速vs、vx，按式(8)、(9)计算二次水力坡度J″和二次流量Q″,动能修正系数取α=1.05[8]，重力加速度取g=9.806 65 m/s，详见表3。两次计算流量差|Q″-Q′ |小于设定值时为最终计算结果，否则重复上述步骤进行流量迭代计算。

2.3 糙率n值修正

以上计算过程中，糙率n值作为巴浦洛夫公式的参数，取0.025是经验值，尚不能反映渠道真实糙率，须经流速仪实测加以修正。现场采用重庆华正LS25-1型旋桨式流速仪实测上游断面流量(选取0.95 m至1.9 m 5组实测流量值作为算例，详见表4)。由实测流量值Q实测返算确定糙率n值，见表4。

表4 糙率系数修正Tab.4 Correction of roughness coefficient

将修正后的n值代替之前暂定值0.025，重新计算得出两次计算流量差|Q″-Q′|小于设定值时，即为精度满足精度要求的最终流量。

3 结果与分析

3.1 水深流量关系

通过水深和流量变化规律，可将实例中流量Q与上游水深Hs、上下游水深差ΔH计算数据绘制成图表，见表5、图2(横坐标为水深，纵坐标为流量，曲线从下到上依次为ΔH=2、6、10、14、18 cm对应流量)，方便日常查用。

3.2 糙率取值

糙率系数作为计算过程中的可变参数，其取值直接影响测流结果。对于明渠渐变流，因水深、流速、季节等要素变化，糙率n值不为常量，其取值较为复杂，不同明渠的糙率系数及其变化规律不尽相同，要建立稳定的糙率系数与水深的关系就有困难[9]。

本研究以计算数据与实测流量拟合度为判别条件，返算确定糙率值。根据冶河灌区灌溉制度和北方季节，将本实例糙率值按时段和水深划分为4个状态、3个水深区间，共12个分区，分别取n值编入软件程序计算，见表6。

表5 Q～Hs～ΔH计算结果Tab.5 The calculation results of Q～Hs～ΔH

图2 Q～Hs～ΔH关系曲线 Fig.2 Relation curve of Q～Hs～ΔH

表6 糙率分级取值Tab.6 Roughness grading values

此糙率取值方法充分体现大数据分析的优势，对每一组水深实测数据都按12个分区进行判断，分别取值，实践证明是准确可靠的。本实验过程中，迭代计算较大差值出现在12个分区之间的边界处，原因主要是：水深划分范围尚不内能完全代表整个断面边壁糙率变化；流速仪观测数据量偏小，不能覆盖所有水深，应用过程中，需要不断累积流速仪实测数据，不断优化时段和水深分区。

返算糙率系数表明：实际工程中的明渠糙率系数既随水深变化，又随时段变化。其中又以时段对糙率的影响更为显著和规律，如表6中，糙率系数均值随状态变化规律为4<3<2<1，表明秋冬渠道输水能力显著高于春夏。通过对冶河灌区实验渠道内壁观察：水深0～1.2 m为光滑区，由于长时间处于水面波动影响以下，渠壁较光滑，基本没有淤积和苔藓等水生植物；水深1.2～1.6 m为水位波动区，由于受上下游灌溉影响，水面长时间波动，渠壁易出现膜状苔藓等植物；水深1.6 m以上为短时过流区，此区流量、流速较大，过水时间较1.2～1.6 m区域短，渠壁较干燥，基本无苔藓等水生植物，这也可以解释糙率系数随水深不规则变化的原因。

基于上述分析，相较于试验室内随水深、流速变化规律，实际工程中，时段和边壁条件对糙率系数的影响更为显著。糙率分区数量应根据渠道规模和输水周期具体分析确定，糙率分区越细化，糙率值精度相对俞高，实际工作中流速仪率定工作量也会俞大。

明渠量水实际中，对流速仪实测数据多少尚无明确要求，但流速仪观测数据在水深分布上应具有代表性，即流速仪观测数据尽可能覆盖明渠有效水深范围，在同一水深范围同一时段不需要太多实测值。另外，流速仪实测数据多少与渠道规模有关，小型渠道仅需要较少观测值即可，中大型明渠相对而言就需要对不同水深范围进行较多的流速仪实测。明渠历次流速仪实测值可累计使用，对于多年运行的渠道，其流速仪实测值数量足够满足本方法需要。

3.3 量水段条件

3.3.1 断面要求

断面为稳定、顺直、防渗较完好的棱柱形顺坡(i>0)渠道，渠内尽量没有淤积、杂草等。

3.3.2 水流流态

水流平缓，流速满足佛汝德数Fr<1。观测断面位置应避免建筑物或较大弯道影响，一般距离水流急变段不小于15～20倍最大水深为宜。若水面波动较大，宜设置观测井以获取平稳水深数据，使观测值准确反映明渠水深变化。

3.3.3 量水段长度

本方法中明渠量水段长度(观测断面之间距离)须满足理论计算中的两个假定条件：流态为明渠恒定渐变流；通过观测断面之间的比能变化能准确反映水力坡度。因此，要求量水段长度内的水头损失hw能产生足够壅水高度，同时渗漏损失较小：

(10)

式中：h设为满足最小壅水要求的水头损失；Q设为允许的最大渗漏流量。

(1)量水段长度估算。理论上水力坡度反映的是单位距离的水头损失，而与量水段长度L无关。但为了使观测断面水深读数能准确反映水深变化，必须有足够的壅水高度ΔH，如图3。

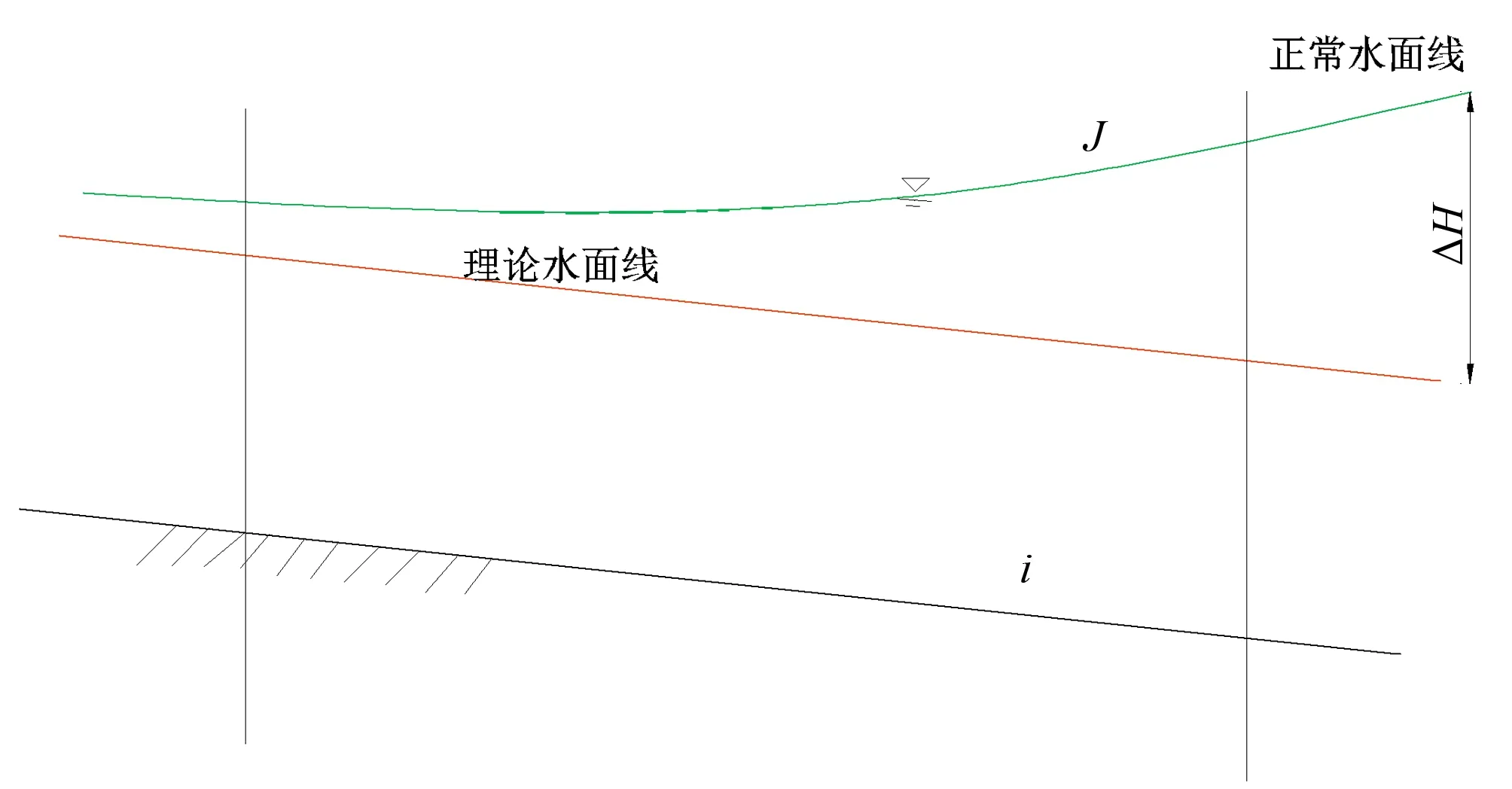
图3 明渠渐变流壅水曲线Fig.3 Backwater curve of gradual flow in open channel

将实际中的灌溉渠道水力坡度分为两种状态：①正常水力坡度状态：上下游既无流量流入，也无流量流出，此时水深沿流程增大，下游水深大于上游Hx>Hs，水力坡度小于纵坡Ji、J=i3种情况都可能出现。按状态②确定水力坡度较困难，按状态①来确定量水段长度更为可行，因此满足最小壅水要求ΔH的量水段长度L可表示为：

iL-JL>ΔH

(11)

由水力坡度定义：J=hw/L，则J=hf/L，计算中可略去局部水头损失只考虑沿程水头损失hf，代入上式化简可得：

(iL-ΔH)>hf

(12)

规范[4]中水深观测精度要求为±2 cm，可取Δh≥4 cm作为约束条件，Δαv2/2g应通过观测数据估算，流速较小时可忽略，据本研究数据，试算时ΔH可取5～7 cm。

沿程水头损失可用达西-魏斯巴哈公式与谢才公式相结合的经验公式计算：

(13)

通过实际观察，当L≥400 m时，明渠实验段出现较明显壅水。当L等于400 m时，误差小于4%；L大于600 m时，误差小于3%，表明本估算方法符合实际。量水段长度L=400 m时，L=200H(H为明渠最大水深)，远大于规范[4]要求的标准断面量水法最小长度。

量水段长度也可现场确定：测量正常状态上下游水深差值，壅水大于5～7 cm对应的渠段长度即可满足要求。

(2)渗漏损失估算。对于Q渗可用下式估算：

Q渗=qL

(14)

据冶河灌区渠道水利用系数资料测算，每公里渠道平均渗漏系数为0.004 4，折算 1 100 m长度渗漏系数为0.004 8，根据量水精度要求，量水段L内的渗漏系数应控制在小于1%之内为宜。

表7 量水段长度估算Tab.7 Trial calculation of water section length

综上，量水段的长度L应满足最小壅水高度的要求，同时不宜过长，否则渗漏损失、淤积、杂草、不均匀的纵坡等会对测流精度产生较大影响。

3.4 纵坡校核及流速仪率定

用于测流段的渠道纵坡，应以水准仪每隔20～50 m实测，绘制渠底纵断图，在实测纵断图上，取一条平均的纵坡线，作为计算纵坡，勘测时须向上下游适当延伸，以消除渠底不平整可能产生的纵坡误差，渠底较好的实测纵坡与设计纵坡基本一致。流速仪测流时，有条件的宜设置2～3台流速仪同时施测，取平均值。根据本实例，纵坡误差和流速仪实测误差是影响量水精度的主要因素。在日常量水中，应定期用流速仪观测，以校核糙率值。