大型雨水泵站进水流道水力特性研究

2020-10-19郁片红李君菡付小莉

中国农村水利水电 2020年10期

郁片红，李君菡，付小莉

(1.上海市城市建设设计研究总院(集团)有限公司，上海 200125；2.同济大学土木工程学院，上海 200092)

0 引言

泵站进水流道由前池和吸水室组成，前池是连接引水渠和吸水室的建筑物，其作用是让水流平稳且均匀地进入吸水室，为水泵提供良好的水流条件[1]。泵站进水流道设计不合理会造成不良流态，致使泵房效率低下，能耗变大，甚至产生涡流，直接影响泵房机组的正常运行[2-5]。因此，在泵站建设前分析其进水流道的流态是十分必要的。

随着数值模拟技术的快速发展，越来越多的学者将计算流体力学CFD和实际工程相联系，使其成为研究水体流动的重要手段之一[6-8]。本文以上海市宝山区张华浜雨水泵站作为研究对象，采用Fluent软件对泵站进水流道的流态进行数值模拟，分析前池水流流态，为优化泵站进水流道整流方案提供参考依据。

该雨水泵站分近远期实施，近期安装5台水泵，远期增加3台水泵。单泵设计流量为2.60 m3/s，水泵平均扬程为7.95 m。泵站前池长22.4 m，吸水室长5.5 m，喇叭口高度为0.68 m，前池扩散角为24°，池底坡度0.16，循环水泵喇叭口直径D为1.42 m。泵站结构图如图1所示，水泵编号顺水流方向从左至右为1～8号，并设立喇叭口中心线3.5D断面为分析断面。

图1 泵站结构图(单位：mm)Fig.1 Schematic structure of the pumping station

1 泵站水流特性研究

1.1 泵站流道模型建立

1.1.1 水流控制方程

泵站进水流道的流态属于充分发展的湍流流动，因此选用RNGk-ε紊流模型，其能较好地处理高应变率及流线弯曲程度较大的流动[6]。对于Re数较低的近壁区内的流动，则使用壁面函数法。

连续方程：

(1)

动量方程：

(2)

k-ε方程：

(3)

(4)

1.1.2 边界条件和网格划分

(1)边界条件。进口采用压力进口边界，出口边界取在水泵吸水管出口处，采用质量出口。自由表面则采用刚盖假定法简化处理，对于壁面区的流动采用壁面函数法处理。为提高流场计算的精度，对各工况分别建立模型，划分网格(见图2)，并通过了网格无关性检查。

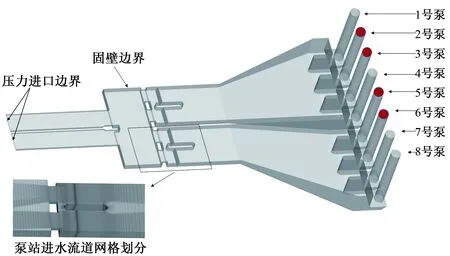
图2 泵站三维透视图及网格划分Fig.2 Grid of pumping station

(2)工况与初始条件。选择流速横向偏差较大的工况作为典型工况进行分析。开2、3、5、6号泵，总流量为10.40 m3/s，计算水深为3.3 m。模型进口处的湍动能k为0.006 5 m2/s2，湍动能耗散率ε为5.9×10-5m2/s3。

2.2 原设计方案数值计算成果分析

2.2.1 流道水力特性判别标准

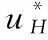
(5)

2.2.2 流态与流速分析

图3为设计方案下水深为3.3 m时不同切面的流线图，当水流从引水管道进入前池后，断面骤然扩大，致使流速减少，沿程压力增大。由于惯性力的作用，中间边壁附近的水流流速较大，主流未能扩散均匀，两侧形成偏流、回流及附壁涡。随着位置下移，吸水室前的漩涡数量增多，且深入到吸水室隔墩处。又由于吸水室内隔墩高度较矮，未超过设计水位，使得吸水喇叭口附近的水流出现大范围横流，易引发水泵振动、气蚀等现象，造成泵站效率降低、甚至不能正常工作的严重后果。

经过流速计算分析后发现流速分布的横向偏差几乎都大于30%，断面横向流速梯度也较大，流速稳定性较差，不利于水泵稳定运行。表1为水泵中心线上游3.5 D断面处吸水喇叭口悬空高度处的流速分布，断面最大流速为0.90 m/s，是最小流速的4.5倍；断面最大横向偏差出现在5号测点，其值甚至超过了125.7%，给水泵稳定运行带来不利影响。

图3 进水流道内不同切面流线图Fig.3 Streamlines of horizontal sections of inlet flow-passage

表1 吸水喇叭口悬空高度处的流速分布表Tab.1 Flow patterns on bell-mouth inlet

2 优化方案

通过上述分析可知，在原设计方案下，主流在前池内不能充分扩散，集中在中间隔墙附近。且各断面吸水喇叭口悬空高度处流速分布的横向偏差较大，对泵站稳定高效运行带来较大的隐患，需对进水流道进行结构优化。

2.1 整流方案制定

目前，关于泵站进水池的整流措施有很多，改变前池入流扩散角，在前池内设置底坎、衡梁和分流立柱，建设导流墩、导流墙等都是整流的有效措施[10]。其中导流墩控导干预均化水流的作用显著，且结构与形态易于控制，工程量较少，方便施工[10-12]，所以本文提出的整流措施以布置导流墩为主。

(1)优化方案1延长导流墩以改善泵站进水流道的流态，即两泵之间的导流墩增长至3.0 D断面处(距泵站后墙4.26 m)，并向下延伸至池低。

(2)优化方案2是在优化方案1的基础上，继续加长导流墩至3.5 D断面，同时将导流墩加高至设计高水位以上，使各吸水室前的水流完全分隔。

(3)优化方案3进一步改进，将进水口位置从整体正中进流改为单侧正中进流。

2.2 优化方案数值计算成果分析

2.2.1 流速流态分析

通过上文对原设计方案的分析，将优化方案的流线图与原设计方案的流线图(见图4)进行对比，3个优化方案的水流流态在吸水室处明显平顺，回流的范围显著减小。再分析比较3个优化方案的流线图[见图4(b-d)]：优化方案1中吸水室里大面积横流现象依旧存在。优化方案2中吸水室附近有大面积横流的问题明显改善。优化方案3中行进水流的主流充分扩散，不再集中于中间边壁，各吸水室内流速分布也较均匀，主流集中相对集中的问题得以解决。进一步分析流速等值线云图(见图5)后发现优化方案2与优化方案1相比，最大流速值并没有明显降低，流速分布的均匀度虽有提升，但并不显著。采用优化方案3后，主流充分扩散，不再集中于中间边壁，吸水室的流速分布也较均匀。

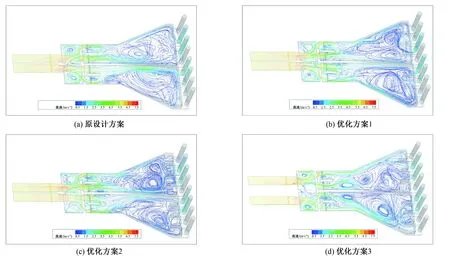
图4 整流前后进水流道流线图Fig.4 Streamlines of inlet flow-passage before and after rectification

图5 整流前后平面流速等值线云图Fig.5 Velocity contour of inlet flow-passage before and after rectification

表2为整流前后水泵中心线上游3.5D断面处吸水喇叭口悬空高度处的平均流速。分析可知：采用优化方案3改变进口流道位置后，吸水喇叭口悬空高度处的流速分布均匀度有明显提升，断面处最大流速是最小流速的1.68倍，比原设计方案减少了62.7%。表3为整流前后水泵中心线上游3.5D断面处吸水喇叭口悬空高度处的横向偏差值，原设计方案中断面最大横向偏差值为125.7%，优化方案1中断面最大横向偏差值出现在5号流道4号测点处，其值为104.1%，此位置处的横向偏

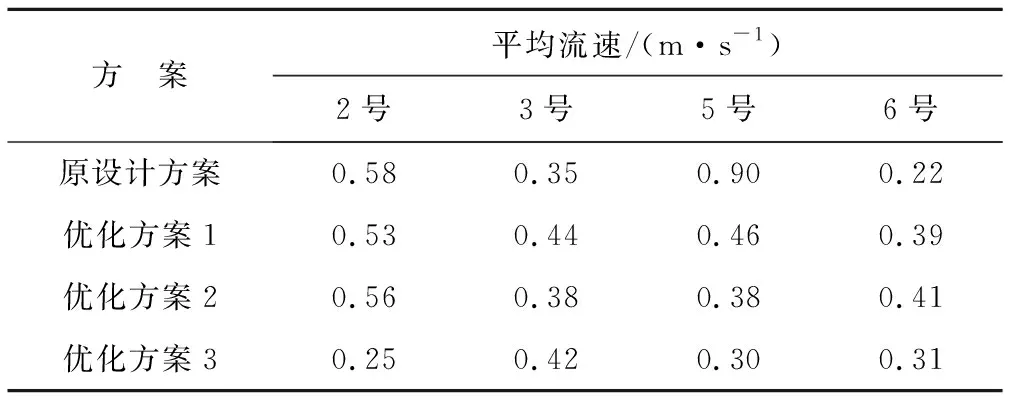
表2 整流前后的断面平均流速表Tab.2 Average flow velocity on bell-mouth inlet before and after rectification

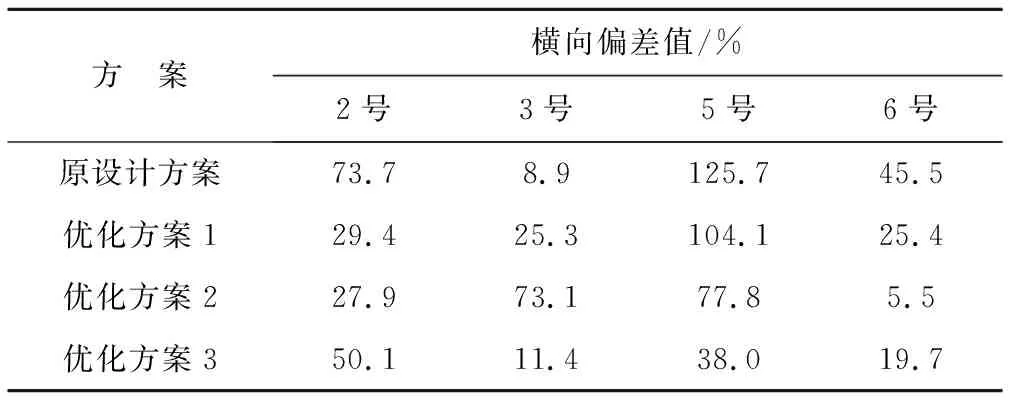
表3 整流前后断面横向偏差值Tab.3 Lateral velocity deviation on bell-mouth inlet before and after rectification

差值在优化方案2中降为77.8%。在优化方案3中，断面最大横向偏差值减少为50.1%，降低了76%。

2.2.2 湍动能及湍动能耗散率

湍动能大小表示水流脉动大小及混合程度的强弱，反映了流动的紊动强度，湍动能耗散率反映紊动所产生的能量耗散大小[13.14]。断面平均湍动能与耗散率沿程变化详见图6和图7。由图可见，水流在进入前池前的管道中，湍动能分布均匀且平均值较小；在流至前池入口前，湍动能和湍动能耗散率急剧变化，这是由于过水断面面积忽然变大，水流在此处发生剧烈碰撞，脉动及混合程度都急剧增大。当水流流进前池时，湍动能及耗散率均出现最大值，这表明水头损失主要集中在此段。水流进入前池后，在前段部分依然存在较强脉动。当水流沿前池继续前进时，由于流体的耗散效应及断面面积逐渐增大，水流流速逐渐降低且缓慢恢复到均匀分散的状态，湍动能和湍动能耗散率也沿程降低。