汽液黏滞系数对空化泡溃灭过程影响的数值模拟

袁晓龙，何小泷,汪凯迪

(1.雅砻江流域水电开发有限公司，四川 成都 610051；2.交通运输部天津水运工程科学研究所工程泥沙交通运输行业重点实验室，天津 300456；3.中国三峡建设管理有限公司，四川 成都 610023)

空蚀空化广泛存在于水利、航海、液压系统、人类体液循环系统这一系列工业与自然现象中[1-3]。空化泡溃灭过程中，由于空化泡内部压力与周边液体压力之间的压差剧烈变化，泡内汽体与泡外液体之间迅速转化，因此，空化泡的溃灭过程是带有复杂传热传质相变过程的流体力学问题。前人研究表明空化泡溃灭过程中产生的高温、微射流和冲击波的共同作用是空蚀破坏的主要原因。

常用的空化泡溃灭的研究方法有理论分析、试验研究和数值模拟。理论分析通常需要对问题作出许多简化，如Plesset等[4]采用Raleigh方程模拟空化泡溃灭时作出了以下假设：忽略表面张力、液体可压缩性、液体黏滞性等，这样的假设导致理论分析并不能直接用于实际的空化泡溃灭的研究中。而试验受限于测量技术，难以获得空化泡周边的速度和压力变化过程。随着计算机技术的快速发展，计算流体力学因其结果可以有效展示流场的演化过程，逐渐成为研究流体运动的重要手段。与试验研究相比，数值模拟可以有效地展示出空化泡在溃灭过程中微射流的形成。传统的空化泡溃灭研究的数值模拟方法主要分为基于Navier-Stokes方程和非理想流体状态方程的可压缩空化模型、基于Navier-Stokes方程和传质方程的不可压空化模型及可以模拟多空泡群的离散汽泡法。格子玻尔兹曼方法(LBM)作为一种介观数值模拟方法，从玻尔兹曼粒子动理学出发，能够有效模拟结晶、沸腾等带有传质相变过程的多相流现象。相较于传统数值模拟方法，LBM优势在于仅需要求解一系列线性方程组而避免了对流相的求解，同时压力与状态方程相关而避免求解泊松方程，且对于复杂边界处理十分简单[5]。

经过近30年的发展，现有 LBM多相流模型可以归纳为伪势模型[6-7]、颜色模型[8]、自由能模型[9-10]和相场模型[11]。其中伪势模型由Shan等[6]提出，该模型利用粒子间的相互作用力自动形成交界面，简化了汽液交界面的处理。Sukop等[12]利用伪势模型对各相异性条件下空化泡的生成开展了研究。Chen等[13]结合伪势模型与精确差分法(exact difference method，EDM)外力格式，模拟了液相与汽相的密度之比为67.5条件下空化泡在剪切流中的生长过程，其所得结果与Rayleigh-Plesset方程理论解吻合。Yang等[14-16]利用Bhantagar-Gross-Krood(BGK)模型与EDM外力格式相结合，模拟了液相与汽相的密度之比为30～50时单个空化泡的溃灭过程，获得了溃灭过程中压力场和速度场的变化。Shan等[17-18]进一步采用多松弛时间(multi-relaxation-time， MRT)碰撞算子模拟了液相与汽相的密度之比为750时空化泡的溃灭过程，模拟结果与Lauterborn等[19]的理论分析结果吻合良好。以上研究均证明LBM可以有效模拟空化泡的生长和溃灭过程。

黏滞系数对空化泡溃灭过程中形成的微射流和冲击波具有较大的影响，但当前利用LBM对空化泡溃灭过程的研究中并未考虑黏滞系数对空化泡溃灭过程的影响，而是将汽液黏滞系数比通常设为1。本文采用LBM模拟近壁区空化泡溃灭过程，分析不同汽相黏滞系数和液相黏滞系数对空化泡溃灭过程的影响，以及溃灭过程中产生的最大微射流流速、最大压力、最大溃灭时间的变化规律，为深入揭示空化泡溃灭机理打下基础。

1 数值模拟方法

基于BGK碰撞算子[20]，LBM伪势模型中粒子分布函数可以表示为

fi(x+eiΔt,t+Δt)=fi(x,t)-

(1)

(2)

粒子平衡态分布函数可以表示为

(3)

式中：ρ为宏观密度；ueq为平衡态分布速度；ωi为i方向的粒子平衡态分布函数的权重系数，对于D2Q9模型，当i=0时ωi=4/9，当i=1～4时ωi=1/9，当i=5～8时ωi=1/36。流场实际速度可以通过下式求得：

(4)

式中：u为宏观实际速度；FA为作用在粒子上的合力，包含粒子间相互作用力F和重力、向心力等体积力，F可采用Shan等[7]提出的公式计算：

(5)

式中：G为粒子之间作用强度；ψ为粒子之间的伪势；wi为权重系数，对于D2Q9模型，当i=0时wi=0，当i=1～4时wi=1/3，当i=5～8时wi=1/12[21]。根据Yuan等[22]的研究，引入非理想气体状态方程后，粒子间的相互作用势可以表示为

(6)

式中：pEOS为压强，可通过流体状态方程求得，本文采用Carnahan-Starling(C-S)状态方程[23]求解pEOS：

(7)

为满足热力学一致性，本文中外力采用Li等[24]提出的伪势模型外力项，其表达式为

(8)

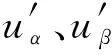
(9)

式中：ε为调节参数，用于满足模型的热力学一致性。密度场初始化如下：

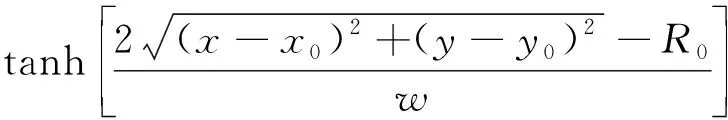
(10)

式中：ρl为初始液相密度；ρg为初始汽相密度；R0为初始半径；(x0,y0)为液滴中心；初始界面厚度w=5。

为研究流体黏滞系数对空化的影响，数值模拟中选取了不同松弛系数τ，如公式(11)所示[18]：

(11)

式中：τg为汽相松弛系数；τl为液相松弛系数；ρg、ρl分别为汽相密度和液相密度。

若无特别申明，文中所讨论质量单位为mu,长度单位为lu，时间单位为tu,速度单位为lu/tu，压力单位为mu·lu-1·tu-2。

2 模型验证

2.1 热力学一致性验证

为研究汽液黏滞系数比对模型的热力学一致性的影响，采用单松弛等温模型分别模拟了初始温度T0= 0.7Tc、0.8Tc、0.9Tc、0.95Tc条件下的汽液分离过程，计算结果如图1所示，图中νg为汽相黏滞系数，νl为液相黏滞系数。由图1可见，数值结果与理论解一致，在T≥0.7Tc条件下，改变汽液黏滞系数比不会影响数值模型热力学一致性。

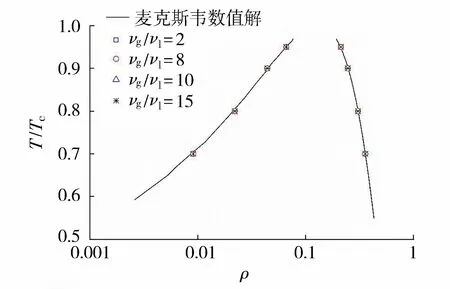
图1 汽液黏滞系数比对热力学一致性的影响

2.2 近壁区空化泡溃灭过程

为进一步验证模型的准确性，模拟了单个空化泡溃灭的演化过程，并与Philipp等[25]的试验现象进行对比。计算域为401 lu×401 lu正方形，空化泡初始半径R0=50 lu，计算域底部固壁采用标准反弹边界，左右均采用周期边界，顶部采用Zou-He压力边界[26]，计算区域如图2所示，图中P为液相压力，Pv为汽相压力。

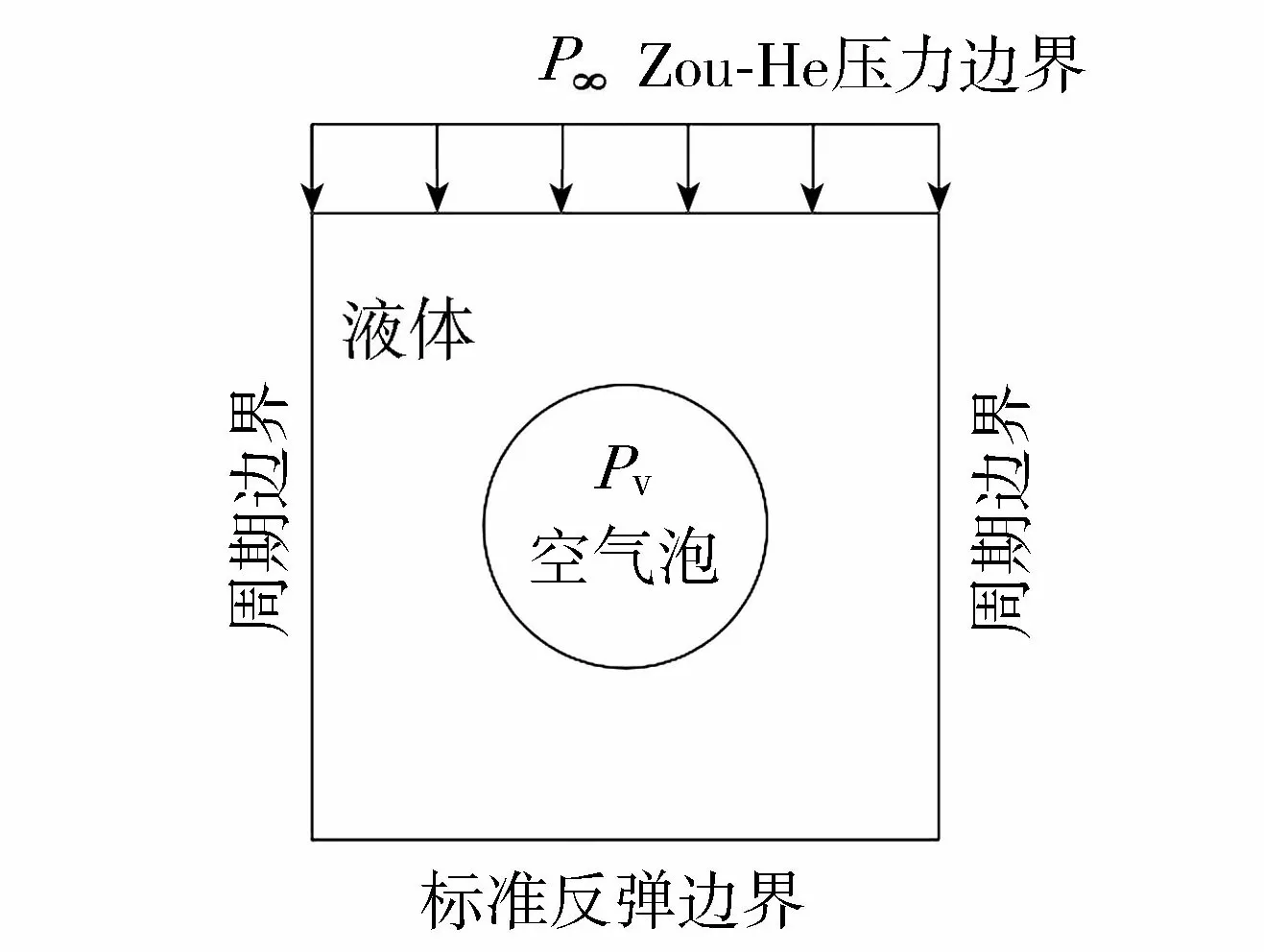
图2 计算域示意图

空化泡初始位置与试验相同，无量纲距离λ=d/R0，其中d为空化泡中心与壁面之间距离。汽相密度设置为0.009 mu·tu-3，液相密度设置为0.39 mu·tu-3，对应空化泡内外压差Δp=0.003 89 mu·lu-1·tu-2，初始温度T0=0.7Tc，同时假设初始空化泡位于静止水体中，因此计算域内初始流速均为0。

Philipp等[25]认为无量纲距离λ>2.2时，壁面对空化泡溃灭的影响可以忽略。本文选取两个无量纲距离λ=1.6和λ=2.5，与Philipp试验中使用的无量纲距离相对应。λ=1.6和λ=2.5时计算结果如图3和图4所示，两工况汽相松弛系数τg=1.062 5，液相松弛系数τl=0.187 5，对应的汽液黏滞系数比νg/νl=15。当λ=1.6时，受到壁面影响，近壁区在空化泡溃灭初始阶段，横向压缩速率远大于纵向压缩速率，在此阶段汽泡主要为椭圆形。随着空化泡溃灭的发展，空化泡顶部出现高压区，而空化泡与壁面之间压力较小，形成相对低压区。空化泡上下之间形成压力差，即Bjerknes力。在Bjerknes力的作用下，汽泡顶部出现凹陷，并伴随着微射流的形成，最终空化泡发生溃灭。而当λ=2.5时，空化泡处于壁面影响区外，由于空化泡与壁面之间距离过大，空化泡与壁面之间并不会出现相对低压区，空化泡上下形成的压差不足以使空化泡顶部出现凹陷。不同无量纲距离条件下，LBM数值模拟结果与Philipp等[25]的试验结果基本一致，验证了LBM模型的有效性。

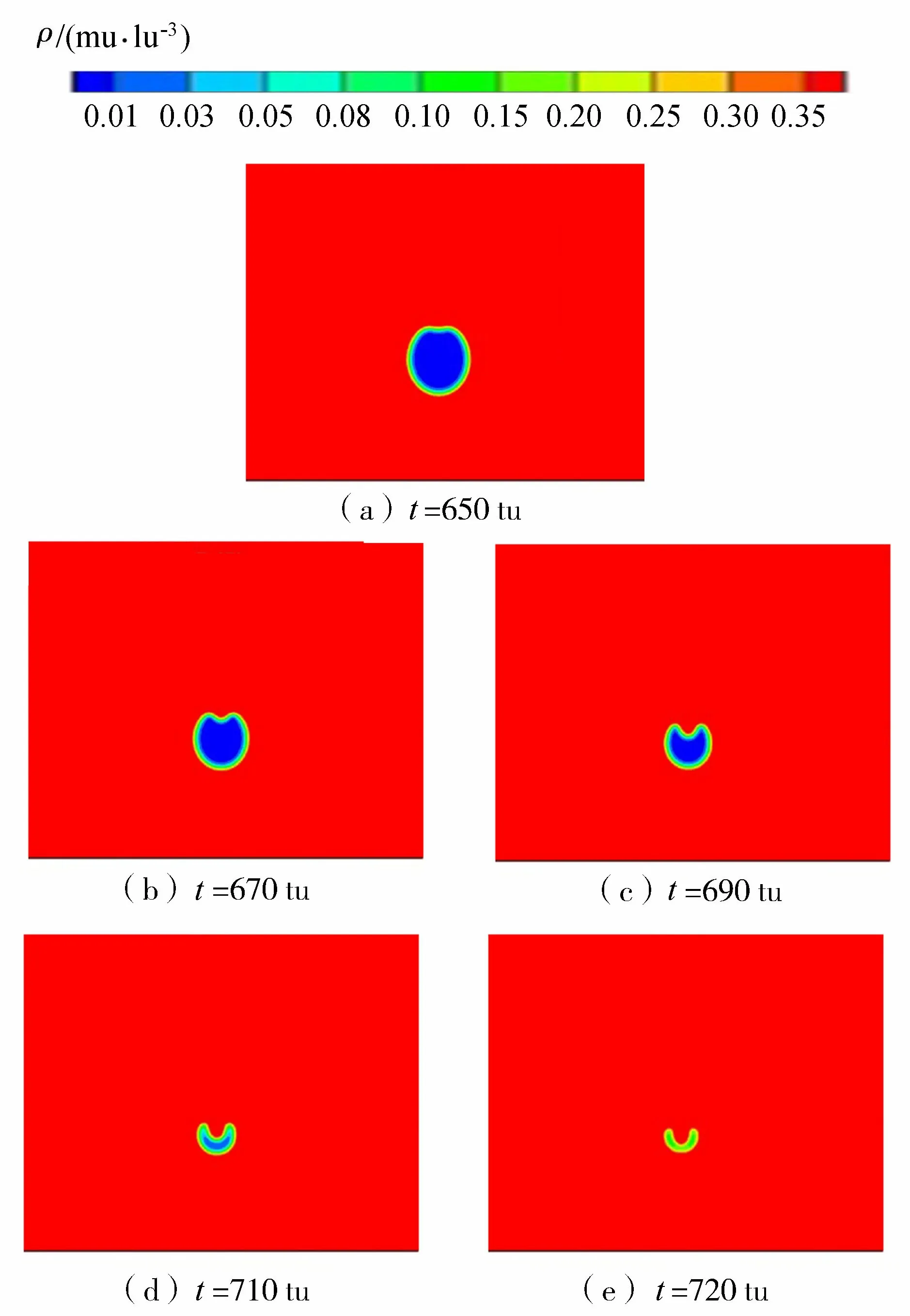
图3 λ=1.6时LBM模拟的空化泡形态演化过程

图4 λ=2.5时LBM模拟的空化泡形态演化过程

3 汽相和液相黏滞系数变化的影响

不同汽相和液相黏滞系数可以通过调节松弛系数τ获得。为研究汽相黏滞系数νg变化对空化泡溃灭过程中最大微射流流速umax、最大压强pmax、最大溃灭时间tmax的影响，选取不同汽相松弛系数τg和相同的液相黏滞系数νl如表1所示。不同汽相黏滞系数对最大微射流流速、最大溃灭压强及最大溃灭时间的影响如表1所示，可以看到改变汽相黏滞系数对空化泡溃灭时产生的最大微射流流速、最大压强、最大溃灭时间毫无影响，这是由于汽体质量较小，具有较小的惯性力。不同汽相黏滞系数条件下，空化泡溃灭时最大微射流流速为0.255 lu·tu-1，最大溃灭压强为0.007 18 mu·lu-1·tu-2，最大溃灭时间为721 tu。

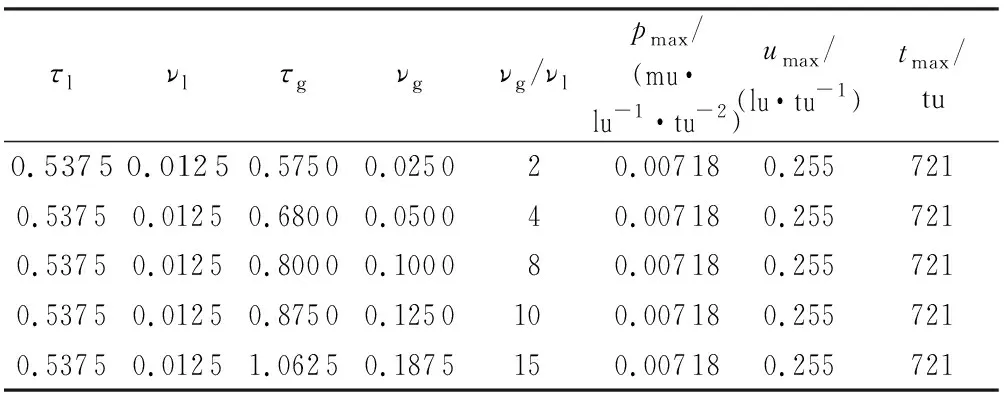
表1 汽相黏滞系数对空化泡溃灭的影响

为研究液相黏滞系数变化对空化泡溃灭过程中最大微射流流速、最大压强、最大溃灭时间的影响，选取液相松弛系数和对应的液相黏滞系数如表2所示。图5展示了液相黏滞系数对空化泡溃灭过程中最大微射流流速、最大溃灭压力和最大溃灭时间的影响，可以看出空化泡最大溃灭时间随着液相黏滞系数的减小而减小，而空化泡溃灭最大微射流流速和最大溃灭压强均随着液相黏滞系数的减小而增大，当液相黏滞系数由0.075减小到0.012 5时，空化泡最大压强由0.007 18 mu·lu-1·tu-2增加到0.010 03 mu·lu-1·tu-2，增加了39%，最大微射流流速由0.255 4 lu·tu-1增加到0.319 9 lu·tu-1，增加了25%，而最大溃灭时间则由721 tu缩短到680 tu。LBM数值模拟结果表明降低液体黏滞系数会在空化时产生更大的微射流流速和溃灭压强，与Popinet等[27]的试验所得结论一致。

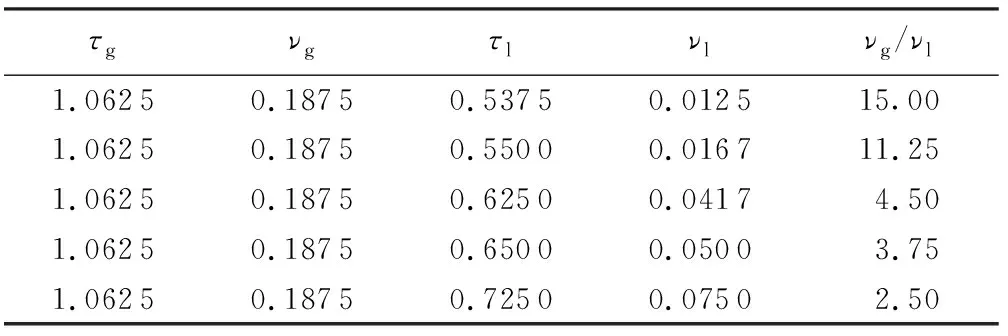
表2 液相黏滞系数对空化泡溃灭影响工况

图5 液相黏滞系数对空化泡溃灭的影响

4 结 论

a. LBM可以有效模拟近壁区空化过程，模拟结果可以有效观察到Bjerknes力的产生，并伴随着微射流的形成。

b. 由于汽相质量较小，具有较小的惯性力。相同液相黏滞系数条件下，改变汽相黏滞系数，空化泡溃灭时产生的最大微射流流速、最大溃灭压力和最大溃灭时间几乎不变。

c. 保持汽相黏滞系数不变，空化泡最大溃灭压强、最大微射流流速均随着液相黏滞系数的增大而减小，而最大溃灭时间随着液相黏滞系数的增大而增大。