一种新型异形椭圆无压隧洞断面的水力学分析
2020-10-18武周虎祝帅举
武周虎, 王 瑜, 祝帅举,2
(1.青岛理工大学环境与市政工程学院,山东 青岛 266033;2. 河南省城乡规划设计研究总院有限公司,河南 郑州 450044)
水工隧洞的断面形状是影响其水流条件、过流能力、围岩与支护结构强度及施工设计的重要因素。有压隧洞宜采用圆形断面,无压隧洞宜采用圆拱直墙式断面,若地质条件差,或洞轴线与岩层夹角偏小,宜选用圆形或马蹄形断面[1-2]。马蹄形包括标准马蹄形[3-4]、马蹄形(Ⅰ型,Ⅱ型,Ⅲ型,特型)[5-7]、平底马蹄形(Ⅰ型,Ⅱ型,特型)[7-9];还有蛋形包括半椭圆与半圆的上下组合型[10]、四圆弧蛋形[11]和六圆弧蛋形(Ⅰ型,Ⅱ型)[12-13]等形式;再有二圆弧仰拱曲墙式大断面水工隧洞[14]等形式。除圆形断面外,其他隧洞断面内轮廓线都是由圆弧、椭圆弧和直线等多段线采用相交或相切形式组合而成。
在隧洞断面设计中,围岩介质和初始地应力场等边界条件是客观存在不能改变,若水平地应力大于垂直地应力,宜采用高度小而宽度大的断面;若垂直地应力大于水平地应力,宜采用高度大而宽度小的断面,可以调整隧洞断面的几何形状、尺寸等参数,以改善围岩的应力分布及其稳定性状态[15-16]。虽然在这些隧洞断面内轮廓线的相交点处曲线连续,但一阶导数不连续;在相切点处曲线连续、可导,但一阶导数不光滑、二阶导数不连续。在相交和相切点处都将发生曲线的曲率突变,且在断面内轮廓线相交点处易产生应力集中现象,出现内力的极大值,受力条件变差[16]。这些隧洞断面形式的组合方式多样,内轮廓线形式复杂,水力设计的分区与计算公式烦琐,又各不相同,缺乏设计与建造的统一标准。因此,隧洞断面形状设计方案不是唯一的,而是有许多方案可供选择,由此就产生了优化问题[17]。
在无压隧洞断面设计中,当地质条件较好、山岩侧压力较小时,大多采用城门洞形;在其他情况下,采用什么样的断面形式常常存在多种选择。特别是马蹄形和蛋形断面多达10余种形式,具体选择由圆弧、椭圆弧和直线等几段线组成,圆心取在哪里、半径取多大、圆心角是多少、相交或相切点位置多高等,都要仔细分析、认真推算确定。无压隧洞的水力设计还需要根据断面曲线连接点位置,采用分区公式计算相应的水力要素。在优化调整无压隧洞的断面设计时,就需要重新进行断面形状与几何设计,还有水力设计、结构设计和衬砌施工设计等,其复杂性、烦琐性、工作量大等不言而喻。
本文基于宽阔河流中心稳定点源条件下保守物质等浓度线方程,以隧洞断面内轮廓线的最大高度和最大宽度为二参数,定义一种新型Wu’s曲线——异形椭圆,给出异形椭圆的标准方程以及形状分类,提出以异形椭圆作为无压隧洞断面内轮廓线的统一水力要素和均匀流计算方法,该方法的断面尺寸调整灵活,可为异形椭圆无压隧洞断面设计提供理论依据。
1 异形椭圆方程的由来及形状分类
1.1 由来
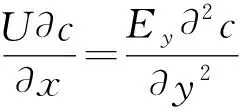
(1)
式中:x为自排放口沿河流流向的纵向坐标;y为垂直于x轴的横向坐标,坐标原点取在河流中心排放点;d为河流的平均水深;U为河流的平均流速;m为单位时间的保守物质排放质量;Ey为横向扩散系数。
武周虎等[20]在保守物质浓度c=ca=常数的条件下,通过对式(1)进行数学推演,给出了河流中心稳定点源条件下等浓度线所包围图形的最大长度Ls、最大半宽度bs和相应纵向坐标Lc分别为
(2)
在式(1)中取c(x,y)=ca,对根号下纵向坐标变量x除以Ls得到量纲一纵向坐标(x/Ls),同时乘以式(2)最大长度Ls右边的表达式;对横向坐标变量y除以bs得到量纲一横向坐标(y/bs),同时乘以式(2)最大半宽度bs右边的表达式,化简得到等浓度线方程(Wu’s曲线)为[21-22]
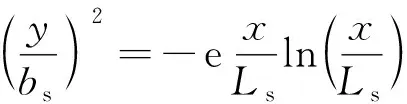
(3)
在研究中发现,式(3)所表示的等浓度线近似于椭圆形状,但只有单对称轴,笔者称其为“异形椭圆”。该曲线来源于保守物质平面二维简化对流扩散方程求解出来的浓度分布等值线,根据动量、热量和质量传递的相似性原理,可以推断应力与质量扩散之间也存在相似性关系,因此,该曲线极具学术研究价值。
1.2 标准方程与特征尺度定义
在式(3)中,将对称轴纵向坐标x改用对称轴垂向坐标z表示,定义异形椭圆对称轴垂向坐标z方向的最大高度为H=Ls,表示为隧洞断面高度;非对称轴横向坐标y方向的最大宽度为W=2bs,表示为隧洞断面宽度。则有异形椭圆标准方程为
(4)
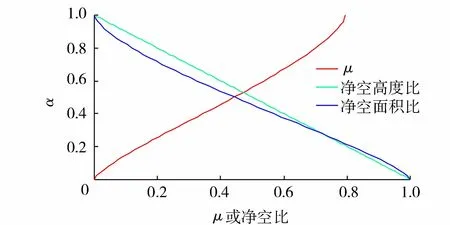
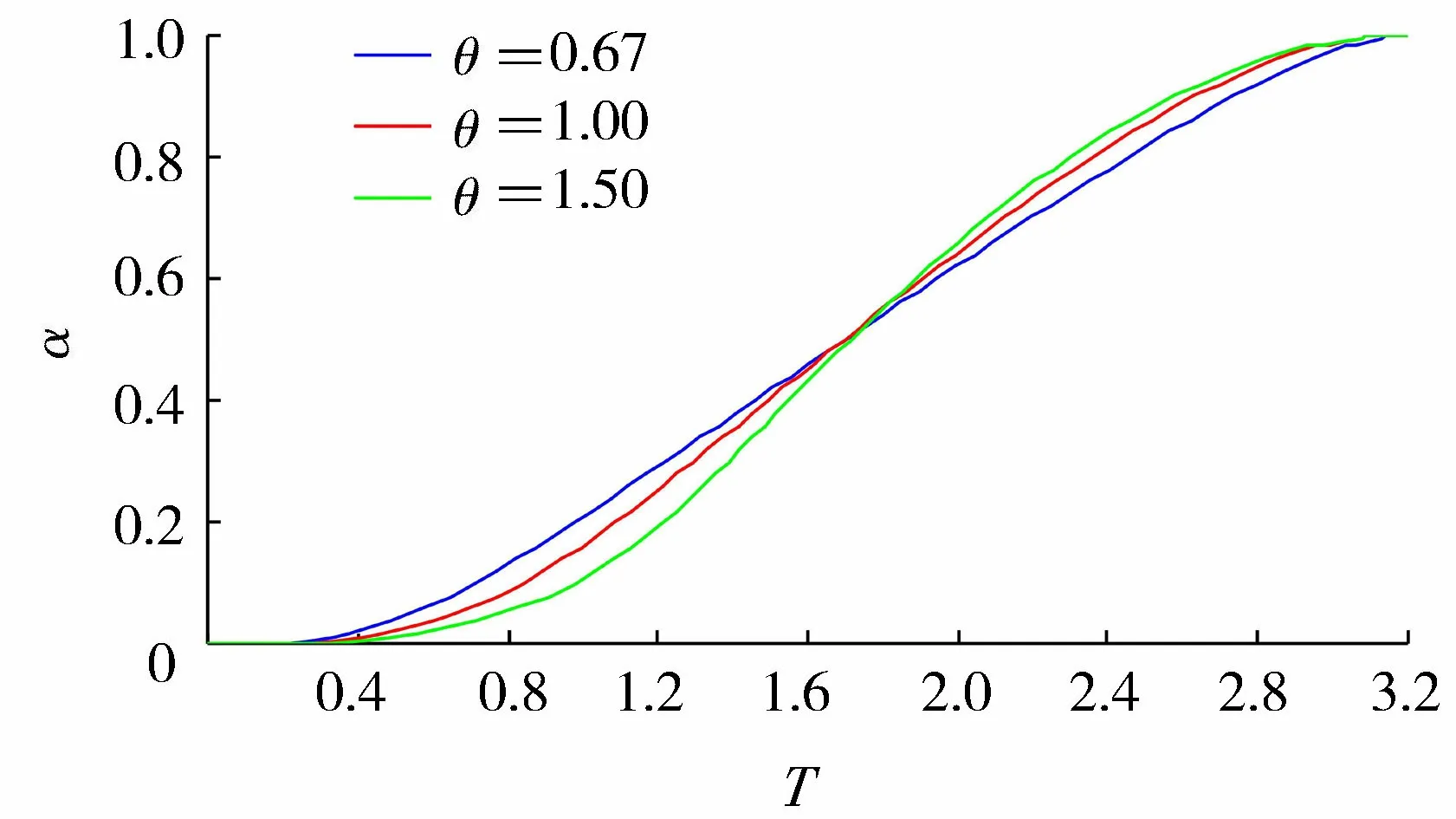
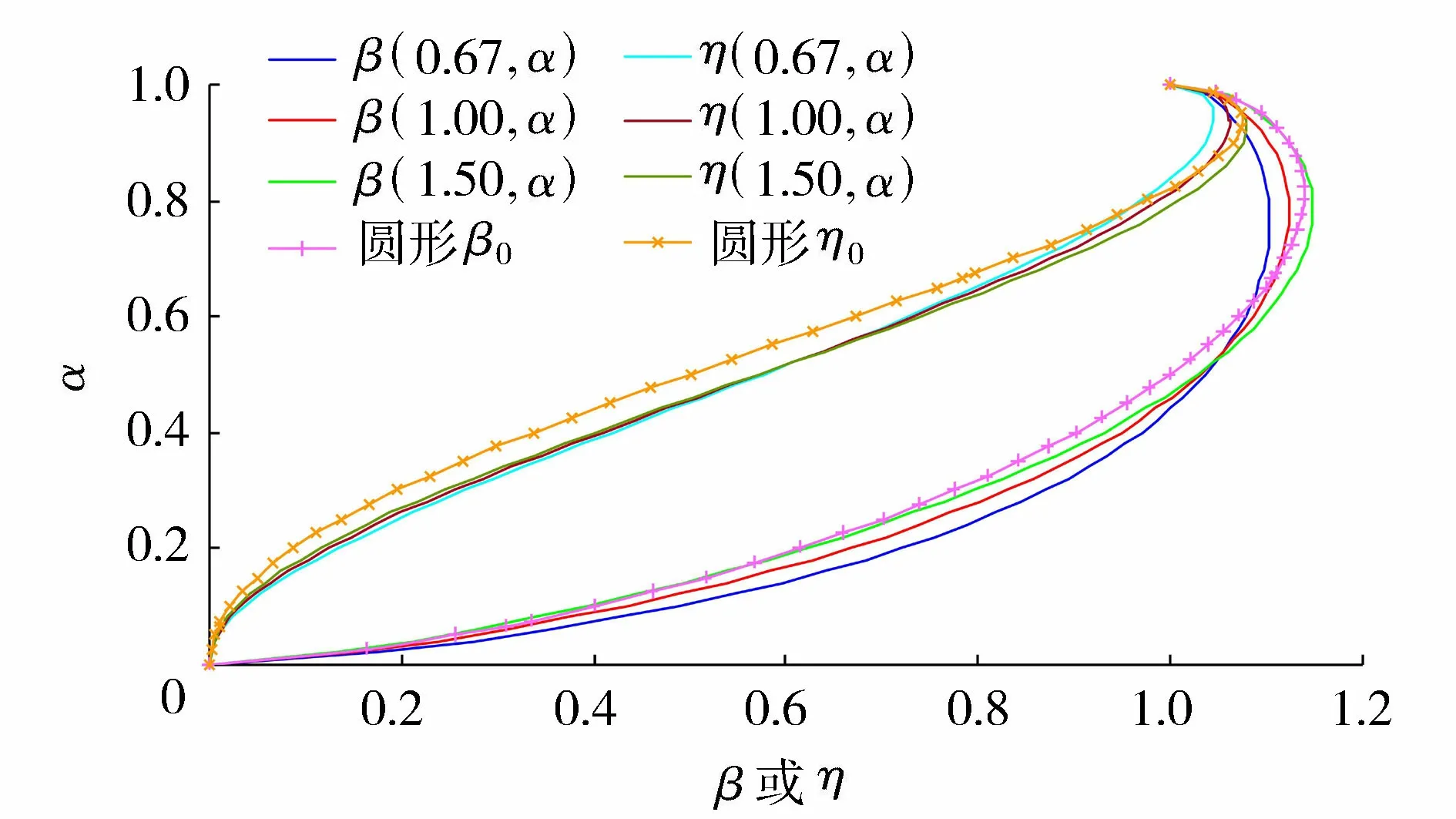
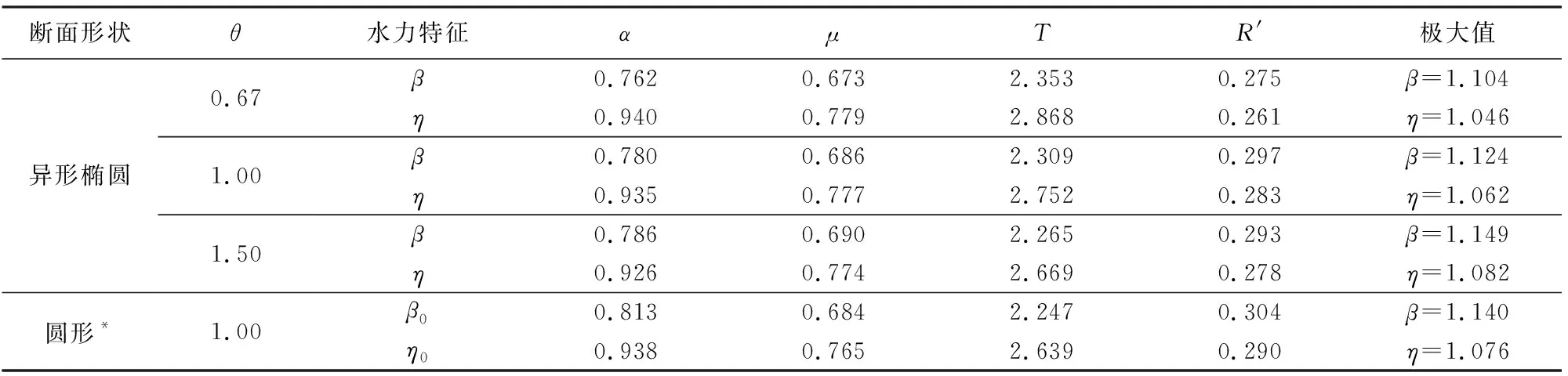
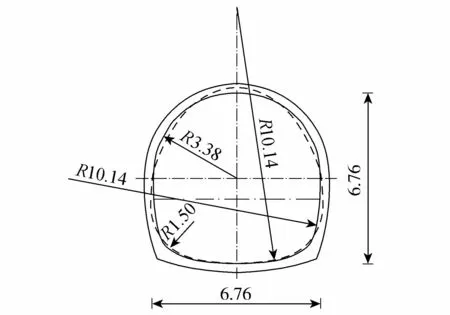
其定义域为:0 图1 异形椭圆断面及其特征尺度示意图 由图1可以看出,异形椭圆像一个变形椭圆,最大宽度线将整体分为上、下两部分,最大宽度线以上的高度占最大高度的0.632,接近黄金分割比例0.618,使图形产生美感。据此,提出异形椭圆(即WU型二参数曲线)水工隧洞断面的内轮廓线形状。 异形椭圆的压缩系数定义为非对称轴方向的宽度(或半宽度)与对称轴方向的高度(或半高度)之比,也就是异形椭圆的宽高比θ=W/H(θ>0)。图2为不同压缩系数时的异形椭圆形状示意图。 图2 不同压缩系数的异形椭圆形状示意图 由图2可以看出,异形椭圆的形状随压缩系数的增大是由高瘦逐渐变为宽胖,所以压缩系数可以反映异形椭圆的形状特征。据此,我们对异形椭圆的形状进行分类:当压缩系数θ=1时,异形椭圆的宽度等于高度,称为标准型;当0<θ<1时,异形椭圆的宽度小于高度,称为H型(高瘦型);当θ>1时,异形椭圆的宽度大于高度,称为W型(宽胖型)。 在隧洞内任一水深h时,则有充满度(即相对水深)α=h/H,由图1所示的异形椭圆断面的水力要素计算公式推导及有关特性曲线分析如下。 在式(4)中,令z=h,则有水面宽度B=2y,化简得到: (5) 由式(5)可以看出,异形椭圆断面的水面宽度与断面最大宽度成正比,其比例系数仅与充满度有关,该比例系数的变化规律类似于图1所示的断面形状。当α=1/e=0.368时,B/W的最大值为1.000;当α=0.500时,B/W=0.971;当α=0.750时,B/W=0.766。 将式(4)开平方,先导出y的显函数表达式,在z∈[0,h]区间上求定积分,再按对称图形面积乘以2,则得到异形椭圆过水断面面积A的积分表达式为 (6) 进行变量替换,令ζ=z/H,积分下限不变,积分上限变为α,则有: (7) (8) 式中:μ(α)为异形椭圆过水断面的面积系数。 对充满度α=1.0的满管流情况,令η=ζ1.5,积分上限为1,代入式(8)直接求定积分得到异形椭圆的满流过水断面面积系数(即隧洞断面面积系数)为 (9) (10) 该数值比椭圆的面积系数(π/4)大1.27%。 对充满度α<1.0的不满管流(无压隧洞)情况,异形椭圆的过水断面面积系数式(8)不存在直接积分值。可以借助于梯形法求定积分的公式计算过水断面面积系数: (11) 在式(11)中,将自变量ζ的积分区间[0,α]划分为n=1/Δζ等分,每一等分的长度Δζ取1.0×10-4,一般就可以实现数值积分值与理论值的误差绝对值小于1.0×10-5。若需进一步提高数值积分的精度,可以通过缩小等分长度或更换数值积分方法,如MATLAB求定积分的功能。在区间(0, 1)上给定一系列充满度α值,可以由式(11)计算出一系列相应的μ值,从而得到异形椭圆的过水断面面积系数μ与充满度α的变化曲线,见图3。异形椭圆断面无压隧洞的净空高度比(1-α)、净空面积比(1-μ/μ1)一并绘制于图3中。 图3 异形椭圆的过水断面面积系数和净空比变化曲线 由图3和计算数据可知,当α=0.5时,μ=0.442,则有异形椭圆的下半部分面积占隧洞断面面积的55.6%,上半部分面积占隧洞断面面积的44.4%;当α=0.273时,异形椭圆断面的净空高度比与净空面积比相等(0.727);当α>0.273时,在充满度相同条件下,异形椭圆断面的净空高度比大于净空面积比,有利于改善过流条件提高安全性。 按照水工隧洞设计规范[1-2]的规定,在低流速的无压隧洞中,若通气条件良好,在恒定流情况下,洞内水面线以上的空间不宜小于隧洞断面面积的15%。此时,异形椭圆断面净空面积比为0.15,相应的净空高度比为0.233,即对应异形椭圆断面无压隧洞的设计充满度不宜大于0.767。 对异形椭圆过水断面轮廓曲线进行积分,在隧洞内任一水深h时,则有异形椭圆的湿周χ为 (12) 式(4)两边对z求导,整理得到: (13) 将式(13)代入式(12),积分下限不变,积分上限变为h/H=α,并注意到W/H=θ,则有异形椭圆的湿周公式变为 (14) (15) 式中:T(θ,α)称为异形椭圆的湿周系数,它是异形椭圆压缩系数θ和过水断面充满度α的函数。类比数学上椭圆的周长定理,由式(14)定义异形椭圆的湿周定理:异形椭圆断面湿周等于异形椭圆断面湿周系数与异形椭圆半高度和半宽度之和的乘积。 下面分别针对标准型(θ=1.00)、H型(以θ=0.67为例)和W型(以θ=1.50为例)异形椭圆断面,在区间[0, 1]上给定一系列α值,采用数值积分方法,依次对异形椭圆断面湿周系数按照式(15)进行积分运算。据此,得到以θ为参变量的T随α的变化曲线如图4所示。 图4 异形椭圆断面湿周系数随充满度的变化曲线 由图4和计算结果可知,θ<1(H型)与θ=1(标准型)的T随α的变化曲线相比是先缓长后变为陡长,其交叉点以α=0.514为上界,随θ的减小而减小;θ>1(W型)与θ=1(标准型)的T随α的变化曲线相比是先陡长后变为缓长,其交叉点以α=0.514为下界,随θ的增大而增大。 对α=1.0的满管流情况,异形椭圆断面的湿周系数就是其周长系数(又可称为异形椭圆系数),由式(15)得到异形椭圆系数T1公式为 (16) 由式(16)可以看出,T1仅是θ的单变量函数。图5为θ=0.5~2.0时T1的变化曲线。 图5 异形椭圆系数随压缩系数的变化曲线 由图5和计算结果可知,一个有趣的现象是异形椭圆系数的最小值(T1=3.191)出现在θ=1.05处,而非出现在θ=1处。 当θ<1.05时,T1随θ单调下降;当θ>1.05时,T1随θ单调上升。当θ=0.5~2.0时,T1随θ变化关系的拟合曲线方程为 T1=0.088θ4-0.558θ3+1.350θ2-1.395θ+3.705 (17) 式(17)的相关系数为R2=0.999 6。 值得一提的是,当α=0.5时,不同压缩系数异形椭圆断面的湿周系数约占其异形椭圆系数的53.0%。 根据水力半径的定义:过水断面面积与湿周之比,由式(7)与式(14)相除,化简整理得到异形椭圆的水力半径R的计算公式为 (18) 其中相对水力半径R′为 根据异形椭圆断面面积系数μ(α)和湿周系数T(θ,α)的系列计算数据,由式(19)可得到以θ为参变量的异形椭圆断面相对水力半径随充满度的变化曲线,和以充满度为参变量的相对水力半径随压缩系数的变化曲线,见图6。 图6 异形椭圆断面相对水力半径变化关系 由图6可知,在θ不变的情况下,R′随α的变化曲线存在一个极大值点。 由图6(b)还可以看出,在α=0.75时的R′与其极大值随θ的变化曲线非常接近,最大相对差值仅为-0.2%。说明α=0.75(相应的净空面积比0.166>0.15,符合文献[1-2]的规定)时的R′近似为最大值,这是一种比较理想的水力工况。 0.553θ+0.048 (20) 式(20)的R2= 0.999 7,适用于θ=0.5~2.0范围。 根据水力学原理,均匀流的流速v与流量Q分别为 (21) (22) 式中:C为谢才系数;i为比降;n为糙率。 为便于分析异形椭圆断面均匀流的水力学特性,使其具有普遍意义,能适用于不同断面尺寸、不同糙率的情况,采用量纲一来表示。若不满管流的流速为v,满管流的流速为v1,则流速比β为 (23) 若不满管流的流量为Q,满管流的流量为Q1,则流量比η为 (24) 在式(23)和式(24)中,不满管流的面积系数由式(8)或式(11)确定;满管流的面积系数(μ1为常数)由式(10)确定;T(θ,α)由式(15)确定;T1由式(16)或式(17)确定。因此,流速比β和流量比η均为θ和α的函数。图7为异形椭圆和圆形断面均匀流流速比和流量比的特性曲线比较,表1为异形椭圆和圆形断面均匀流流速比和流量比极大值点对应的水力要素。 图7 均匀流流速比和流量比的特性曲线比较 由图7和表1可知,当α= 0.457和α= 0.812时,θ=1的标准型异形椭圆断面均匀流的流速比和流量比分别等于满管流的相应值。θ<1(H型)与当α<0.681时,θ=1的标准型异形椭圆断面均匀流的流速比大于圆形断面的相应值。当α>0.681时,标准型异形椭圆的流速比小于圆形断面的相应值;当α=0.780和α=0.813时,标准型异形椭圆和圆形断面分别达到最大流速比β=1.124和β0=1.140。当α<0.849时, 标准型异形椭圆的流量比大于圆形断面的相应值,当α>0.849时,标准型异形椭圆的流量比小于圆形断面的相应值;当α=0.935和α=0.938时,标准型异形椭圆和圆形断面分别达到最大流量比η=1.062和η0=1.076。 表1 均匀流流速比和流量比极大值点对应的水力要素 θ=1(标准型)的异形椭圆断面流速比和流量比随充满度的变化曲线相比,均是先陡长后变为缓长达到最大值再迅速减小到满管流的相应值;θ>1(W型)与θ=1(标准型)的异形椭圆断面流速比和流量比随充满度的变化曲线相比,均是先缓长后变为陡长达到最大值再迅速减小到满管流的相应值。 按照水工隧洞设计规范[1-2]无压隧洞断面净空面积不宜小于15%,其高度不应小于400 mm的规定,对应85%的过水断面面积,经计算异形椭圆和圆形断面相应的最大充满度分别为0.767和0.793,前者的相对净空高度较大,更容易满足。由上述分析可以看出,在充满度小于最大充满度的条件下,标准型异形椭圆比圆形断面具有更大的流速比和流量比,即在相同设计条件下标准型异形椭圆比圆形断面过流量大。由图7还可以看出,在相同设计条件下对压缩系数0.67≤θ<1的H型和1<θ≤1.50的W型异形椭圆断面同样具有比圆形断面过流量大的优点。 对于具有结构支撑的挖掘,压缩系数θ一般取原位应力比的平方根[24];压缩系数θ=1的标准型异形椭圆与圆形断面的独立变量个数相同。 在引汉济渭工程秦岭黄三段无压隧洞断面设计中,Q=70.0 m3/s、i=1/2 500、n=0.014。罗涛等[25]经对圆拱直墙形、圆形和标准马蹄形断面的综合比选分析,推荐采用马蹄形Ⅱ型(带倒角)断面:其顶拱内缘半径R1=3.38 m,圆心角180°;侧拱内缘半径R2=10.14 m,圆心角11.41°;底拱内缘半径R2=10.14 m,圆心角22.82°;侧拱拱脚处倒角半径R3=1.50 m,圆心角67.18°。据此可知,该无压隧洞内轮廓线的最大宽度与最大高度都为6.76 m,总面积A1=38.43 m2,其断面形状及尺寸见图8,相应的设计水力要素特征值见表2。 表2 等效异形椭圆与马蹄形Ⅱ型断面水力要素特征值比较 图8 等效异形椭圆与马蹄形Ⅱ型断面比较(单位:m) 根据罗涛等[25]在引汉济渭大型深埋无压隧洞断面优化设计中,给出的引汉济渭工程黄三段无压隧洞马蹄形Ⅱ型断面的设计资料,选用等面积标准型异形椭圆断面进行水力学分析,并与马蹄形Ⅱ型断面进行比较分析。 在引汉济渭工程黄三段无压隧洞设计流量、比降和糙率不变的条件下,选用与黄三段马蹄形Ⅱ型断面相应的等面积标准型异形椭圆断面(以下称为等效异形椭圆断面)进行对比分析。即等效异形椭圆断面与黄三段马蹄形Ⅱ型断面的总面积相等(A1=38.43 m2),且压缩系数θ=1。由异形椭圆的面积公式(7)和面积系数μ1反推计算得到等效异形椭圆断面的最大宽度与最大高度都为6.95 m,其断面形状见图8中虚线,zw=H/e=2.56 m处的点划横线表示最大宽度的位置高度。 下面要解决的问题是:已知Q、H、θ、n、i,求α。即求等效异形椭圆无压隧洞断面的水深h。首先,计算满管流的流量Q1,由式(22)得到: (25) 代入A1和R1的表达式化简得到: (26) 再代入相应的数值,得到θ=1时等效异形椭圆无压隧洞断面满管流的流量Q1S=79.16 m3/s。 其次,由式(24)得到相应的设计流量比ηS=0.884,再由图7查得相应的充满度αS=0.707,则有等效异形椭圆无压隧洞断面相应的水深为hS=4.91 m。 最后,依次计算等效异形椭圆无压隧洞断面的过水断面面积、湿周、水力半径、流速、净空面积比和净空高度,具体数值见表2。 由表2可以看出,等效异形椭圆无压隧洞断面的过流能力能够满足《水工隧洞设计规范》[1-2]的规定,等效异形椭圆与罗涛等[25]推荐采用的马蹄形Ⅱ型(带倒角)无压隧洞断面的水力要素特征值非常接近,前者的净空高度增加了8.5%,水力要素其他特征值的最大相对误差绝对值只有2.8%。 a. 基于河流中心稳定点源条件下保守物质等浓度线方程,定义了一种新型Wu’s二参数曲线——异形椭圆,以隧洞断面内轮廓线的最大高度H和最大宽度W为二参数,给出了异形椭圆的标准方程。据此,提出的异形椭圆隧洞断面是由一个独立二参数方程表征的完整连续与导数光滑曲线。 b. 以隧洞断面的宽高比(压缩系数θ=W/H=1)为判据,给出了H型、标准型和W型异形椭圆的形状分类;推导出了异形椭圆无压隧洞断面的水面宽度、过水断面面积、湿周、水力半径等水力要素的理论计算公式,其表达式均为统一连续函数,无须采用分区函数表述,断面尺寸调整灵活,在无压隧洞断面设计中更具优势。 c. 当无压隧洞断面净空面积比满足大于15%的规定时,标准型异形椭圆的流量比大于圆形断面的相应值。即在相同设计条件下标准型异形椭圆比圆形断面过流量大,前者的相对净空高度也较大,有利于改善过流条件提高安全性。 d. 给出的异形椭圆断面不满管流与满管流时流速比和流量比的理论计算公式及曲线图,适用于不同规格的断面尺寸、压缩系数、糙率和比降,计算简单快捷、方便实用,为该断面的水力设计提供了理论依据。 e. 实例分析表明,等效异形椭圆与马蹄形Ⅱ型(带倒角)无压隧洞断面的水力要素特征值非常接近,前者的净空高度增加了8.5%。因此,异形椭圆断面可作为一种新型的输水隧洞断面形式,极具学术研究和应用价值。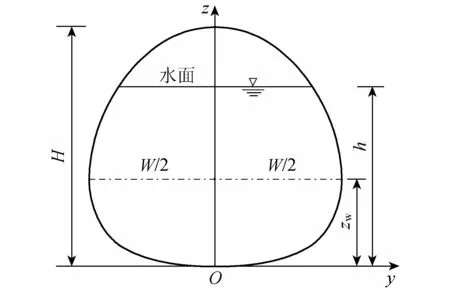
1.3 压缩系数与形状分类
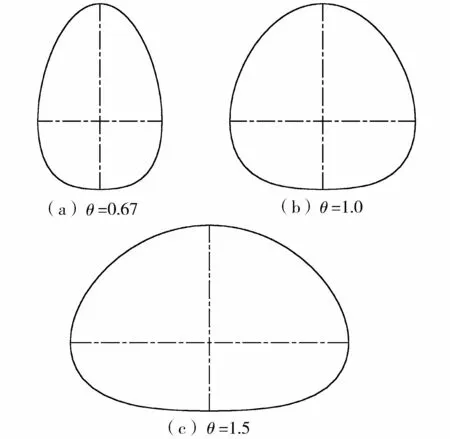
2 异形椭圆断面水力要素计算与特性分析
2.1 水面宽度
2.2 过水断面面积
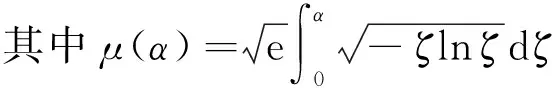
2.3 湿周
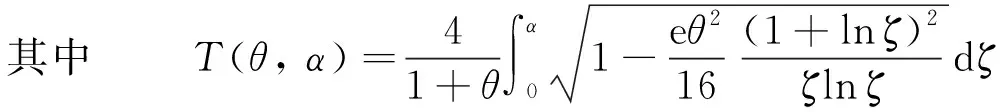
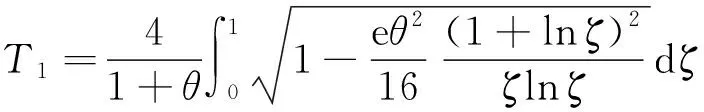
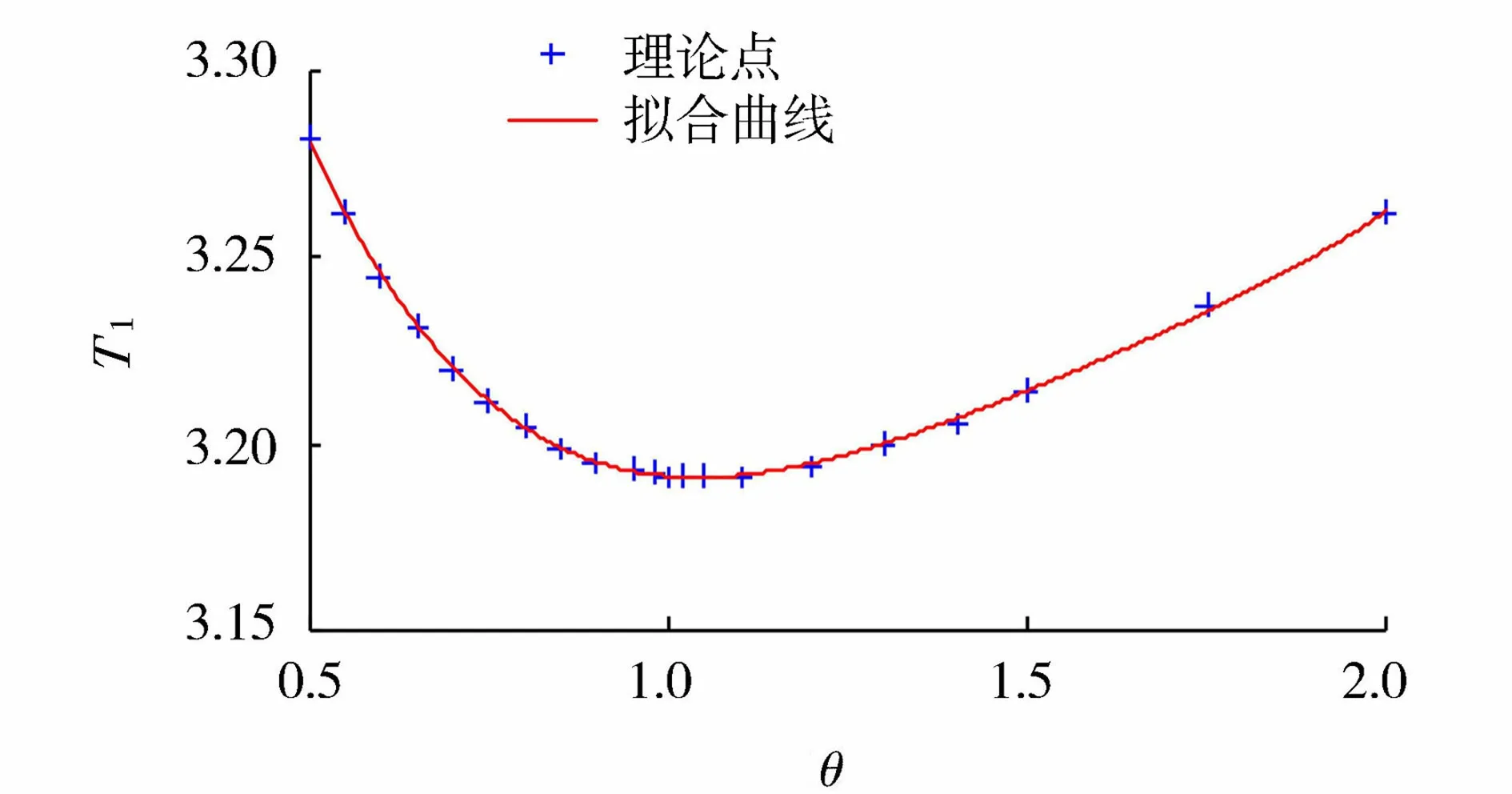
2.4 水力半径
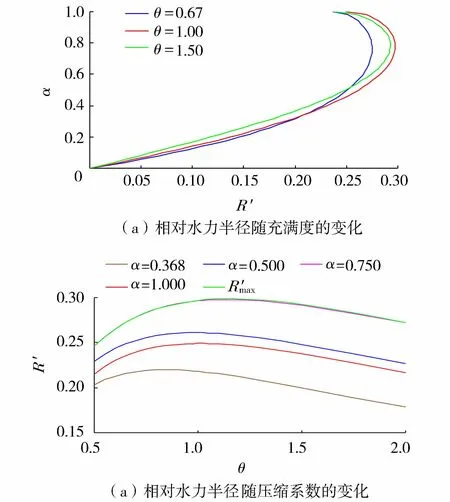
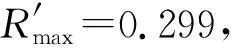
3 异形椭圆断面均匀流特性分析
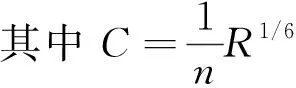
4 实例分析

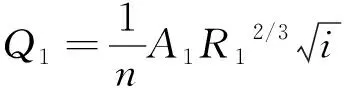
5 结 论
