烟叶松散回潮工艺参数和出料质量的贝叶斯网络模型构建与预测
2020-10-18文里梁何邦华林文强曾仲大
唐 军 唐 丽 文里梁 何邦华 林文强 曾仲大 马 宁 周 冰
(1. 云南中烟工业有限责任公司,云南 昆明 650231;2. 大连达硕信息技术有限公司,辽宁 大连 116023)
松散回潮是卷烟制丝工艺中的关键工序之一,其主要作用是增加烟片含水率和温度,提高烟片的耐加工性,松散烟片,并减轻杂气、刺激性,改善细腻程度[1]。松散回潮工序一般采用密闭滚筒式加工设备,主要涉及烟叶松散、喷嘴雾化加湿、蒸汽和循环热风增温等复杂过程,具有工艺参数多、影响因素复杂、规律摸索难等特点。陈杰等[2]研究了回风温度、工艺蒸汽系数等对烟叶物理质量舒展率的影响;邵惠芳等[3]研究了回风温度对烟叶化学成分与中性致香物质的影响;高翔等[4]研究了热风温度对烟叶内在质量的影响;唐军等[5]研究了回风温度对成品烟丝致香物质的影响;邓国栋等[6]研究了回风温度对烤烟烟叶感官特性的影响。李秀芳[7]开展了松散回潮关键工艺参数过程控制系统的优化设计,通过回风温度和含水率控制结构,优化其工艺参数,使松散回潮出口烟叶温度和含水率的波动减小,出口含水率平均标偏从0.43% 降至0.24%;范勇等[8]运用回归分析法对松散回潮出口烟叶含水率控制方法进行了优化研究,发现采用分类别差异性初始含水率控制模式能减少过程波动,进而提升出口烟叶含水率的稳定性;容秀英等[9]研究了烟叶松散回潮热风温度极值的控制方法,发现采用两极控制图(L-S控制图)法能有效提升热风温度的稳定性。目前,中国对烟叶松散回潮的研究主要集中于工艺参数回风温度和热风温度对烟叶理化质量的影响,以及统计学相关和回归方法对出口质量烟叶温度和含水率的稳定性控制研究两个方面,且大多为试验研究,而在利用烟叶松散回潮生产实际大量数据开展数字化建模及预测研究方面还处于空白状态。
贝叶斯网络(Bayesian network)又称信度网络,是贝叶斯方法的扩展,是目前不确定知识表达和推理领域最有效的理论模型之一,适用于表达和分析不确定性和概率性的事件,应用于有条件地依赖多种控制因素的决策,可以从不完全、不精确或不确定的知识或信息中做出推理。目前,贝叶斯网络已成功应用于机器学习[10-11]、人工智能、生物信息学[12]、金融分析[13]与预测[14]等多个领域。试验拟采用贝叶斯网络分析方法,针对某卷烟规格在制丝线松散回潮工序上产生的2018年全年数据,通过建立烟叶松散回潮网络模型,对工艺参数与质量指标之间的复杂关系进行研究与分析,并对该卷烟规格在松散回潮工序上产生的2019年1~3月出料质量数据进行预测与分析,旨在为合理指导卷烟加工生产实际提供依据。
1 数据处理与网络模型构建方法
1.1 数据采集和预处理
在卷烟企业制造执行系统(MES)上,以生产批次为单位采集某卷烟规格在2018年松散回潮工序的生产数据,全年共采集到2 096个批次。其中,采集频次为6 s/个,每批次生产时间约1.5 h,采集工艺参数和出料质量指标共10项。
采集的数据往往包含无用、缺失、异常等无效数据,需对其进行必要的筛选、剔除、修整等预处理。数据预处理流程如图1所示,主要包括无用数据剔除、非稳态数据剔除、异常数据剔除及数据分类存储等步骤。对2018年采集的2 096批烟叶松散回潮生产数据,经数据筛选、剔除、修整等预处理后共得到1 836批有效数据。
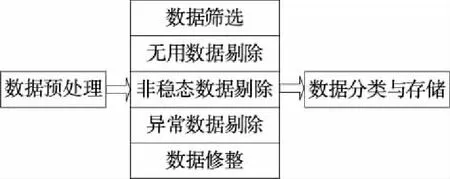
图1 数据预处理流程Figure 1 Flowchart of data preprocessing
1.2 网络模型构建方法
贝叶斯网络模型的理论基础来源于贝叶斯公式:
(1)
式中:
P(A|B)——事件B已发生的条件下事件A的概率,%;
P(B|A)——事件A已发生的条件下事件B的概率,%;
P(A)——事件A发生的概率,%;
P(B)——事件B发生的概率,%。
贝叶斯公式描述了随机变量A和B的关系,提供了基于先验分布信息和观察值的系统状态预测方法。贝叶斯网络构建的方法参照文献[15],其构建基本流程如图2所示,主要包括:① 基于不同属性数据组成复杂网络的节点集合;② 采用协方差方法计算节点间相关性,确定网络路径,构建初步的复杂网络结构;③ 采用最大最小爬山算法,实现复杂网络结构优化;④ 采用最大似然估计法,确定复杂网络参数。
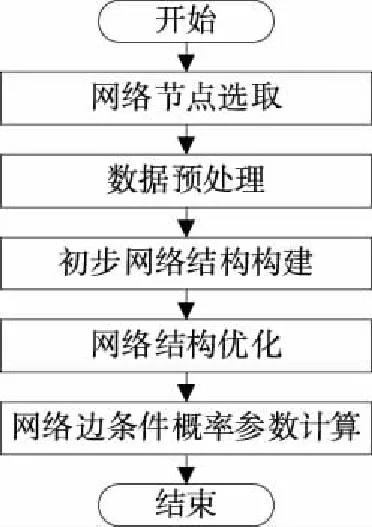
图2 网络模型构建的基本流程Figure 2 Basic flowchart of establishment of Bayesian network model
2 结果与分析
2.1 贝叶斯网络模型构建研究
基于烟叶松散回潮2018年全年的1 836批有效数据,以工艺参数气水混合自动阀门开度、单位时间物料累计量、加水比例、蒸汽自动阀门开度和工艺热风温度为自变量节点,以质量指标出料含水率和出料温度为因变量节点。同时,为确保网络模型构建的合理性,结合松散回潮工序的实际情况,通过添加白名单的方式,约束松散回潮工序复杂网络模型中的工艺参数与质量指标间的路径。运用贝叶斯网络分析方法,建立了工艺参数与出料质量的贝叶斯网络模型,其拓扑结构如图3所示。
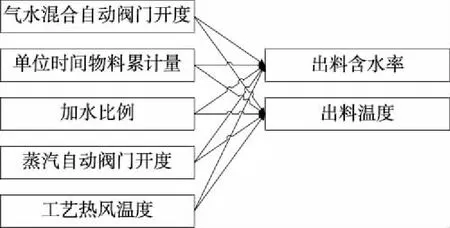
图3 工艺参数与出料质量的贝叶斯网络模型拓扑结构
该模型反映了烟叶松散回潮中工艺参数与质量指标之间的内在关系,为进一步揭示各工艺参数对质量指标的影响,通过提取自变量节点与因变量节点之间的路径参数,得到各工艺参数对出料含水率和出料温度的影响系数和权重,结果见表1。
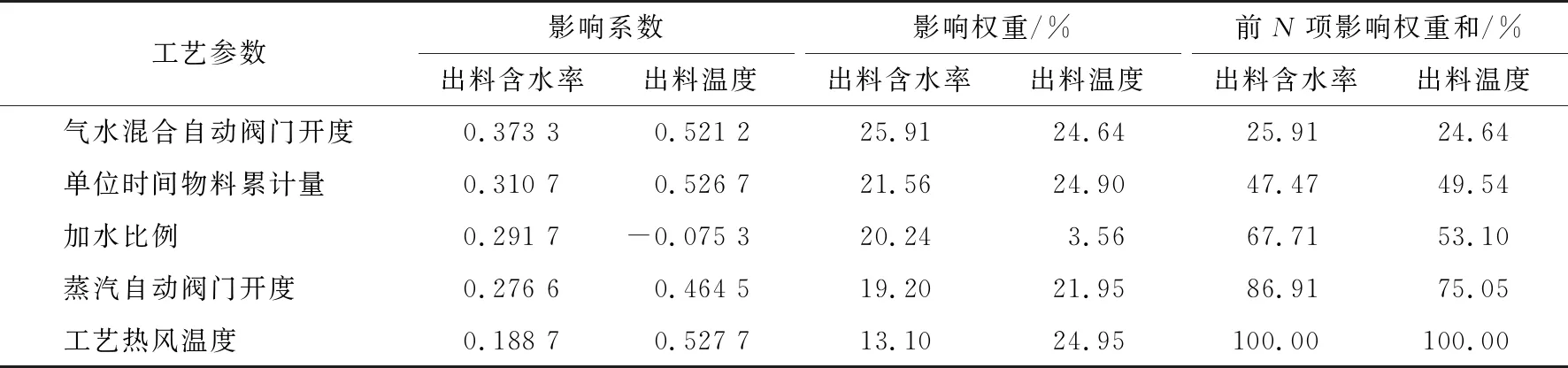
表1 工艺参数对出料含水率和出料温度的影响系数和权重
由表1可知,各工艺参数对出料含水率有一定影响,且均为同向影响(影响系数为正),即出料含水率随各工艺参数的增大而增大,其影响程度依次为气水混合自动阀门开度>单位时间物料累计量>加水比例>蒸汽自动阀门开度>工艺热风温度,影响权重分别为25.91%,21.56%,20.24%,19.20%,13.10%;各工艺参数对出料温度均有一定影响,其中加水比例为反向影响(影响系数为负),其影响程度依次为工艺热风温度>单位时间物料累计量>气水混合自动阀门开度>蒸汽自动阀门开度>加水比例,影响权重分别为24.95%,24.90%,24.64%,21.96%,3.56%;气水混合自动阀门开度和工艺热风温度分别是影响出料含水率和出料温度最为显著的影响因素。因此,基于贝叶斯网络构建的松散回潮工序复杂网络模型,不仅能反映各工艺参数对质量指标的影响规律,还能反映多个工艺参数与质量指标之间的复杂网络关系,进而为工艺参数优化设计、工艺技术标准修订及加工过程质量预测与维护提供指导。
2.2 贝叶斯网络模型预测应用研究
为验证上述工艺参数与出料质量贝叶斯网络模型的有效性和实用性,运用该网络模型,针对该卷烟规格2019年1~3月烟叶松散回潮产生的451批有效数据,已知各工艺参数,预测出料含水率和出料温度,并与真实值进行对比分析,结果见图4、5。
由图4、5可知,基于烟叶松散回潮生产实际的工艺参数数据,采用网络模型对出料含水率和出料温度进行预测,其预测值与生产实际真实值较接近,且变化趋势较一致,说明预测值与真实值吻合较好。
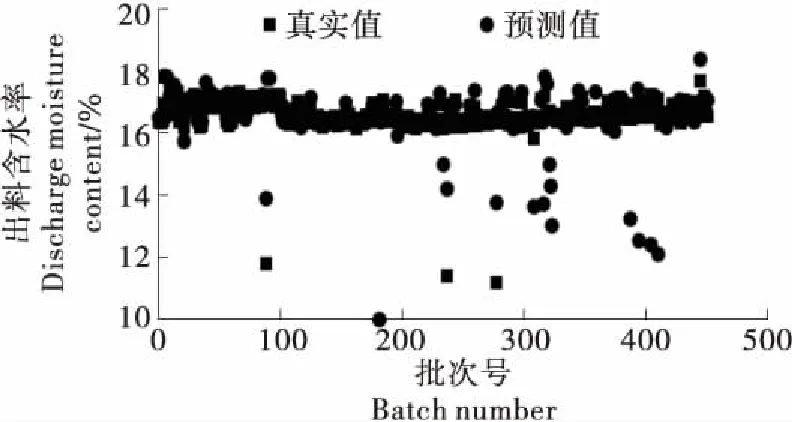
图4 出料含水率预测值与真实值对比
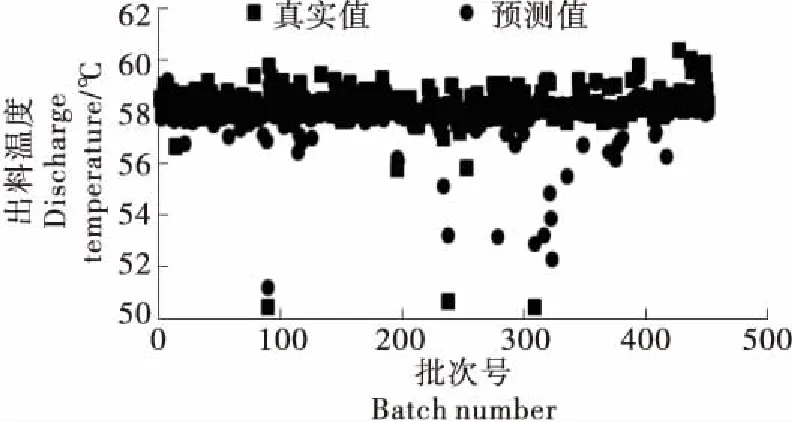
图5 出料温度预测值与真实值对比
为进一步掌握网络模型预测值与真实值的吻合程度,结合烟叶松散回潮工艺技术标准对出料质量的要求,对图4、5的预测值和真实值进行统计分析,其结果见表2。
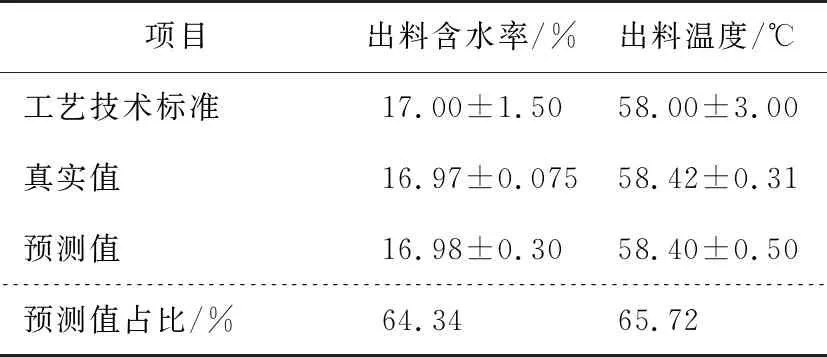
表2 网络模型预测值与真实值统计分析
由表2可知,出料含水率的工艺技术标准要求为(17.0±1.5)%,生产实际值为(16.97±0.075)%,而预测值为(16.98±0.30)%,占64.34%;出料温度的工艺技术标准要求为(58.0±3.0) ℃,生产实际值为(58.42±0.31) ℃,而预测值为(58.40±0.50) ℃,占65.72%;说明预测值具有较好的预测精度和预测效果。
综上,试验构建的工艺参数与出料质量贝叶斯网络模型在预测应用方面拥有较好的精度和效果,具有较好的实用价值和应用前景。
3 结论
基于烟叶松散回潮工艺参数和出料质量数据组成的复杂网络节点集,采用协方差方法计算节点间相关性,确定网络路径,初步构建复杂网络结构,并采用最大最小爬山算法对网络结构进行优化,采用最大似然估计法,确定网络路径参数,构建了工艺参数与出料质量贝叶斯网络模型,并结合松散回潮生产实际情况,通过添加网络结构“白名单(允许)”和“黑名单(禁止)”等约束方式,保证了网络模型构建的合理性。网络模型对出料含水率和出料温度的预测结果表明,构建的网络模型是切实有效的。后续可将网络模型应用于打叶复烤、润叶加料、叶丝干燥、加香等卷烟加工关键工序,辅助工艺技术人员开展过程质量维护、工艺参数设计及工艺标准制修订,对提升卷烟加工工艺水平意义重大。
