社会网络下分配众包任务的真实机制

秦海燕，章永龙，李 斌*

（1.扬州大学广陵学院，江苏扬州 225000；2.扬州大学信息工程学院，江苏扬州 225000）

（*通信作者电子邮箱bl@yzu.edu.cn）

0 引言

在众包中，任务被外包给一组不确定的工人而不是指定雇员。Amazon Mechanical Turk 是一个功能性的众包平台，在这个平台上，任务请求者发布翻译、标记等任务，浏览众包平台的网民能够完成这些小型任务，并且获得少量的报酬。尽管只有小额报酬，兼职或全职雇佣者还是愿意承接不同类型的任务。这不仅比任务请求者线下雇佣员工的成本低，而且有助于提高工作质量。

值得注意的是，很少有关注众包工人之间社会网络的研究。以往的研究中，科学协作网络被认为是一种具有代表性的社会网络，其中团队合作是科学协作的研究要点［1］。有些研究项目过于复杂，由一个科学家完成不了。因此，科学项目的开展必然需要许多科学家的合作，他们能根据自己的研究主题和兴趣形成或建立社区。社会网络为社会工作者之间的合作提供了一个可用的平台。牛津英语词典可以被看作一个大规模的众包任务［2］。可以想象，如果牛津英语词典出版商雇佣的工人彼此熟悉，他们一定会更有效地编纂词典。众包中，TopCoder是一个具有代表性的软件开发众包市场，每个项目都需要一个团队相互合作共同完成。事实上，在众包中考虑工人之间的社会网络，工人、任务请求者和平台都将获利。对工人来说，他们宁愿与熟悉的人合作，也不愿与那些需要进一步磨合的人合作。这样，这项任务就会更出色、更有效地完成。任务请求者也会很高兴接收到更高质量的结果。文献［3］也特别指出了工人完成众包任务过程中质量的重要性。此外，平台可以雇佣更少的工人，从而降低成本。

众包任务按其复杂性可分为复杂任务和简单任务［4］。本文讨论了众包中复杂任务的分配问题，并且众包工人之间存在社会联系。首先，任务请求者将一个必须由多个专业员工完成的任务发布到众包平台上，同时还会提交一个报价，这是任务请求者愿意支付的最高报酬。然后，平台将任务公布在社会网络上。在平台上，具备完成该任务单个或多个技能的工人将申请该任务。接着，平台将执行拍卖策略，将任务分配给某个团队。工人完成任务之后，任务请求者将通过众包平台付款给团队成员。任务请求者最终的支付不能高于自己的报价，也不能低于团队的要价。这种场景下，仍有几个挑战。首先，社会网络中任务分配问题已经被证明是NP 难问题［5］，因此，提出一个计算有效的机制是最重要的问题。除此之外，社会网络中工人之间互连关系是十分复杂的。因此，该机制还应该利用好工人之间的社会联系，找到一个合适的团队来完成任务。最后，自私的工人可能会谎报他们的要价，以获得更高的效用。因此，该机制必须确保是真实的。

针对上述问题，本文提出了一种社会网络下分配众包任务的真实机制（Truthful Mechanism for Crowdsourcing task assignment in Social Network，TMC-SN）。该问题被模拟成一个拍卖，其中任务请求者是买家，工人是卖家，众包平台充当拍卖者。任务请求者发布任务，相连的工人提交技能后，众包平台将进行分配。TMC-SN 提出了一种能在多项式时间内有效分配任务的方法。为了找出最合适的团队，TMC-SN从边际贡献和团队凝聚力两个方面来衡量工人对团队的适应性。与此同时，本文还考虑到了自利的参与者，他们可能为了获得更高的效用而谎报自己的价值。因此，拍卖被成功引入到TMCSN 机制中来防止参与者谎报。TMC-SN 满足拍卖的所有属性，包括真实性、个体理性和预算平衡性。

1 相关工作

任务分配是众包中最重要的过程之一［2］。以任务分配为中心，相关工作可分为两类：1）有或没有拍卖的任务分配；2）有或没有团队合作的任务分配。

1.1 有或没有拍卖的任务分配

空间众包是众包的热点问题之一。在该场景下，Hassan等［6］提出了一种基于组合分式规划方法的距离可靠性比（Distance-Reliability Ratio，DRR）算法和一种扩展算法DRRUCB（DDR based on Upper Confidence Bound），当工人可靠性未知时，该算法利用区间评价启发式算法来近似工人的可靠性。Cheng等［7］针对多技能空间众包问题，提出了三种有效的启发式方法，分别是贪婪、分治和基于成本模型的自适应算法。同样地，文献［8-9］都提出了贪婪算法来近似求解空间众包中任务分配的问题。尽管上述方法能够有效地解决任务分配问题，但是忽略了自私的参与者，他们可能会谎报价值以提高自身效用。TruTeam 算法［10］是众包环境下典型的组建团队来完成众包任务的真实机制。TruTeam 算法采用了关键支付来确保参与者的真实性。因此，引入激励机制来激励并约束工人是必要的。

1.2 有或没有团队合作的任务分配

Yue 等［11］在任务请求者的预算内组建了虚拟团队来完成任务，并声称是最佳匹配。虽然他们提到了团队合作的重要性，但在算法中并没有体现工人之间的团队合作。同样，TruTeam 算法［10］考虑了工人单个技能的边际贡献，但是团队合作被忽略了。Xu等［12］提出了三种众包模式，并且为这三种模式设计了一个真实的任务分配机制，它遵循匹配的方法来解决每一个模型的价值最大化分配问题。他们虽然考虑了任务请求者的偏好和工人工作量的限制，但没有提及团队合作。当完成宏任务时，比如编写文档、设计产品或开发软件，这些任务比微任务需要更多的时间和经验，互助的团队合作也就显得尤为重要［13］。Wang等［14］研究了复杂任务分配，处于社会网络中的工人最终形成团队完成了任务。他们强调最终形成的团队，成员之间的社会网络必须是连通的。因此，要高效地完成任务，团队合作是必须要考虑的。

2 问题描述

2.1 系统模型

任务请求者：任务请求者可以在平台上发布任务R，以及任务R的报价b。b是任务R被成功完成后的预估价值，可以不等于任务的真实价值b～。假设，任务请求者现需要τ种技能，S={s1，s2，…，sτ}，来完成任务R。是一个τ维的集合，其中表示完成任务R是否需要第k个技能sk。SR′是未被覆盖的技能集合，SR′一开始等同于SR，随着工人加入团队，SR′会更新。

工人：每一个工人ai∈A都会提交一个元组Ci=给平台。在Ci中，表示ai是否具备第k个技能，而是ai贡献技能sk期望的奖励。不一定等于ai贡献技能sk的真实成本。C={C1，C2，…，Cm}是所有工人的竞标信息。考虑到工人之间的社会网络，用Nei(ai)来表示与ai直接相连的工人集合。

对于任务R，工人可以贡献一个或者多个技能。因此，引入总成本oCi的概念来表示工人贡献的总的技能成本。H={h1，h2，…，hτ}代表技能集合S的权重，hk表示贡献技能sk所需付出的工作量。如果ai所具备的技能在SR′中是未被覆盖的状态，ai总成本的计算方式如下：

平台：任务请求者和工人提交相关的信息给平台之后，平台输出拍卖的结果，包括最终完成任务的团队成员T⊆A，团队成员的支付集合P={p1，p2，…，pm}。

任务请求者的效用等于完成任务的真实价值与最终支付给团队的总报酬之差：

同样地，被雇佣的工人ai∈T的效用等于拍卖平台给的报酬与付出的成本之差：

2.2 相关定义

本节介绍几个TMC-SN 预期需要满足的经济属性以及后面将使用的一些概念。

定义1真实性。一个拍卖是真实的，表明不论买家还是卖家都不能通过谎报报价或者要价来获得更高的收益。在TMC-SN 机制中，这表明，对于买家发布任务R，如果b=，UR是最大的；对于卖家∀ai∈A，如果=oCi，Ui是最大的。

真实性是拍卖理论中最重要的属性。既然公开真实的报价或要价能获得最高的效用，理性的买卖双方就不会出现谎报的行为。

Myerson定理［15］是拍卖中重要的理论，具体如下：

定理1Myerson 定理。一个拍卖是真实的，当且仅当同时满足：

单调的分配规则：如果ai报价时被成功分配，那他报价时仍然能被分配。关键支付：关键支付作为ai的最终报酬，如果ai报价高于关键支付，那他就不能在拍卖中获胜。

定义2个人理性。被成功分配的卖家得到的报酬高于其付出的成本，被成功分配的买家支付的金额低于其预算。换句话说，如果交易成功，对于∀ai∈T，pi≥oCi；对于R，。

定义3预算平衡。预算平衡是指任务请求者的预算大于支付给工人的总报酬，即。

定义4社会福利。社会福利是所有成功被分配的买家、卖家和拍卖者的效用之和。社会福利也被认为是被成功分配的买方总价值和被成功分配卖方总成本之间的差额。

定义5计算有效性。当且仅当算法可以在多项式时间内执行时，该算法才是计算有效性的。

3 TMC-SN机制设计

3.1 详细设计

一个团队的表现会受多方面因素的影响。首先，任务请求者更偏爱贡献力更大的员工。其次，文献［16］指出，群体凝聚力与团队的绩效正相关。团队越熟悉，相互之间磨合得越好，完成任务的质量也就越高。因此，综合考虑工人的贡献和工人之间的团队凝聚力，给出如下定义：

定义6边际贡献。如果ai被选中进入团队T，ai的边际贡献的值是ai对于未覆盖的技能集合SR′所贡献的工作量，即

定义7团队凝聚力。如果ai被选中进入团队T，团队凝聚力的值是ai与团队成员之间通信成本之和，即

定义8工人的适宜度。工人的适宜度与边际贡献和团队凝聚力有关。因此，ai的适宜度fitness(ai)定义为：

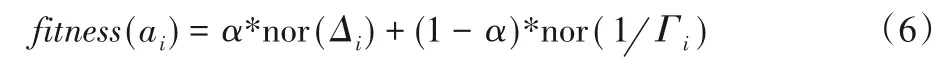
其中：α∈[0，1]是边际贡献与团队凝聚力之间的调节参数；nor(·)是归一化函数。

TMC-SN 机制如算法1 所示。在算法开始时，先搜索团队成员的邻居，并将其添加到Neis中。实现分配时，选择单位工人适宜度成本最小的工人ai作为加入团队的候选人，即候选人的在集合Neis中最小。可以肯定的是，候选人与团队成员之间是有边相连的。因为只有ai∈T的邻居节点才可以加入团队。换句话说，团队成员在算法结束时会形成一个连通子图。为了实现关键支付，在ai没有参与的情况下重建团队。这时，从{Neis′T}中选择单位工人适宜度成本最小的工人aj，并且aj与现有的团队成员之间仍然存在直接联系。因此，

重复选择aj，直到预算用完或者全部技能请求都得到满足。迭代过程中，中的最大值会被作为ai的关键支付。此外，如果ai的关键支付低于剩余预算，ai才会被成功分配。迭代的过程中，一旦一个新的成员加入团队，Δi、Γi和SR′将会更新。最后，如果任务R的技能需求被全部满足，交易才是成功的。

算法1 TMC-SN机制。

由算法1分析可得，TMC-SN 机制是计算有效的。从现有团队中选择团队成员邻居的时间复杂度是O(m)；选择单位工人适应度成本最小的工人的时间复杂度是O(m)；定价阶段的时间复杂度是O(mτ)；为了满足所有的技能而进行了迭代，所以总的时间复杂度是O(m2τ)。因此，TMC-SN 机制是计算有效的。

3.2 理论分析

本节用理论证明了TMC-SN 满足真实性、个体理性和预算平衡。

定理2TMC-SN满足真实性。

证明 首先，任务请求者的真实性是显而易见的。任务R不能被成功分配有两种可能性：一种是R请求的技能不能被满足；另一种是预算有限。如果是第一个原因，不论怎样任务都不能被完成。如果一个预算有限的任务请求者想要被成功分配，那该任务请求者必须提高他的报价直至高于团队的总报价。但是，这种情况下，任务请求者的效益肯定是负的。因此，理性的任务请求者不会谎报价格。

工人的分配和支付规则满足Myerson 定理。首先，很显然TMC-SN 的分配规则是单调的。如果ai报价时能成功被分配，他报价时也会成功被选中，这是因为ai单位适宜度的成本更小。

其次，ai的支付是通过选择一个没有ai参与的团队来决定的。从集合Neis{T∪ai}选出aj，并且aj单位工人适应度的成本在该集合中是最小的。因此，可以得到式（7）。在的情况下，aj将会被选中，而不是ai。在这次迭代中，ai的报酬暂定为。

这时，pi′不是ai的关键支付，因为在Neis{T∪ai}中的竞争者没有被全部考虑，并且任务R的技能请求没有完全被满足。因此，继续迭代直到所有的技能都被满足，或者预算被耗尽。最终ai的报酬pi为关键支付。

在这种支付规则下，如果ai报价高于pi，ai将被放置在最后被选中的工人的后面，最终ai将不会被选中。

综合考虑单调的分配规则和关键支付，工人的真实性得证。

定理3TMC-SN满足个体理性。

证明 对于任务请求者，每次新加入工人到团队之前都会核查b≥pi是否成立，并且每次成功加入新成员之后预算都会更新。换句话说，剩余预算总高于新加入成员的报酬。因此，UR=b-≥0成立。

对于工人，由式（7）可得oCi≤pi，由此可得Ui=pi-oCi≥0。

综上，TMC-SN满足个体理性。

定理4TMC-SN满足预算平衡。

证明 根据支付规则，每次新加入一个工人之前，剩余预算都会被核算是否足够支付该工人的报酬。因此，有b-≥0，即预算高于团队的总报酬。因此，TMC-SN 满足预算平衡。

4 性能评估

本章模拟了众包平台，并且工人们处于一个社会网络中。实验进一步验证了TMC-SN 满足真实性；还观察到调节参数α对交易数、团队凝聚力、效用和社会福利的影响；并且，从交易数、效用、社会福利和成功率等方面，将TMC-SN 机制与不考虑社会网络的TruTeam机制［10］进行了比较。

4.1 参数设置

工人数量m从10 变化到100，默认值为50。任务请求者的报价随机分布在（0.5，6.5］上。工人对单一技能的要价在区间（0，1］中随机取值。如果E(ai，aj)=1，则D(ai，aj)在区间［2，12］内变化。假设任务请求者最多请求6 种技能。调节参数α分布在间隔［0，1］中，默认值为0.5。图示中的某些数据是1 000个独立实例的平均结果。在每个实例中，只有一个任务请求者发布一个任务。

4.2 真实性

在任务请求者和工人中随机选择一个赢家和一个输家，然后在他们报价和要价变化时计算效用。如图1（a）所示，一个成功被分配的任务请求者若以b==4.57 真实报价，获得的效用是2.13。当该任务请求者试图降低他的报价以获得更高的效用时，他将变成失败者并且效用为0。图1（a）中失败的任务请求者的情况表明，当一个原本失败的任务请求者想提高报价赢得拍卖时，他获得的效用将从0 变为负数。图1（b）表明，当一个获胜的工人要价oCi==0.156 时，获得的报酬是0.679，效用为0.523。当工人想通过提高要价来增加效用时，效用在开始时保持在0.523。然而，当他的要价变为0.61 时，他将成为一个失败者，效用为0。图1（b）还表明，当一个失败的工人要价oCi==0.535 时，工人未被成功分配，效用为0。如果他将要价降低到0.195，他将以负效用-0.081 赢得拍卖。换而言之，任务请求者或工人不能通过谎报他们的报价或要价而获益。

图1 TMC-SN真实性验证Fig.1 Verification of TMC-SN truthfulness

4.3 调节参数α对性能的影响

在TMC-SN 机制中，工人对任务的适宜度综合考虑了边际贡献和团队凝聚力。其中，α是这两个因素的调节参数，因此，α对TMC-SN机制的性能有一定的影响。实验数据中的交易数是指1 000 个独立实例中成功交易的数量。图2（a）显示交易数随α的增大而增加。当α增大时，边际贡献在工人适宜度中的重要性增加，相应地，团队凝聚力的重要性降低。因此，对团队凝聚力的关注会降低交易数。图2（a）还可以看出，当α增加时，团队凝聚力先增加，在α=0.4 左右达到最低点，然后波动上涨。团队凝聚力的值是团队通信成本之和。也就是，α越小，通信成本越小，工人之间的联系也就越紧密。图2（b）表明，随着α的增加，任务请求者的效用增加，而工人的效用却减少了。这是因为α越大，交易成功率会提高，任务请求者被成功分配的概率也就会提高，获得的效用相应地提高，而工人却因此获得了更低的效用。图2（c）中，可以观察到，当α增加时，社会福利将减少。这意味着对团队凝聚力的关注有利于社会福利的增长。但是，随着更多工人的参与，社会福利会更少。这是因为团队中的工人越多，对预算的分担就越充分，社会福利就会降低。

4.4 TMC-SN与TruTeam对比

本节将TMC-SN 机制与TruTeam 机制［10］进行了比较。在TruTeam 机制中，忽视了工人之间的社会关系。在这种情况下，工人的适宜度只与边际贡献有关，即α=1。从图3（a）可以看出，随着工人数量的增加，TruTeam 的交易数总是高于TMC-SN。这是因为TMC-SN 考虑了工人的团队凝聚力，交易的限制更严格，成交率就更低。图3（b）表明，任务请求者的效用随着工人的增加而提高，而工人的效用则降低。另外，TruTeam 中任务请求者的效用优于TMC-SN，而工人的效用低于TMC-SN。这表明关注团队凝聚力的对工人是有利的，但对任务请求者是不利的。图3（c）可看出TMC-SN 和TruTeam 的社会福利是波动的。然而，从整体上看，TMC-SN 的社会福利优于TruTeam。对团队凝聚力的关注有利于提高社会福利。

此外，还比较了TMC-SN与TruTeam 的成功率。成功率是指团队完成任务的概率。如果ai和aj相连，则在区间（70%，100%）中随机选择两者共同完成任务的成功率；如果不相连，则在间隔（40%，70%）中随机选择两者的成功率。显然，如果两个工人相连，成功完成任务的几率大于不相连的情况。图3（d）中所示的数据是所有团队成员之间成功率的乘积。结果表明，随着工人数量的增加，成功率降低，但TMC-SN 的成功率始终高于TruTeam。显然，对团队凝聚力的关注提高了任务完成的可能性。

图2 调节参数α对性能的影响Fig.2 Influence of α on performance

图3 TMC-SN与TruTeam的比较Fig.3 Comparison of TMC-SN and TruTeam

5 结语

本文将社会网络下众包任务分配的问题模拟成一个拍卖，其中任务请求者是买家，工人是卖家，众包平台充当拍卖者，并提出TMC-SN 机制以解决该模型下的一些挑战。为了找出最合适的团队，TMC-SN从边际贡献和团队凝聚力两个方面来衡量工人对团队的适应性。理论分析证明TMC-SN 满足真实性、个体理性和预算平衡。在性能分析阶段，进一步验证了TMC-SN 满足真实性，还观察了调节参数α对性能的影响，并比较了TMC-SN 和TruTeam 的性能。实验结果表明，TMCSN机制在社会福利方面具有优势，并且对工人有利。