对PICO算法基于可分性的积分攻击

刘宗甫，袁 征，赵晨曦，朱 亮

（1.北京电子科技学院密码科学与技术系，北京 100070；2.西安电子科技大学通信工程学院，西安 710071）

（*通信作者电子邮箱zyuan@tsinghua.edu.cn）

0 引言

轻量级分组密码以实现效率高、加密速度快、软硬件占用资源少而成为最近几年密码领域的研究热点，在计算能力有限，资源受限的环境下被广泛地应用，其中近些年的轻量级分组密码有GIFT［1］、Midori［2］、LED［3］、SKINNY［4］等。因此，对分组密码的安全性分析成为了密码学研究的重要方向之一。

积分分析在2002 年FSE（Fast Software Encryption）会议上被提出，作为与差分分析相对应的一种分析方法，它对某些结构和算法的分析有时比差分和线性分析更有效。积分分析结合了Square 攻击［5］、Multiset攻击［6］和Saturation 攻击［7］的思想，主要是考虑特定输入对应密文某些位置的零和性质，早期主要局限于以字节为单位的密码算法。2008 年的FSE 会议上，Z’aba 等［8］提出了基于比特模式的积分攻击。2015 年欧洲密码会议上，Todo［9］提出了可分性的概念，来描述介于“活跃”和“零和”之间的隐含性质。在之后的美洲密码会议上，Todo 提出将可分性与S 盒的代数标准型进行结合，可分性将发挥更大的优势。基于这一猜想，Todo 首次给出了MISTY1 算法［10］的全轮破解。比特级可分性质作为可分性的一种特殊情况，可以对算法结构在比特级进行更加精准的刻画。可分性质刚提出来时，由于复杂度的限制，无法在大分组、长轮数算法中应用。为了解决这一问题，2016 年亚洲密码会议上，Xing等［11］把追踪可分性的问题转化为基于混合整数线性规划的问题，调用已有的求解器进行基于比特级可分性的自动化搜索，基于混合整数线性规划（Mixed-Integer Linear Programming，MILP）的方法在一定程度上解决复杂度的问题。随后，该方法在积分分析方面得到了广泛应用［12-14］，并取得了显著成效。

对于PICO 算法，马楚焱等［15-16］利用MILP 方法构造了7轮多维零相关线性区分器，并对10 轮PICO 算法进行密钥恢复攻击，但目前为止尚没有该算法在积分分析下的安全性评估结果。本文采用MILP 搜索工具对PICO 算法进行积分区分器的搜索，搜索得到了轮数最长的10 轮积分区分器，但由于输入活跃比特数太多，可利用的明文数太少，不利于密钥恢复。本文选择搜索到的9 轮积分区分器向后攻击两轮，对PICO 算法进行11 轮的积分攻击。根据现有研究，这是目前为止首次评估PICO 算法在积分攻击方面的安全性。同时，近年来对于密码分析方法之间联系的研究也得到了越来越多的关注，Bogdanov 等［17］研究了零相关线性分析和积分分析之间的联系，并从理论上证明了零相关线性区分器可以和积分区分器相互转化。

1 PICO算法

1.1 PICO算法加密过程

PICO 算法是2016 年Bansod 等［18］设计的混淆扩散网络（Substitution Permutation Network，SPN）结构的超轻量级分组密码，它采用64 比特明文，128 比特主密钥，共迭代32 轮，在每一轮轮函数中将64比特明文和64比特轮密钥逐位异或，然后进行列替换和比特置换操作，具体结构如图1 所示。算法的64 比特明文被排列成4 行16 列的二维数组形式，具体形式可以用矩阵P来表示，其中第i行第j列的元素记为pi，j。

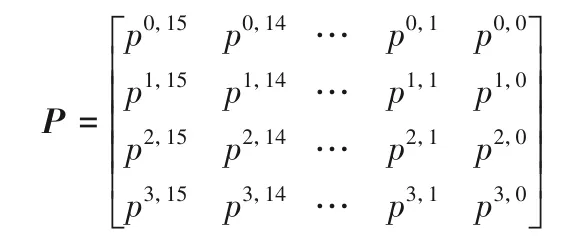
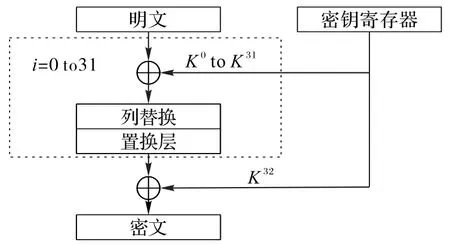
图1 PICO算法结构Fig.1 Structure of PICO

PICO算法的每一轮包含以下3个步骤：密钥加、列替换和置换层，在最后一轮仅有轮密钥加。

1）密钥加：64 比特中间状态矩阵P和64 比特轮密钥的对应位置进行异或操作。

P→P⊕Ki

2）列替换：对状态矩阵的每一列进行S 盒操作，当一个S盒的列输入为C(i)=p3，i||p2，i||p1，i||p0，i时，经过S 盒的输出为S(C(i))=q3，i||q2，i||q1，i||q0，i，其中0 ≤i≤15。PICO 算法S 盒如表1所示。

表1 PICO的S盒Tab.1 S-box of PICO

PICO 算法的非线性层由16 个相同的S 盒并置而成，当S盒的输入为x=(x3，x2，x1，x0)，输出为y=(y3，y2，y1，y0)时，S盒的代数表达式为：

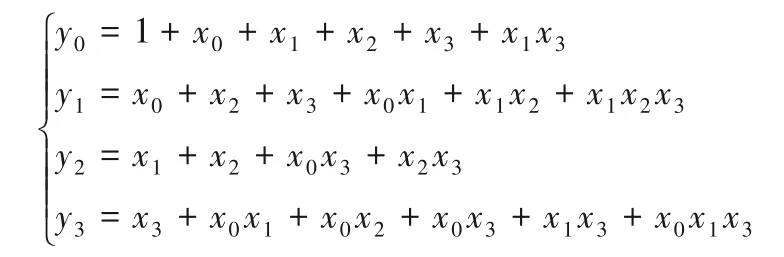
3）置换层：PICO算法通过64比特置换表将状态矩阵的第i行第j列的元素pi，j移动到表2 中对应的位置上，例如BP(p0，0)→p0，10，其中置换表如表2所示。

表2 PICO的P盒Tab.2 P-box of PICO

1.2 PICO算法的密钥扩展方案

PICO 的密钥规模为128 比特，密钥扩展的设计与SPECK算法类似，主密钥Key=k127k126…k1k0存储在密钥寄存器中，首先提取子密钥K0和L1，扩展算法可以表示为：

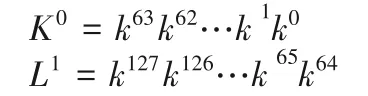
在得到K0和L1后，子密钥K1到K32的生成过程如下：

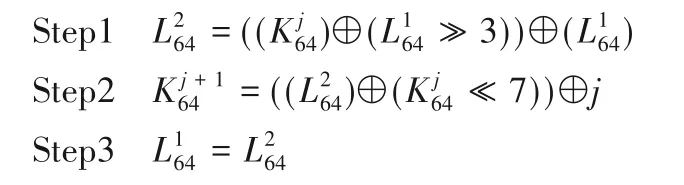
其中j从0 到31 遍历。重复Step1～Step3，便得到了32 轮的全部轮密钥。

2 基于比特可分性质的MILP建模

2.1 基于比特的可分性质

比特乘积函数πu(x)和πU(X)：对于任意，πu(x)是满足u[i]=1的所有x[i]的与，定义为：

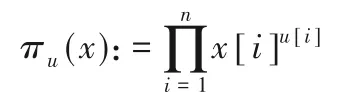
令πU(X)是一个到F2的函数，对于任意的，关于输入的比特乘积函数πU(X)为：

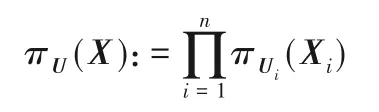
定义1可分性［9］。记X为空间上的多重集，如果集合X满足下面的条件称X具有可分性：

其中：k表示一个m维向量；K表示m维向量集合（第i个元素取0 到li之间的值）。进一步，当考虑比特可分性时，l0，l1，…，lm-1全被限制为1，可分性质可表示为。

定义2可分路径［11］。令输入多重集满足可分性，通过i轮加密后，其中间状态满足可分性，那么可分性质的传递路径为：

{k}≜K0→K1→…→Kr

对于任意的向量ki∈Ki(i≥1)，必定存在向量ki-1∈Ki-1使得ki-1能够传递到ki，其中i∈{0，1，…，r}，则存在一条r轮的可分路径(k0，k1，…，kr)。

2.2 比特可分性的MILP模型

基于MILP 搜索比特可分性的核心思想在于将可分性的传递规则转化为一系列线性不等式，通过构建目标函数将积分区分器搜索问题转化为MILP 求解问题。下面通过线性不等式对三种基本运算（复制、异或、与）和S盒模型进行描述。

1）模型1（复制）。假设用(a) →(b0，b1)来表示复制操作的一条可分路径，下面的等式能够有效地描述可分性的传递规则：

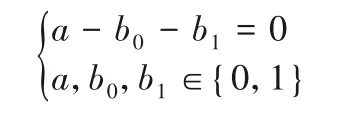
2）模型2（异或）。假设用(a0，a1) →(b)来表示异或操作的一条可分路径，下面的等式能够有效地描述可分性的传递规则：

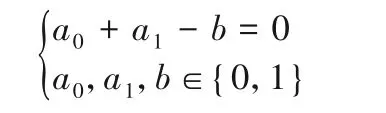
3）模型3（与）。假设用(a0，a1) →b来表示与操作的一条可分路径，下面的不等式能够有效地描述可分性的传递规则：

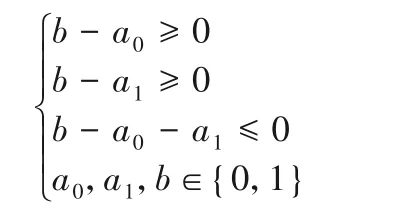
4）S盒模型。为了得到S盒的线性不等式组，首先利用文献［11］提到的算法2 得到一个可分路径的完整列表，接下来调用SageMath 软件生成刻画S盒的线性不等式集合。通常这个不等式集合规模很大，直接调用Gurobi求解器会使得MILP问题在计算上不可解。为了能够降低计算的复杂度，Sun等［19］提出了贪婪算法（文献［19］中的算法1），调用该算法对S盒的线性不等式集合进行化简，能够显著地降低了S 盒不等式的数量。

对于基于复制、异或、与这三种基本操作和S 盒的算法，能够构建线性不等式集合来刻画一轮可分性的传递规律。把这种过程迭代r次，将得到一个线性不等式系统来描述r轮可分性质，该系统的所有可行解对应所有r轮可分路径。

初始条件和终止规则：

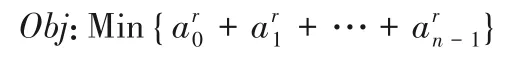
通过设置限制条件L和目标函数Obj便得到了一个完整的MILP 模型，令表示i轮加密后的输出可分性质，当Kr+1首次包含所有n个单位向量，可分性质停止传递，由搜索得到一个r轮的积分区分器。

3 PICO算法的建模过程

3.1 比特可分性的MILP模型

PICO 算法采用SPN 结构，轮密钥加操作并不影响可分性质的传递，因此不将其考量在本文的分析当中。首先应用S盒传递规则，计算得到通过每个S 盒的49 条可分路径，如表3所示。

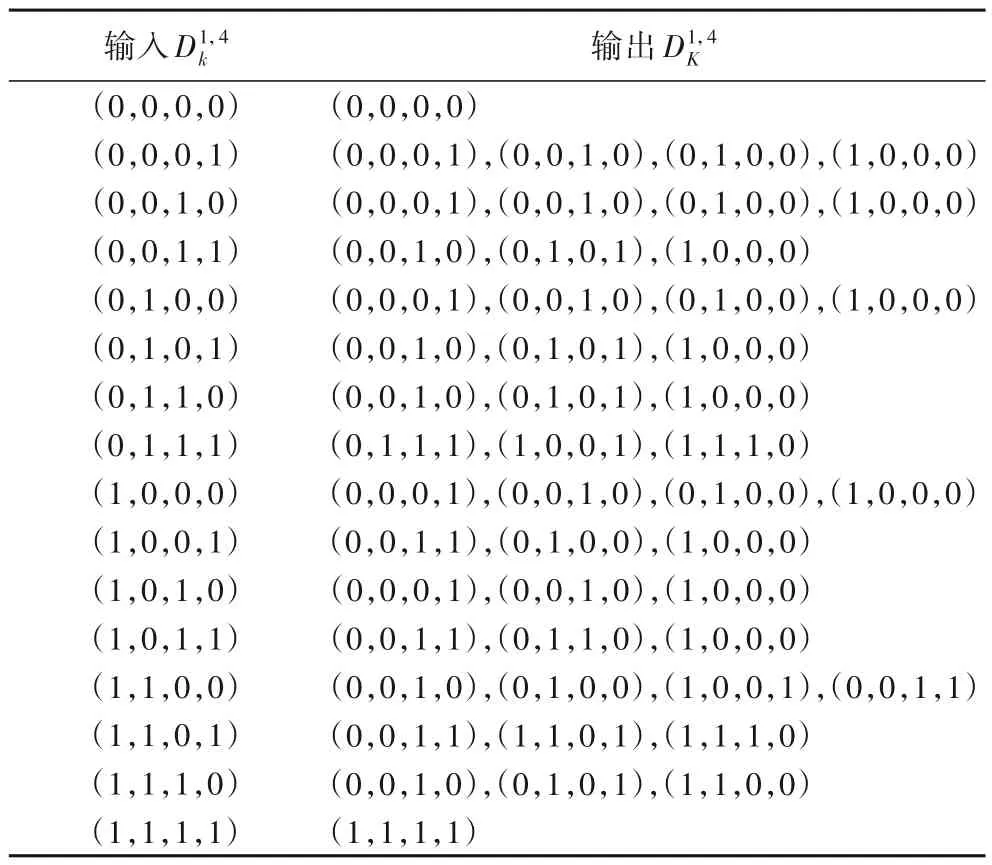
表3 PICO S盒的可分路径Tab.3 Division paths of PICO S-box

其中(a3，a2，a1，a0) →(b3，b2，b1，b0)表示一条可分路径，这49 条可分路径形成了一个点集，并将点集输入到SageMath软件中的inequality_generator（）函数中，将返回52个线性不等式集合，再利用贪婪算法化简得到约束每个S 盒的15 个线性不等式组L，表示如下：

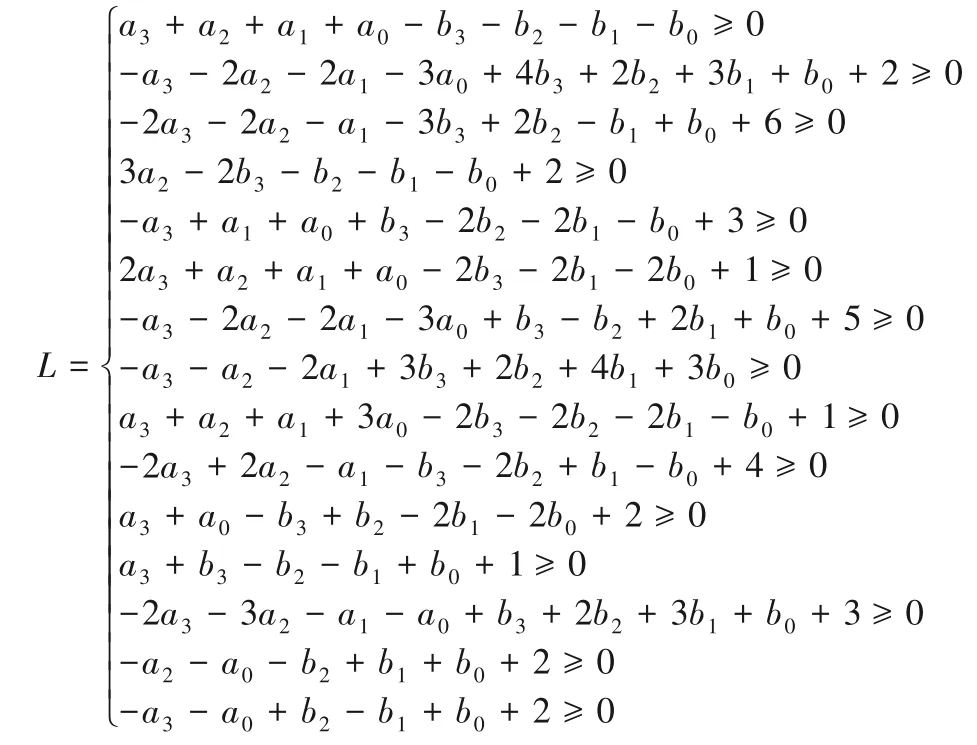
因此PICO 算法的非线性层可用15× 16=240 个线性不等式表示。

PICO算法的线性层通过64比特置换表进行比特移位，因此只需在下一轮可分性质传递过程中改变向量系数的位置。有了描述S 层和线性层的不等式组，便得到了一轮PICO 算法可分性传递的不等式组。迭代r轮之后，便可构造r轮具有可分性路径的线性不等式组，将其作为MILP 模型的限制条件。只要给定初始可分性，便可求解该MILP模型是否存在积分区分器。

3.2 PICO算法的积分区分器

本节根据3.1 节建立的PICO 算法的MILP 模型，采用python 编程建模求解，首次给出了PICO 算法的两个积分区分器。首先根据活跃比特数越多、搜索轮数越长的性质，设定活跃比特数为63，通过大量实验搜索得到PICO 算法11 个10 轮积分区分器，这也是目前为止PICO 算法已知最长的积分区分器。但有些区分器平衡比特数太少，区分优势不明显，通过筛选给出了PICO 算法输入63 个活跃比特、输出26 个比特平衡的10 轮积分区分器。假设a 表示活跃，b 表示平衡，c 表示常数，“？”表示未知，目前搜索到PICO 算法最长的10 轮积分区分器输入状态可表示为：

aaaa，aaaa，aaaa，aaaa，aaaa，aaaa，aaaa，aaaa

acaa，aaaa，aaaa，aaaa，aaaa，aaaa，aaaa，aaaa

输出可表示为：

？？？？，b？？？，b？b？，b？b？，b？b？，b？b？，b？？？，b？？？

b？b？，b？b？，？？b？，？？？？，b？b？，b？b？，bbb？，bbb？

但由于10 轮积分区分器输入活跃比特数较多，最多可利用2 组明文，不利于密钥恢复；同时，活跃比特数越多，意味着数据复杂度越大。因此，通过将对应于S盒的连续4位设置为常数值，其余位置设置为活跃，遍历所有的情况，再次搜索得到PICO 算法13个9轮积分区分器。根据平衡比特数越多，区分优势越明显的性质。本文选择如下的9 轮积分区分器，输入60 个活跃比特，输出33 个平衡比特，并根据此区分器对PICO 算法进行11 轮积分攻击。9 轮积分区分器输入状态可表示为：

aaaa，aaaa，aaaa，aaaa，aaaa，aaaa，aaaa，cccc

aaaa，aaaa，aaaa，aaaa，aaaa，aaaa，aaaa，aaaa

输出可表示为：

b？b？，b？？？，b？b？，b？？？，b？b？，b？b？，b？b？，b？b？

bbbb，b？b？，b？b？，b？b？，b？b？，b？b？，bbb？，b？b？

4 PICO算法的密钥恢复攻击

利用3.2 节给出的9 轮积分区分器，向后攻击两轮，对PICO 算法进行11 轮积分攻击。首先，通过选取特定构造9 轮区分器所需要的明文，得到11 轮加密后的密文。然后，以平衡位置所在的列为单位进行筛选。每一次筛选中，需要猜测第11 轮的轮密钥RK11及第10 轮的轮密钥RK10的部分密钥信息，其中已猜测的部分密钥信息在之后的筛选过程中默认已经唯一确定。最后，对密文进行解密恢复出第9 轮的结果，通过验证第9 轮输出的对应位置比特是否平衡来筛选出正确密钥。

平衡位置的选择不同时，对应筛选出RK11和RK10的密钥字（4 比特）也不同。通过16 次筛选后，便可得到平衡位置与第11 轮的轮密钥密钥RK11及第10 轮轮密钥RK10之间的关系，具体如表4所示。

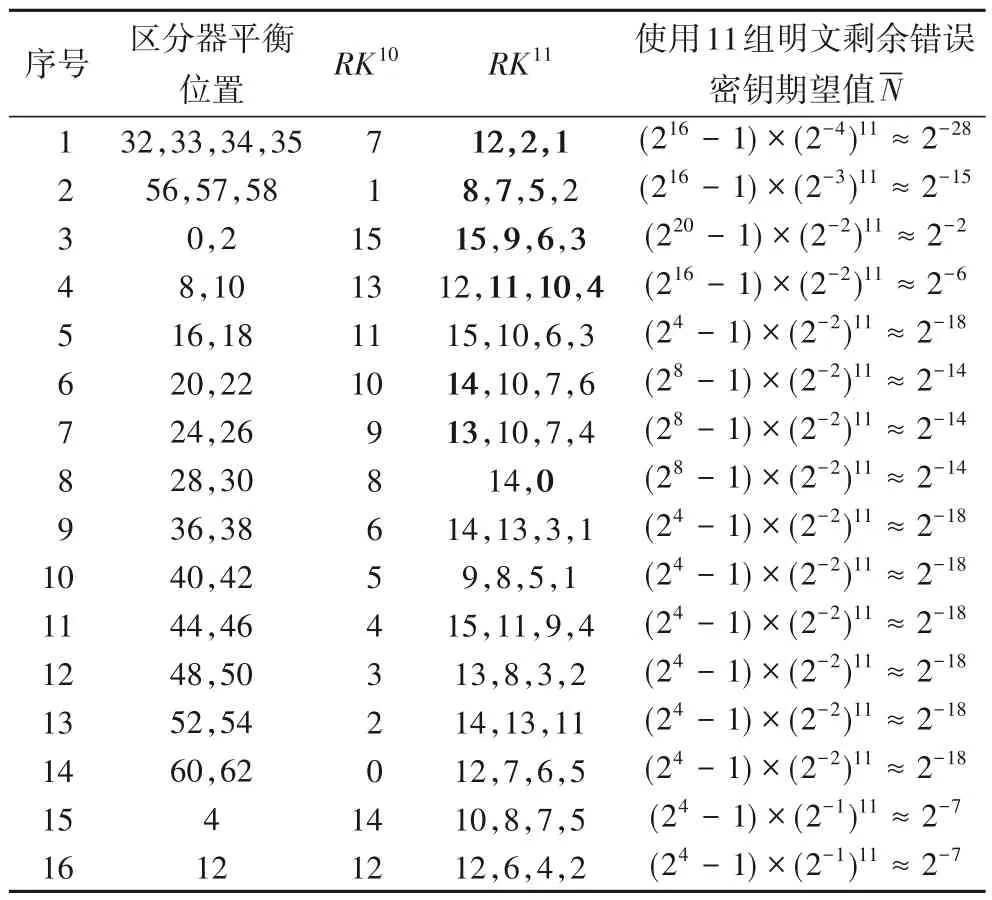
表4 平衡位置与可筛选密钥字的对应关系Tab.4 Relationship between balanced positions and nibbles of recovered round keys

本文选择32、33、34、35 这四个平衡位置为例进行说明，攻击流程如图2 所示。图2 内部结构与1.1 节给出PICO 算法的状态矩阵相对应，该状态矩阵的每一列都可以表示成一个向量，即可以表示成Q15、Q14、…、Q0共16 个向量，其中Qj=(p0，j，p1，j，p2，j，p3，j)T，0 ≤j≤15。下面给出攻击的具体步骤：

Step1 根据输入的初始状态构造9 轮积分区分器，由于输入状态有4 比特为常数比特，因此将p0，8、p1，8、p2，8、p3，8对应位置取定为常数，其余60 个活跃位置遍历{0，1}60，故每组包含260个明文，并对其进行11 轮加密，相应的密文记为C0、C1、…、。

Step2 通过猜测密钥RK11的3 个密钥字共12比特密钥信息，对260个密文进行第11轮解密，计算得到第10 轮的12 比特输出，其中计算表达式为，j∈{1，2，12}。

Step3 计算第10 轮通过S 盒后的中间状态，即Ti=P-1(V(i))，猜测密钥RK10的一个密钥字，计算ti=。

Step5： 选择另一组构造9 轮区分器时的明文，重复Step1～Step4，直到唯一确定。

复杂度分析：表4 利用区分器平衡位置由多到少依次对密钥字进行筛选，即攻击时共需要筛选16 次。RK11已确定的密钥字在表4 中用粗体标注出来，在下次筛选时无需猜测已确定的密钥字。为了唯一确定正确密钥，即保证每一种情况下错误密钥的期望值-N都小于1，因此需要选择11 组明文进行分析。经过16 次筛选后，RK10的16 个子密钥和RK11的16个子密钥共128 比特密钥信息将唯一确定。从而攻击的数据复杂度为11 组(260× 11 ≈263.46)明文，低于明文直接穷举量。每次筛选过程中猜测密钥字的个数不同，其中需猜测5 个密钥字的1 次、4 个密钥字的3 次、2 个密钥字的3 次、1 个密钥字的9 次，所以处理11 组明文整个攻击的时间复杂度共约需263.46×(24×5+3× 24×4+3× 24×2+9 × 24×1)≈283.46次S 盒查表，这相当于283.46/(11× 16) ≈276次11轮加密。此外，为了对猜测的密钥字进行存储，存储复杂度为24×5+3× 24×4+3× 24×2+9 × 24×1≈220。

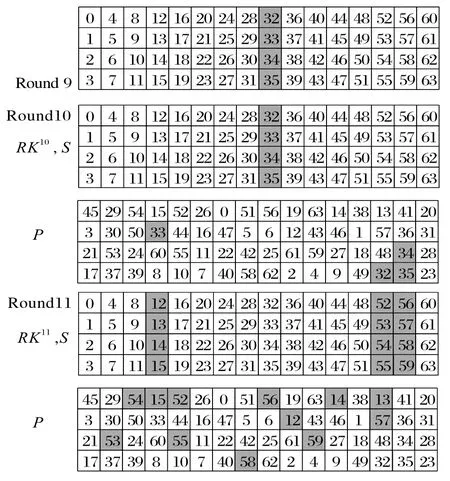
图2 11轮PICO的积分攻击Fig.2 Integral attack on 11-round PICO

下面将本文积分攻击与零相关线性分析方法进行比较，结果如表5所示。

表5 本文方法与零相关攻击方法的实验结果对比Tab.5 Experimental results comparison of proposed method and zero correlation attack method

5 结语

PICO 算法能够很好地抵抗差分攻击［20］、线性攻击［21］、biclique 攻击［22］、零相关攻击［23］和相关密钥攻击［24］，但迄今为止未有人对PICO 算法抵抗积分攻击的能力进行研究。本文主要采用基于比特可分性的MILP 建模方法对PICO 算法进行积分分析，得到了轮数最长的10 轮积分区分器，但由于活跃比特数太多，可利用的明文数太少，不利于密钥恢复。本文选择搜索到的9 轮积分区分器进行11 轮的积分攻击，该攻击经过16 次的筛选能够恢复PICO 算法128 比特密钥信息。其中攻击数据复杂度为263.46，时间复杂度为276次11 轮加密，存储复杂度为220，本文首次给出攻击11 轮PICO 算法的数据复杂度小于穷举攻击的有效攻击。分析结果表明了11 轮PICO 算法不能抵抗积分攻击，但由于在搜索中活跃比特数越多，搜索得到的积分区分器越长，因此使得选择明文的数据量大大增加，如何能够平衡活跃比特数和长轮数之间的关系将是进一步需要解决的问题；同时MILP搜索积分区分器的方法还有一定的局限性，采用文献［11］方法产生的不等式不足以约束大规模的S盒，如8 进8出的S 盒，解决S 盒算法的适应性问题也将是下一步研究的主要方向。