电动变量施肥控制系统的PID参数优化
2020-10-17黄丽萍梁春英王振民于天齐曲云霞
黄丽萍,梁春英,王振民,于天齐,曲云霞
(黑龙江八一农垦大学 电气与信息学院,黑龙江 大庆 163319)
0 引言
我国是农业粮食产量大国,农业的发展除了依靠增大耕地面积和灌溉面积、采用先进的生物技术之外,还需在大量投入肥料的基础上获得[1]。化肥的使用量远远高于粮食的产量,要想提高化肥的利用率,目的在于提高粮食产量和减少环境污染[2]。利用变量施肥技术的应用可以解决这个问题,近些年PID控制常常被广泛应用在变量施肥技术的控制策略研究方面,能够较好地改善控制系统的效果,提高施肥的精度,推动了变量施肥机在国内的智能化发展[3]。然而,由于电动控制系统的非线性与一般PID控制策略的局限性等缺点,导致该控制系统的自适应性能不足。为此,提出了一种智能控制理论,为控制领域的发展提供了新的方法[4]。
在控制领域上中着众多的应用模型,比较常用的是BP神经网络与RBF神经网络这两种人工神经网络模型[5]。BP网络的基本训练算法是一种以梯度为基础的误差下降算法,其原理通俗易懂,但学习速度慢[6];RBF神经网络的作用函数为径向基函数,存在着局限性,对于它的每一个输入输出值,只有少量的权值需要校正,所以网络学习速度明显快于前者[7]。但是,RBF神经网络参数值不好确定,选择不好会导致精度下降。在此基础上,采用遗传算法优化RBF神经网络的参数值,可以提高系统性能[8]。
在学习了解了国内当前的变量施肥基础上,采用直流电机直接驱动的方式,带动排肥轴转动,再由电机转速控制其排肥量。同时,改良PID参数的自适应性方向,探索遗传神经网络PID算法在变量施肥技术中应用的效果,可以提高变量施肥系统的施肥特性,大大减少化肥施用量,提高种植物(大豆)的品质,保护农业生态环境,实现农业可持续发展。
1 电动变量施肥系统
1.1 控制系统组成
电动变量施肥控制系统主要由人机操作界面、电机驱动电路及机具作业的速度采集单元等组成,如图1所示。
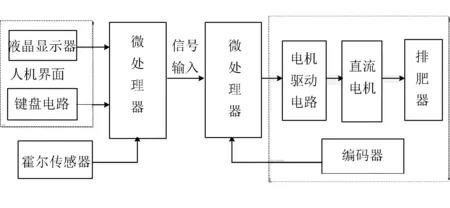
图1 控制系统硬件框图
1.2 工作原理
试验台工作原理:将肥料装入肥料箱后,肥料会因重力的影响而下落到排肥器中。接通电源后,排肥器开始运转,肥料便会落入到排肥器齿轮凹槽中去;电动机带动齿轮转动,通过电动变量施肥的控制系统来调节排肥器的电机转速,通过改变电机的转速控制排肥器的施肥量,肥料会通过排肥口落到试验台上。在试验台的下面有交流减速电机和它配套的调速器,用来提供动力,使螺母在T型丝杆上运动,且使排肥箱在试验台Y轴上运动。因此,可根据肥料箱与试验台之间的相对运动模拟出施肥机机具的地轮和田地之间的相对运动。
2 直流电机数学建模
系统采用ZD1531型号直流电机,用来驱动排肥器运行工作。直流电机的电枢回路的电路方程为
(1)
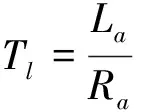
反电动势E与电机角速度ωm成正比,即
(2)
其中,kε为反电势系数;θm为电机轴的转角。
转动轴上的力矩方程为
(3)
其中,km为电机的力矩系数;Ml为负载力矩;Jm为电机电枢的转动惯量。
对式(1)~式(3)进行拉氏变换得
(4)
直流电机的技术参数如表1所示。
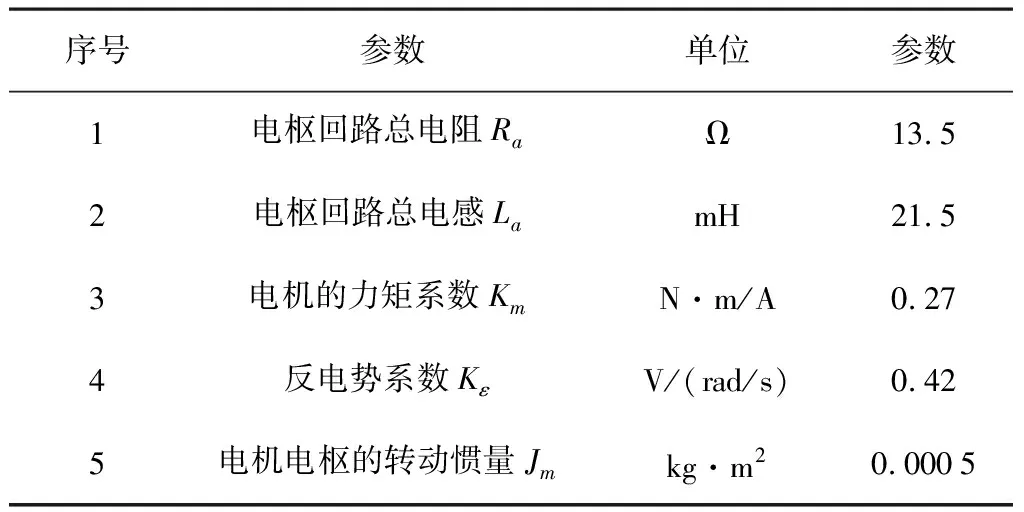
表1 直流电机技术参数
综上所述,可以得到相应的电机数学模型的结构框图,如图2所示。
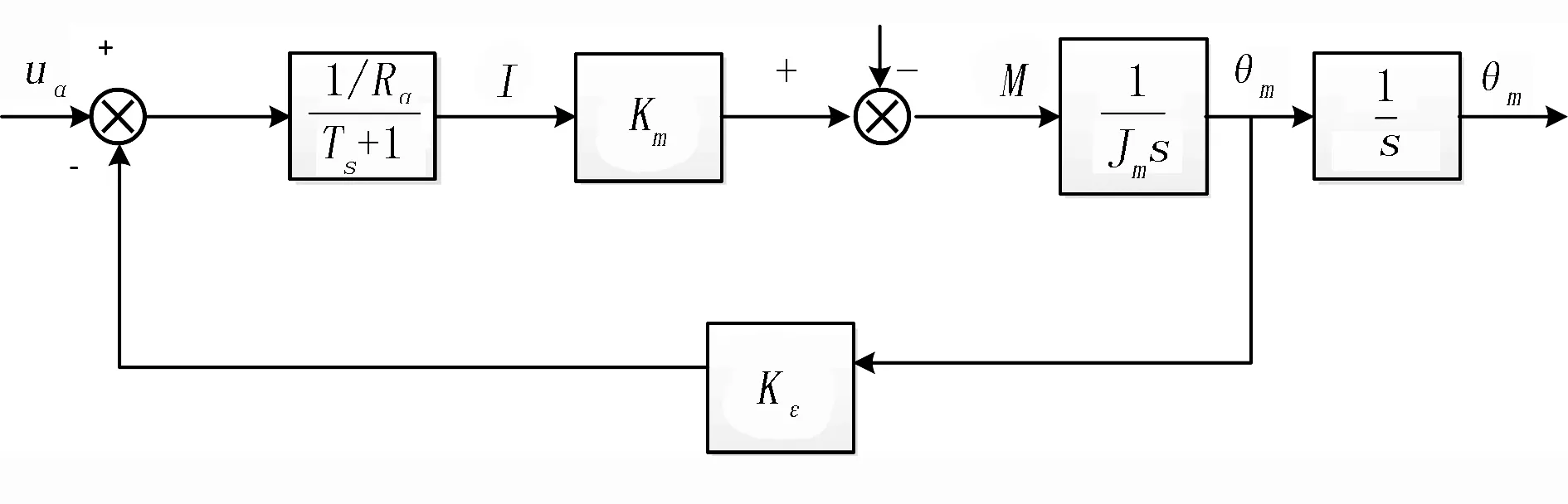
图2 Mathematical model structure diagram of dc motor
3 基于RBF-PID的参数优化
3.1 RBF-PID参数整定原理
基于RBF网络的PID控制器由两个部分组成:
1)经典PID控制器。可以直接控制被控对象,通过采用梯度下降法能够在线调节PID控制器3个参数kp、ki、kd。
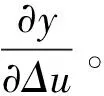
3.2 RBF网络整定PID算法
PID参数整定过程如下:
采用增量式PID算法,控制误差为
e(k)=rin(k)-yout(k)
PID3个输入分别为
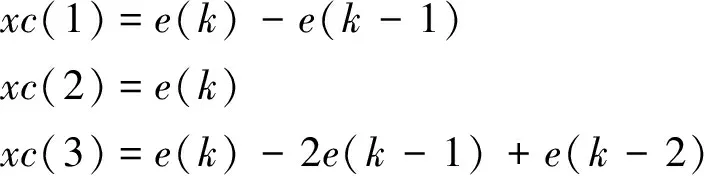
控制算法为
RBF神经网络整定指标为
E(k)=0.5error(k)2
采用梯度下降法分别调整kp、ki、kd,即
(1)
(2)
(3)
3.3 RBF-PID仿真
被控对象是一个二阶传递函数,RBF神经网络结构是一种3层的前向网络。RBF的输入层到输出层是非线性的,隐含层到输出层是线性的,明显加快了其学习速度,同时避免了局部的最小值。其网络输入为Δu(k)、yout(k)、yout(k-1),其输入信号为rin(k)=1.0。通过反复试验,选取学习率为η=0.01、动量因子为α=0.05。通过仿真,得出系统的阶跃响应图如图3所示。
由图3可知:二阶系统的时域性能指标的超调量为σp1=2.37%,峰值时间为tp1=0.09s,调节时间为ts1=0.119s,上升时间为tr2=0.056s,延迟时间为td2=0.004s,振荡次数为N=3。
4 基于遗传算法RBF-PID的参数优化
4.1 遗传算法训练RBF网络
通过遗传算法来训练RBF网络的步骤如下:
1)编码。采用二进制编码,PID的3个参数kp、ki、kd都是采用二进制数表示,构成一个30位的染色体,按照顺序排列依次代表kp、ki、kd参数对应的二进制码。
2)初始群体。一组种群的染色体是遗传算法的开始,染色体要一一对应着即将优化的可变值数组。由此而知,h个隐藏的节点表示染色体,并把径向中心初始化成随机值。
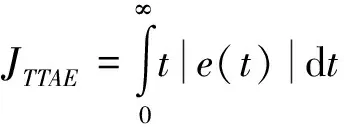
4)选择。根据适应度函数的值,染色体按照降序排列,优胜劣汰,只有最好的染色体才会被保留下来,其他的染色体则会被淘汰。
5)变异。加入变异,使某一位发生变化,其变化是具有一定概率的,存在着引起扰动的可能性,能有效避免发生局部极值的问题。
6)当满足条件时,重复步骤3)~5)。
4.2 遗传算法优化RBF-PID
本系统采用个体数目nind=10,最大遗传代数maxgen=100,变量的二进制位数preci=20,代沟ggap=0.95,交叉概率px=0.7,变异概率pm=0.033。
适应度权值选择为w1=0.99,w2=0.001,w3=2.0。为了使其得到惩罚效果,取w4=100,远远大于其他权值。通过100代进化,得到的优化参数为kp=2.5637,ki=0.2392,kd=0.6917,性能指标J=23.395,优化过程如图4所示。
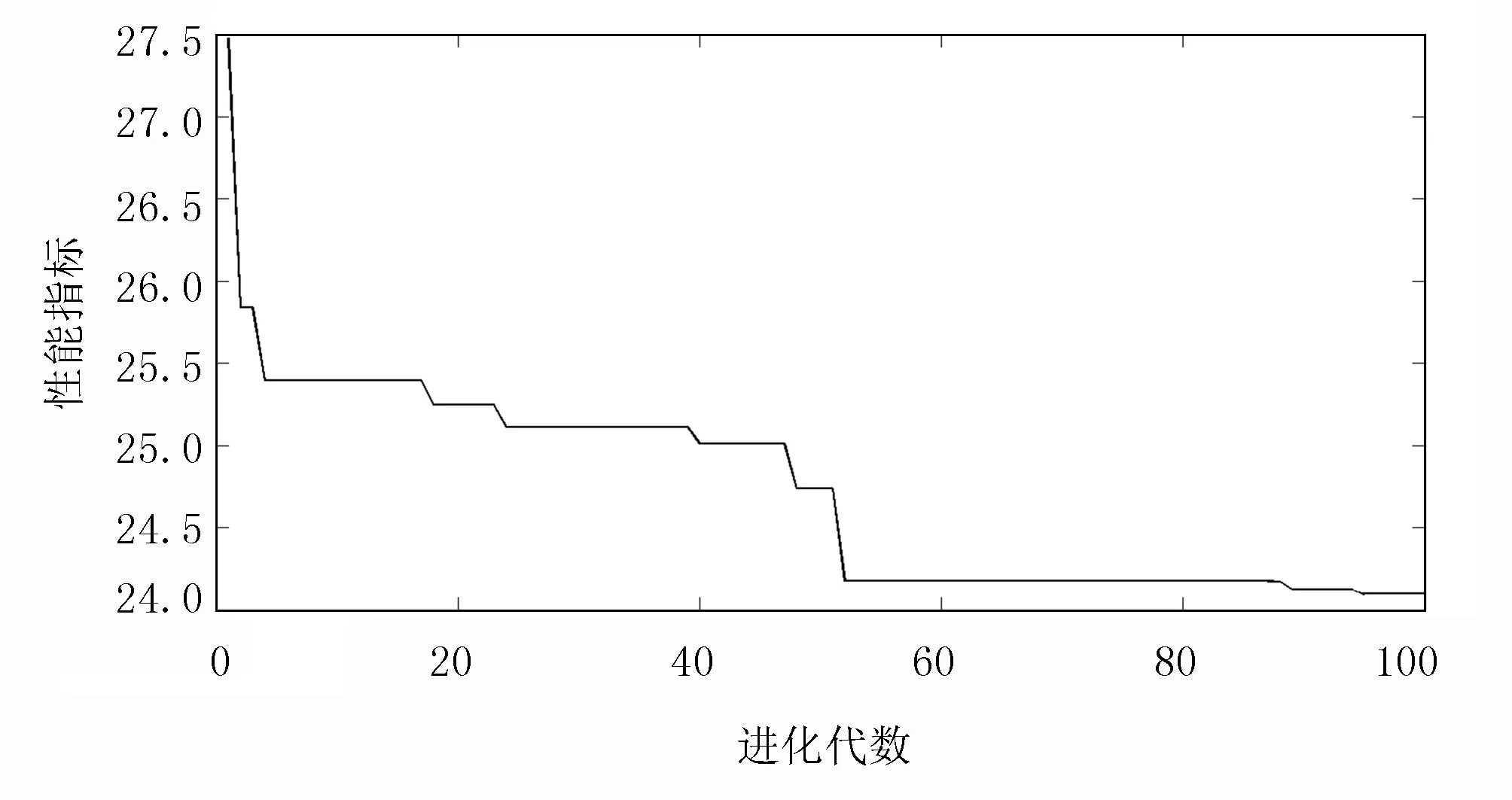
图4 代价函数优化过程
4.3 遗传算法优化RBF-PID仿真
使用MatLab软件对RBF-PID参数自整定进行仿真,RBF网络结构由3个输入向量、6个隐含层神经元及1个输出神经元组成。经过试验,选取RBF网络参数,学习率η=0.01,动量因子α=0.01,其阶跃响应曲线如图5所示。
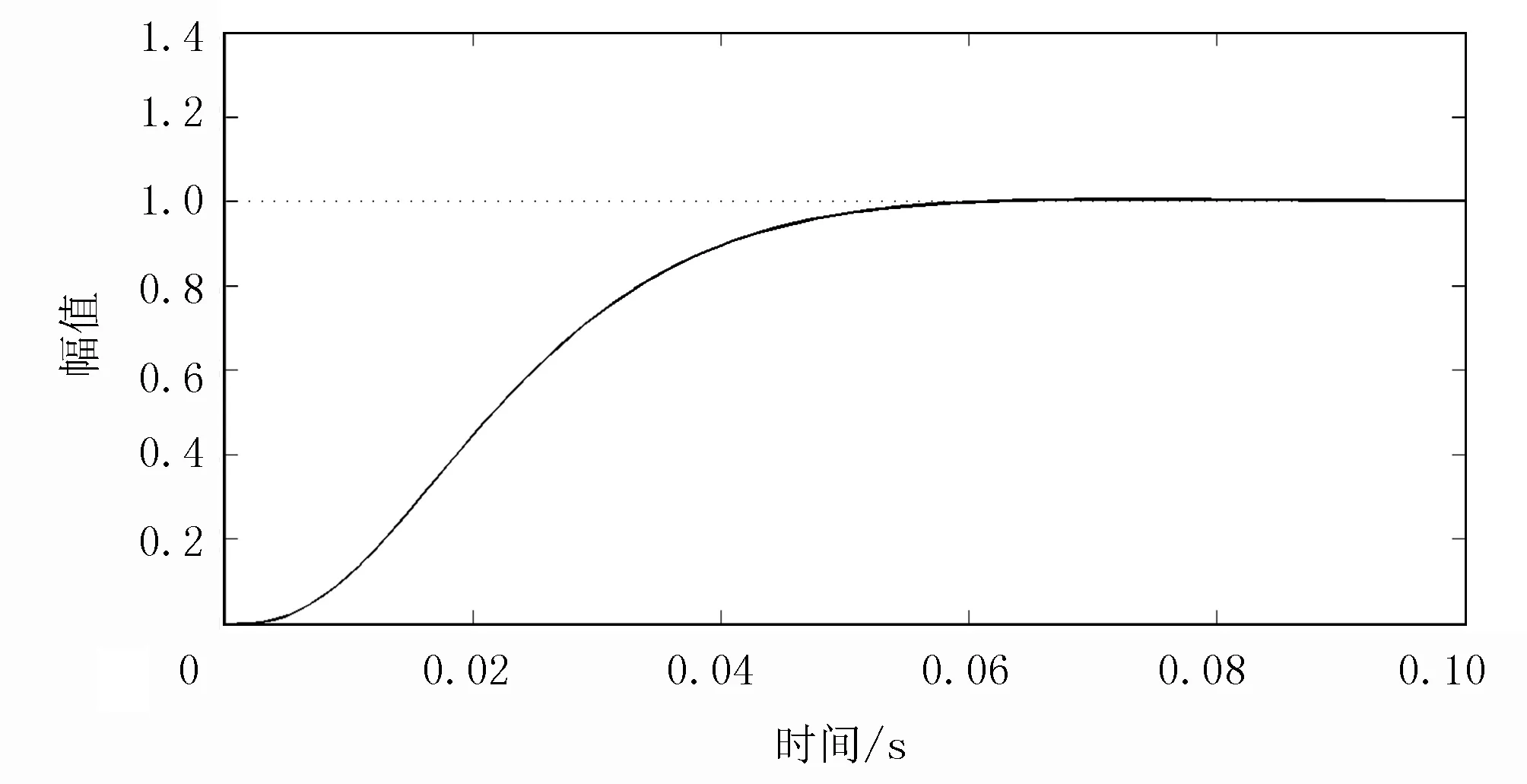
图5 遗传优化RBF-PID阶跃响应曲线
由图5可知:系统的时域性能指标的超调量σp3=0.38%,峰值时间tp3=0.076s,调节时间ts3=0.069s,上升时间tr3=0.054s,延迟时间td3=0.021s,振荡次数N=1。
5 变量施肥试验
5.1 试验条件
1)试验依据:NY/T1003-2006《中华人民共和国农业行业标准-施肥机械质量评价技术规范》。
2)试验时间:2019年4月12日-14日。
3)试验肥料:农用优等尿素。
4)试验地点:黑龙江八一农垦大学电气与信息学院204实验室。
5)试验设备:电子天平、秒表、卷尺。
6)转速范围:70~100r/min,间隔5r/min。
7)初始参数:kp=0.2,ki=0.01,kd=0.2。
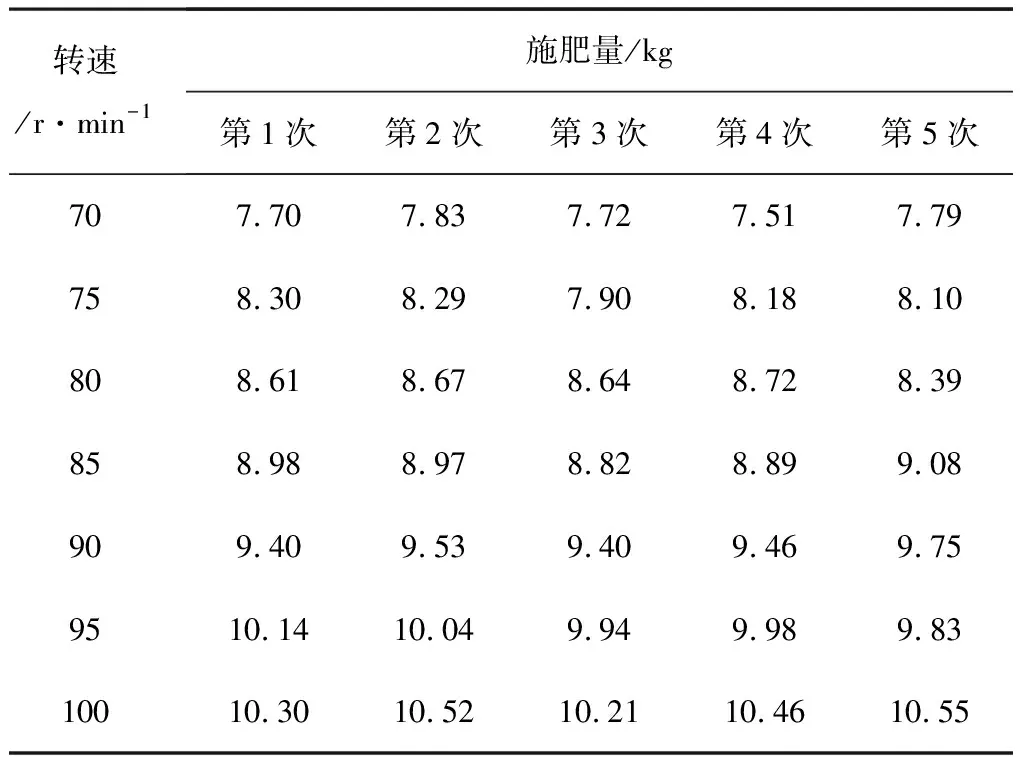
表2 遗传优化RBF-PID算法的电动变量施肥试验数据
5.2 控制特性分析
排肥口试验数据分析如表3所示。
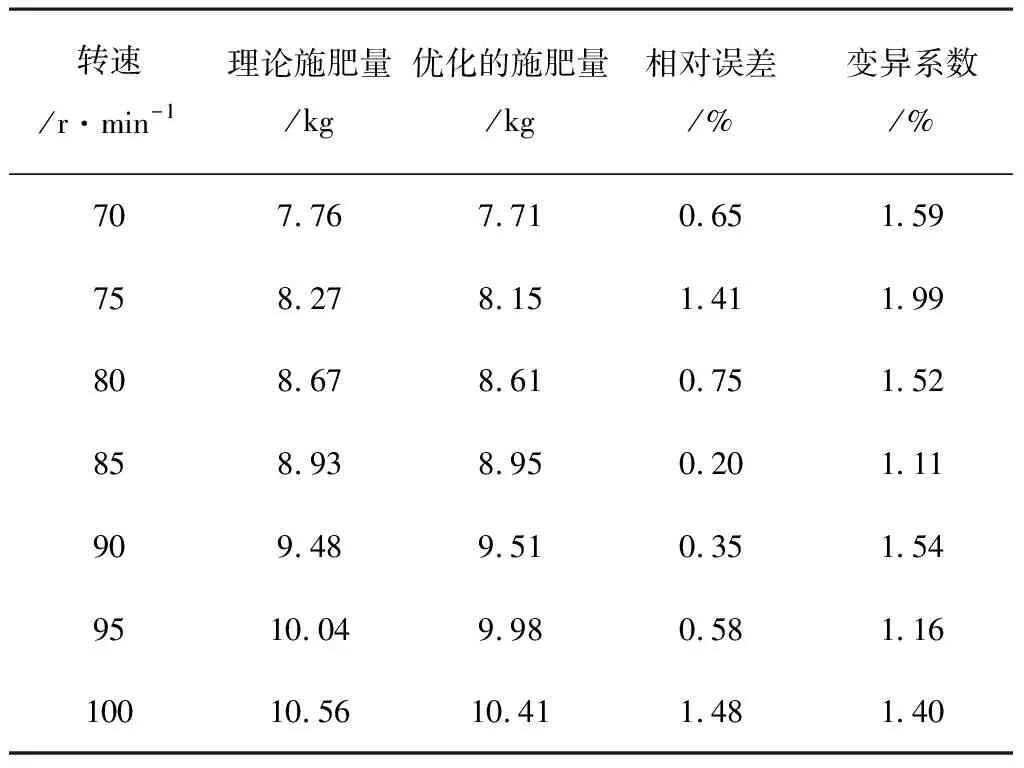
表3 排肥口试验数据分析
6 结论
1)通过仿真得知,遗传算法优化RBF-PID效果最好,减小了系统的超调量,缩短了系统的上升时间,提高了系统的稳定性。同时,控制器参数设定简易,有着良好的自适应能力和鲁棒性的优势。
2)通过试验,由表2、表3可以看出:排肥轴转速在70~100r/min时排肥轴转速与施肥量成正比,施肥量平均相对误差为0.77%,平均变异系数为1.72%,遗传优化RBF-PID算法的电动变量施肥系统具有较高的施肥精度。
