加卸载应力路径对砂岩能量演化机制的影响

2020-10-17郑晓娟王云飞隋智力

硅酸盐通报 2020年9期

郑晓娟，王云飞，隋智力

(1.焦作师范高等专科学校，焦作 454000；2.河南理工大学土木工程学院，焦作 454000； 3.北京城市学院城市建设部，北京 100083)

0 引言

地下工程建设打破了原有的应力平衡状态，开挖卸荷引起工程围岩内部应力调整，这一过程伴随着岩体内部能量的转化，会引起弹性应变能的积累和释放，促进微裂纹的扩展，形成宏观裂隙，造成围岩失稳破坏。因而研究加卸载应力路径下的能量演化特征对分析围岩稳定性具有重要意义。

岩石力学研究者在岩石强度和能量演化方面做了大量研究，如三种砂岩强度特征及强度差异内在原因分析[1]等。从卸荷点、循环加卸载对大理岩和千枚岩变形与破坏能耗的影响研究[2-5]得出，卸荷点与耗散能呈正相关，单位耗散能与损伤比变量呈线性关系。从不同层理角度和含水率下岩石的储能和释放机制研究[6-7]得知，层理方向对千枚岩储能能力影响较大，而对释能机制影响较小。研究了脆性指标和弹性应变能关系[8-9]，并指出脆性指标可由峰值和起裂弹性应变能表示。研究了冲击扰动和动力作用下岩石的能量演化特征，得知单位体积储能随扰动冲击次数增加呈非线性关系变化[10-11]。研究了温度变化[12]、细观结构特征[13]、拉应力状态[14]和岩样再次破碎[15]对岩石能量演化特征的影响。基于能量演化原理建立了能量屈服准则[16-17]。数值分析了岩石尺寸效应和复合煤岩体对能量演化的影响[18-20]。

由以上研究可知，国内外学者在岩石强度和能量演化方面取得了丰硕的成果，但对于同一种岩石在不同应力路径下能量演化的对比分析较少，还需进一步完善。鉴于此，本文以砂岩为例开展了应力路径对能量演化机制、弹性储能极限和能量比例特征影响的研究，可为从能量角度分析地下工程围岩稳定性提供参考。

1 砂岩特性与试验方法

砂岩密度为2 417.76 kg/m3，将砂岩加工成直径50 mm，高度100 mm的圆柱试样，加工精度满足试验标准要求。采用RMT-150岩石力学试验系统进行砂岩单轴、三轴压缩和卸围压试验。单轴压缩选用3个试样，三轴压缩试验围压分别为5 MPa、10 MPa、20 MPa、30 MPa和40 MPa，卸围压试验初始围压分别为10 MPa、20 MPa、30 MPa和40 MPa。试验采用位移控制加载方式轴向加载，加载速率为0.002 mm/s。三轴试验首先以静水压力加载至预定围压，然后伺服控制围压，轴向以0.002 mm/s的速率加载至试样破坏。卸围压试验轴向加载至初始围压对应强度的80%，保持轴向压力不变，分别以1 MPa/s、0.1 MPa/s和0.01 MPa/s三种速率卸除围压至试样破坏。试验加载系统及砂岩试样如图1所示。

图1 RMT-150试验系统与砂岩试样Fig.1 RMT-150 test system and sandstone samples

2 能量计算原理

岩石破坏是能量驱动的结果，其中耗散能使得岩石强度逐渐弱化，裂隙发展贯通，最终导致岩石失稳破坏。在能量分析中取单位体积岩体分析，假设外力功全部转化为弹性应变能和耗散能，则能量转化满足式(1)：

U=Ud+Ue

(1)

式中：U为吸收总能量;Ud为岩石耗散能;Ue为岩石可释放弹性应变能。

图2为岩石应力-应变曲线中能量关系图，阴影部分面积表示加载过程中积蓄的弹性应变能Ue，应力-应变曲线与卸荷弹性模量Eu及横坐标围成的面积为耗散能Ud。在三向应力状态下，具有非线性特征的岩体单位体积能量可按式(2)～式(5)计算。

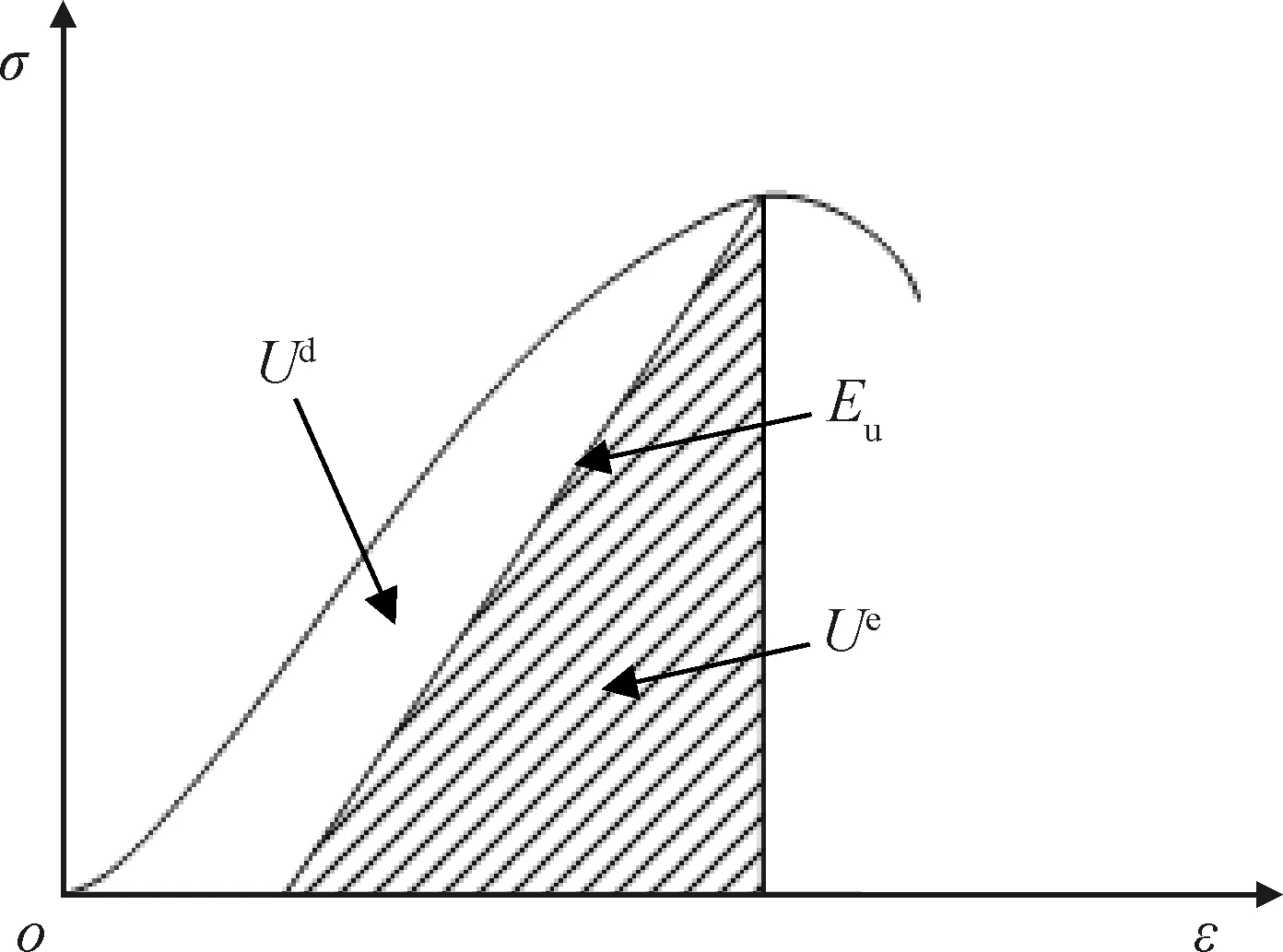
图2 耗散能Ud与可释放应变能Ue的关系Fig.2 Relationship between the dissipation energy Ud and the releasable elastic strain energy Ue

(2)

(3)

(4)

(5)

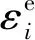
RMT-150岩石力学试验系统本身不具备测试环向变形的功能，在试验过程中无法直接获得环向变形。有的仪器在围压桶中加入环向变形测试装置，但也只能测试岩样一个特定截面变形，实际沿岩样高度的变形并不相同，故其计算仍然带有误差。因此，本文确定环向变形时采用如下估算法：通过砂岩泊松比和轴向变形，反算环向变形来计算能量，尽管这样会带来一些误差，但由于围压相对砂岩破坏轴压都较小，以最大围压40 MPa为例，砂岩破坏时的围压与轴压之比为1/6，加之砂岩破坏变形值本身较小，故其围压负功的估算误差较小。单轴压缩外力功全部转化为岩石吸收的总能量，三轴试验外力功减去围压负功剩余部分为岩石吸收的总能量。

3 能量演化分析

3.1 不同应力路径能量演化特性

根据砂岩应力-应变曲线，按式(1)～式(5)计算获得不同应力路径砂岩吸收总能量、弹性应变能和耗散能随应变的变化规律，如图3～图5所示。图3～图5为部分试验能量演化曲线，其余的与其类似。

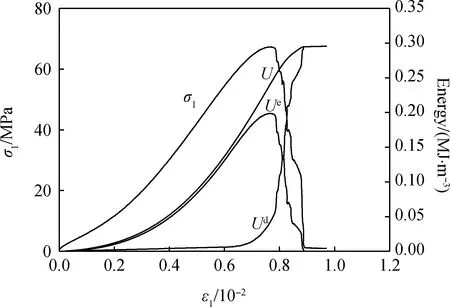
图3 砂岩单轴能量演化曲线Fig.3 Energy evolution mechanism curves of the sandstone under uniaxial compressive test

图3～图4为砂岩单轴和不同围压三轴压缩过程能量演化曲线，由图可知，吸收总能量经历快速非线性增加、线性增加和慢速非线性增加三个阶段，弹性应变能经历快速非线性增加、线性增加、慢速非线性增加和快速释放四个阶段，耗散能在屈服点之前基本为零，屈服点之后经历快速非线性增加直至试样破坏。

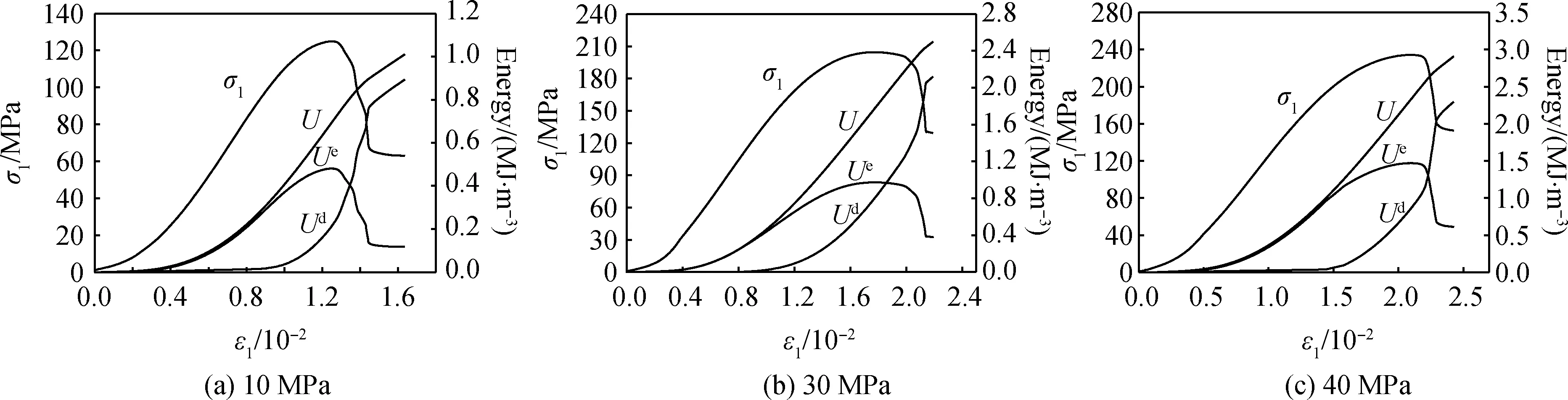
图4 砂岩三轴能量演化曲线Fig.4 Energy evolution mechanism curves of the sandstone under triaxial compressive test

(1)屈服点前，砂岩吸收总能量基本都以弹性应变能的形式存储，这一过程经历岩石的压密与弹性变形，很少产生内部损伤，故耗散能较小。弹性应变能的增速与吸收总能量的增速基本保持一致，并逐渐增大。

(2)屈服点与峰值之间，随着试验加载,砂岩试样不断吸收能量，仍以可释放弹性应变能的形式存储，该阶段弹性应变能增速减小，耗散能增速增大。该阶段内部损伤不断增加,强度逐渐丧失，内部损伤的形成和发展需要耗散能量，故耗散能增加速度较快。

(3)峰后阶段，存储在砂岩试样内部的弹性应变能瞬间释放，耗散能快速增加。释放的弹性应变能转化为岩样内部损伤形成和裂隙扩展所需的耗散能，使裂隙快速发展贯通，试样破坏。

由图3～图4可知，围压对砂岩能量演化的影响为：弹性应变能的线性增加段在单轴和低围压下显著，随着围压增大，弹性应变能的线性增加段逐渐消失；屈服阶段随着围压的增加，弹性应变能的增加速率越来越小，相应耗散能的增速越来越大，单轴时耗散能的增速最快，高围压下在屈服阶段后期，一定应变范围内砂岩弹性应变能基本保持定值，吸收的总能量基本全部转化为内部损伤和裂隙扩展所需的表面能。由此可知，单轴和低围压砂岩试样达到峰值时，内部损伤度较低，而高围压下砂岩试样达到峰值时，内部损伤度较高。同时可知内部损伤发展直至试样破坏时，单轴和低围压下经历轴向变形小，发展速度快，高围压下经历轴向变形大，发展速度相对慢。

图5为砂岩30 MPa初始围压下卸围压速率分别为1 MPa/s、0.1 MPa/s和0.01 MPa/s时的能量演化曲线，初始围压为10 MPa、20 MPa和40 MPa的能量演化规律与其相似，不再一一列出。由图5可知，卸围压过程能量演化分为三个阶段：加载阶段、卸围压稳定阶段和卸围压峰后段。每一阶段的能量演化特征为：

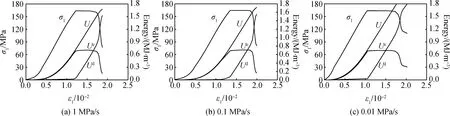
图5 砂岩卸围压能量演化曲线(30 MPa)Fig.5 Energy evolution mechanism curves of sandstone under different rates of the unloading confining pressure (30 MPa)

(1)加载阶段，该阶段与三轴压缩对应阶段相同，岩石吸收的能量以弹性应变能的形式存储，耗散能几乎为零。

(2)卸围压稳定阶段，由于是保持轴向压力不变，因此在该阶段弹性应变能的变化较小，基本保持水平状态，卸围压速率越小，保持稳定弹性应变能的能力越强。相同卸围压速率下，初始围压越大，弹性应变能维持稳定的时间越长。由于该阶段围压以不同速率减小，岩样侧向约束减弱，保持轴向压力不变的情况下轴向变形会持续增加，故外力继续做功，岩石继续吸收能量，由于该阶段弹性应变能基本保持不变，故岩样吸收的能量基本全部转化为耗散能，说明该阶段岩石吸收的能量全部用于岩样内部损伤与微裂隙发展所需的表面能，随着微裂隙增多、扩展，导致试样破坏。在卸围压的后期阶段，随着岩石内部损伤微裂隙的增多，岩石强度削弱，储存弹性应变能的能力减弱，原有弹性应变能随着围压减小也在缓慢释放，故卸围压后期，岩样内部大量裂隙的形成是岩样继续吸收能量和弹性应变能的部分释放导致的。从而可知，加载应力路径和卸围压应力路径下从能量角度分析岩样破坏机制具有显著差异。

(3)卸围压峰后段，该阶段弹性应变能全部释放转变为岩样破坏所需的表面能，与三轴加载相同初始围压状态相比，此时的围压由于卸载而减小，故其峰后阶段能量演化曲线变陡。

整体分析不同卸围压速率下吸收总能量、弹性应变能和耗散能的变化可知，岩样吸收总能量经历增速不断增加、增速恒定速率较大和增速恒定速率较小三个阶段，弹性应变能经历增速不断增加、基本保持定值和快速释放三个阶段，耗散能经历低速增加、快速增加和破坏陡速增加三个阶段。

3.2 能量比例特征

单轴、三轴加载和不同卸围压速率下砂岩破坏峰值时弹性应变能与吸收总能量的比值(Ue/U)如图6所示，Ue/U前面的数值表示卸围压速率，0表示三轴压缩试验。

由图6可知，砂岩单轴3个试样在峰值点Ue/U的均值为0.847 2，为所研究加载和卸围压应力路径下能量比的最大值。分析总体变化趋势可知，卸围压应力路径下峰值处Ue/U小于三轴加载应力路径下的比值。且卸围压速率越小，对应的Ue/U越小。随着围压的增加，或随着初始围压的增大，Ue/U总体在减小并趋于定值。三轴应力路径下Ue/U约趋于0.6，卸围压应力路径下Ue/U在0.4～0.6之间。随着初始围压的增大，卸围压速率对Ue/U的影响越加显著。

图6 砂岩加卸载条件下峰值能量比与围压关系Fig.6 Relationship between energy ratio at peak and confining pressure of sandstone under loading and unloading tests

图7为砂岩卸围压速率与Ue/U的关系，其前面的数值表示初始围压。由图7可知，随着卸围压速率的增大，Ue/U增大，卸围压速率在0.01～0.1 MPa/s之间，Ue/U增速较快，在0.1～1 MPa/s之间增速变缓。由总体变化趋势可知，相同卸围压速率下，初始围压越大，Ue/U越小。在0.01 MPa/s卸围压速率下，Ue/U受初始围压影响大，而1 MPa/s卸围压速率下，Ue/U受初始围压影响小。

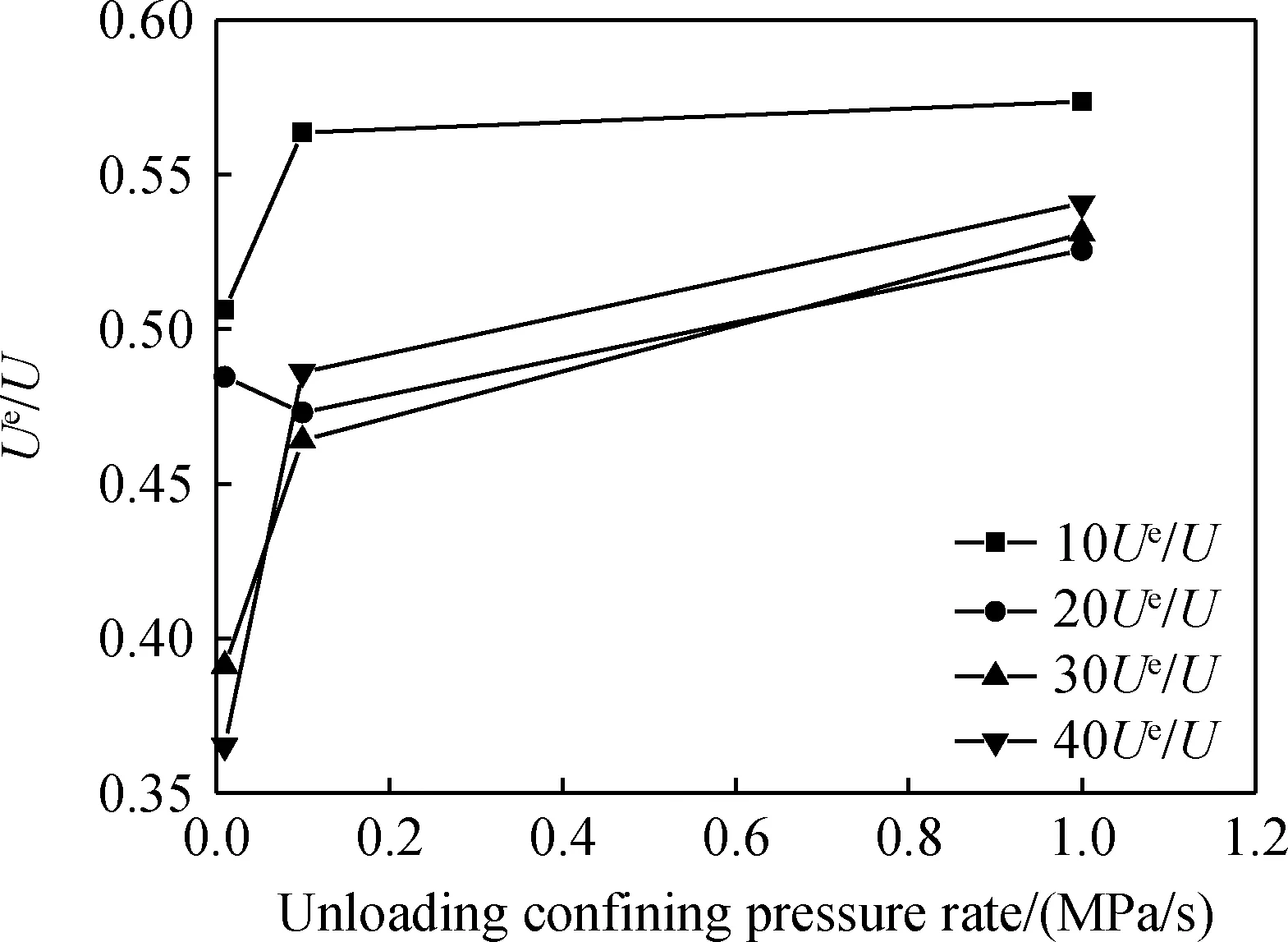
图7 砂岩卸围压速率与Ue/U的关系Fig.7 Relationship between unloading confining pressure rates and Ue/U of sandstone

3.3 弹性储能极限特征

砂岩加卸载条件下弹性储能极限与围压关系如图8所示。图8中1 MPa/s、0.1 MPa/s、0.01 MPa/s分别代表卸围压速率，0 MPa/s代表三轴加载。可见，砂岩弹性储能极限随着围压增大按线性规律增大。相同围压下，卸围压应力路径破坏对应的弹性储能极限小于三轴加载应力路径破坏时的弹性储能极限。表明同一围压下，三轴加载应力路径存储的弹性应变能大于卸围压应力路径下卸载到相应围压时的弹性应变能，同时表明加载应力路径相对卸围压应力路径能提高砂岩的弹性储能极限。

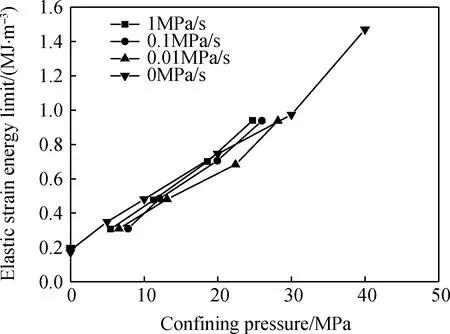
图8 砂岩加卸载条件下弹性储能极限与围压关系Fig.8 Relationship between the elastic energy limit and confining pressure under loading and unloading tests

3.4 讨论

以上分析可知，单轴、三轴和不同卸围压速率的卸围压应力路径对能量演化中弹性应变能和耗散能的变化有显著影响。

砂岩单轴时弹性应变能经历较短的慢速增加阶段即达到峰值，然后突然释放；三轴时弹性应变能在屈服阶段的慢速增加阶段随着围压的增大而增长，高围压下屈服阶段后期弹性应变能增速已很小；卸围压应力路径的卸载阶段，弹性应变能基本保持不变。砂岩单轴时耗散能出现较早，在屈服阶段后期快速增加；三轴加载应力路径下，早期耗散能较小，进入屈服阶段后，耗散能开始快速非线性增加，增速变得越来越大；卸围压应力路径下，从卸载开始，耗散能一直近似线性增加，直至试样破坏。