福建成品油管道停输后压力预测算法模型

邵晓 郑坚钦 戴元豪 张扬

1中国石化福建石油分公司

2中国石油大学（北京）

成品油管道的停输操作是管道在投产和运行过程中不可避免的[1]。停输时段的管道管理和安全监控也是必不可少的。在福建成品油管道停输期间，现场人员对于管内压力变化无法提前预测，当管内压力下降时，经常误以为是管道发生泄漏或出现打孔盗油事故，需现场人员巡检排查[2]，不仅增加了现场人员的工作量，也不利于控制运行成本。因此，有必要对管道建立停输时段压力变化模型，提前预测管内压力变化，监测管道停输状态。当检测值与预测值差别不大时，可以认为管内压力属于正常变化；而当两者差别较大时，很大可能发生泄漏等异常事故，应立即排查，保证管道安全。

目前，国内针对成品油管道停输的研究较少[3]，还没有建立停输时段管内压力变化的预测模型。随着我国成品油管道的快速投产和运行，对多条管道开始分析其停输的压力变化[4]。郭袆等[5]针对港枣成品油管道在计划停输期间频繁出现管内压力迅速下降的问题，根据管道相关数据，分别研究了温度对管内油品体积和管道压力的影响程度，结果表明油品温度的下降是导致管道停输压力出现下降的主要原因。陈春[6]研究了江阴—无锡成品油管道停输后压力变化情况，基于传热学和热力学理论，结合现场实际数据，建立油品压力温度变化模型，通过仿真模拟，提出修正系数，改进管道停输压力变化模型。

目前研究主要存在两个问题：①依托管内压力、温度变化的经验公式，建立机理模型或数值模拟来探究压力变化情况，由于现场环境的不确定性，模型与实际情况存在差别；②将环境温度设为定值，一定程度上影响模型的准确性。

福建成品油管道的泵出站口都设有温度计和压力表，已储存大量的停输管道数据。如何挖掘这些数据之间的规律，通过关联分析建立停输压力变化模型是现场管理人员目前思考的方向。随着人工智能和大数据时代的来临，基于数据驱动的机器学习算法在预测模型上发挥越来越重要的作用[7]。韩小明等[8]基于人工神经网络机器学习理论，建立油气管道完整性预测模型，提高了管道安全管理水平。胡群芳等[9]基于模型参数的概率分布，利用贝叶斯理论对燃气管道建立腐蚀深度预测模型，定量评估腐蚀安全问题。张新生等[10]基于现场实测数据和马尔科夫链模特卡洛算法，建立油气管道剩余寿命预测模型，应用于管道的可靠性评价中。

因此，本文将基于福建成品油管道已有的大量停输温度压力数据和目前流行的机器学习算法，针对管道出站检测点建立停输压力变化预测模型，监测管内压力变化情况。

1 管道停输机理分析

目前研究表明，由于成品油管道通常采用常温密闭输送方式，而管内油品具有膨胀性和压缩性的物理特性，基于传热学理论，管输油品和管道环境温度的差异是引起管道压力变化的主要因素。在管道停输初始阶段，由于管内油品温度明显大于环境温度，油品与管壁、管壁和土壤之间的热交换较强，管内油品下降速度快。随着停输时间的增加，油品与环境温差减小，管内温度下降速度随之减小。管道停输后油品温度随时间的变化已形成经验公式(1)[11]。当管道开始停输时，出站检测点可获取初始油温，以小时为单位，可以根据公式(1)求出停输一段时间后的管内油温变化。

式中：K为总传热系数，W/(m·℃)；D、D1、D2为管道平均直径、管道内径和管道外径，m；cy、cg为油和钢材的比热容，J/(kg·℃)；ρy、ρg为油和钢材的密度，kg/m3；T0为环境温度，℃；Tτ为停输τ小时后的油温，℃；TQ为开始停输时的油温，℃；τ为停输时间，h。

油温和管道环境的差异，使得管内油品体积发生一定程度的变化，从而导致管内压力的变化。随着油温的变化，管内压力的变化形成的经验公式为

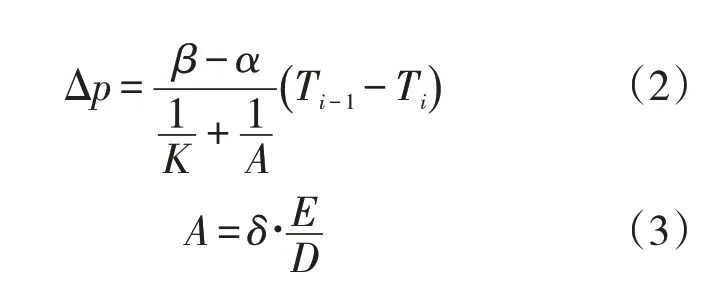
式中：α为管道的体积膨胀系数，管道为钢管时，α≈3.3×10-5℃-1；δ为管道壁厚，mm；E为管材的杨氏弹性模量，管道为钢管时，E≈2×1011Pa；β为油品的体积膨胀系数，℃-1；K为油品的弹性系数，Pa；Ti为第i时步的油温，℃；Ti-1为第i-1时步的油温，℃；Δp为第i时步与第i-1时步的压差，Pa。

由经验公式（1）和（2），可以得出管道压力变化的影响因素分为两类：一类是管道与土壤的固有属性，这些因素基本保持不变，在建立预测模型时可以当成参数，不考虑在内；另一类是可变因素，分别为停输时间τ、初始油温TQ、环境温度T0。在前人的研究中，环境温度一般取平均环境温度。但由于不同地区昼夜温差不同，为提高计算精度，本文通过气象网站获取停输期间内每个小时的具体温度值。通过以上分析，确定影响Δp的变量为τ、TQ和T0，因此，下面将建立基于τ、TQ和T0的压力预测回归模型。

2 建立管道停输压力预测模型

2.1 数据预处理

现场可通过管道运行系统导出停输时段各出站点的压力、油温和停输时间，缺少的是环境温度。借助爬虫技术在天气网站上获取各地区的历史温度，整理数据并建立停输管内压力变化预测数据库。

数据归一化是数据处理中非常重要的一步，其可以加快训练模型的收敛，提高预测精度。由于p以及变量τ、TQ和T0的取值范围不同，为了消除各变量之间的幅度影响，需要进行数据归一化。停输数据通过最小—最大归一化方法处理，每个维度的数据均被归一化为0～1范围内，如方程(4)所示：

其中，x*为归一化的值，xi为各变量原始值，xmax和xmin分别为各变量的最大值和最小值。

2.2 机器学习算法

（1）线性回归（Linear Regression，LR）：线性回归算法形式简单，就是能够用一个直线较为精确地描述数据之间的关系。通过输入变量的线性组合来预测目标值，是机器学习中非常重要的基本算法。特点是易于建模，方法简单，但无法拟合非线性关系。

（2）支持向量机（Support Vector Machine，SVM）：它是一种用于分类和回归的监督学习算法[12]。当用于分类时，基本思想是根据现有数据样本找到一个最大间隔的“超平面”，使得所有样本到“超平面”的距离最大。而对于回归预测问题，样本点最终只有一类，通过设定阈值计算损失，目的是使得所有数据的类内方差最小。

（3）决策树回归（Decision Tree，DT）：就是将特征空间划分成若干单元，每一个划分单元有一个特定的输出。划分的过程也就是建立树的过程，每划分一次，随即确定划分单元对应的输出，也就多了一个结点。当根据停止条件划分终止的时候，最终每个单元的输出也就确定了，也就是叶结点[13]。

（4）随机森林（Random Forest，RF）：它是指利用多棵决策树对样本进行训练并预测的一种算法，是一种集成学习算法[14]。通过对样本集自主采样和随机选择子集用于节点分割方式构建多个决策树，每次分裂时选择最好的特征进行分裂。最终通过所有决策树的均值确定预测结果。

（5）梯度提升（Gradient Boosting，GB）：它也是一种以决策树为基学习器构建的集成学习算法[15]。利用最速下降方法，即利用损失函数的负梯度在当前模型的值，不断迭代、不断构造回归树进行决策，而且每一个回归的样本数据均来自上一个回归树所产生的残差，主要目的是降低偏差。

2.3 模型评价指标

为了评估不同机器学习算法的预测效果，本文采用判定系数(R2)、平均绝对误差(MAE)和均方根误差(RMSE)作为预测模型的性能指标。即

其中，n为数据样本的数量；pi为预测模型压力输出值；ri为原始压力值。

3 现场验证

3.1 泉港南线出站点

图1 泉港南线出站管内压力随停输时间的变化情况Fig.1 Change of the pipeline pressure of Quangang South Station Outgoing Line with shutdown time

以福建成品油管道在2019年3月30日到4月11日停输期间泉港南线出站压力变化为例，压力变化如图1所示，部分数据如表1所示。为了提高预测模型的准确性，打乱样本数据并划分数据集。训练集、验证集、测试集的占比分别为70%、10%、20%。5个算法在测试集上的预测结果如图2所示，图3展示的是不同预测模型所对应的RMSE、MAE、R2。由图2和图3可知，LR和SVM预测结果与真实值差别较大，特别是LR，其R2只有0.329，RMSE和MAE的值也较大。因此，这两种回归预测模型不适合用于该管道的压力变化预测。对于DT、RF、GB，预测曲线与真实曲线几乎重合，RMSE和MAE的值都小于0.05。另外三者的R2也都大于0.970，其中RF的值最大，为0.981。预测结果说明DT、RF、GB模型适用于福建成品油管道停输的管内压力变化分析。

表1 泉港南线出站点部分数据样本Tab.1 Data sample of the outgoing point in Quangang South Line Station

图2 不同预测模型在泉港南线出站测试集上的预测结果Fig.2 Prediction results of different prediction models in the outgoing test set of Quangang South Line Station

图3 不同预测模型在泉港南线出站点的预测效果对比Fig.3 Prediction effect comparison of different prediction models in the outging point of Quangang South Line Station

3.2 黄塘溪东出站点

同样，以黄塘溪东出站点在2019年5月5日到19日停输期间压力变化为例，压力变化如图4所示。5个算法在测试集上的预测结果如图5所示，图6展示的是不同预测模型所对应的RMSE、MAE、R2。由图5和图6可知，LR和SVM预测结果与真实值差别较大，不适合用于该管道的压力变化预测。对于DT、RF、GB，其预测曲线与真实曲线十分相近，RMSE和MAE的值也都小于0.05。但DT的R2为0.953，小于RF的0.988和GB的0.975，因此RF的预测效果最佳。结合上述分析可知，DT、RF、GB模型适用于福建成品油管道停输的管内压力变化预测，其中RF准确度最高。

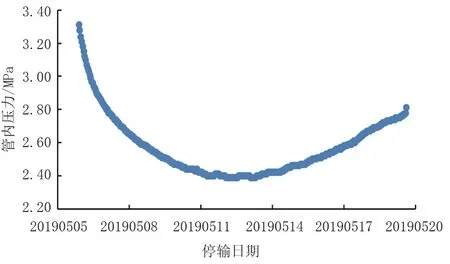
图4 黄塘溪东出站管内压力随停输时间的变化情况Fig.4 Change of the pipeline pressure of Huangtangxi East Station Outgoing Line with shutdown time

图5 不同预测模型在黄塘溪东出站测试集上的预测结果Fig.5 Prediction results of different prediction models in the outgoing test set of Huangtangxi East Station

图6 不同预测模型在黄塘溪东出站点的预测效果对比Fig.6 Prediction effect comparison of different prediction models in the outgoing poin of Huangtangxi East Station

4 结论

针对福建成品油管道停输再启动过程中管内压力变化无常的问题，建立了基于LR、SVM、DT、RF、GB的5种机器学习算法的压力预测模型，模型评价指标为RMSE、MAE、R2。以泉港南线和黄塘溪东出站为例，预测结果表明DT、RF、GB的R2可达到0.950以上，模型预测准确度高，可适用于福建成品油管道停输的管内压力变化分析。基于天气预报气温数据，该模型可预测未来时段管内压力的变化趋势，指导现场运行管理。该研究在其他成品油管道上同样具有运用的可能性。对于特定的成品油管道，通过获取现场的停输数据和当地的温度数据，即可代入建立的压力预测模型。但由于不同管道数据的差异性，最终得到的模型参数及效果会有所不同。