捷变正弦信号源波形建立时间的精确测量

2020-10-16梁志国张亦弛吴娅辉

计量学报 2020年9期

梁志国，何昭，刘渊，张亦弛，吴娅辉

(1.北京长城计量测试技术研究所计量与校准技术重点实验室，北京 100095；2.中国计量科学研究院，北京 100029)

1 引言

在动态测试与校准中，人们常会遇到波形变化和状态的切换，当信号波形或仪器设备从一个稳定状态切换到另外一个不同的稳定状态时，总会经过一段中间过渡状态，并花费一定的过渡时间。人们通常希望这种过渡时间越短越好，并且其破坏力或危险性越小越好。其中，最常使用并最具有明确物理意义的是阶跃过渡过程和阶跃信号波形的建立时间,它被定义为阶跃起始点时刻至波形完全进入最终状态的规定公差带的起始时刻之间的时间差值。而公差带则有5%、1%等不同的约定量值。并依此发展了放大器阶跃响应建立时间等相应的概念、方法及测量手段。对于阶跃信号以外的其它信号波形，无疑也有建立时间的问题，但由于波形本身的复杂性，其建立时间往往很难清晰、直观、简单地获取。因而，常用阶跃建立时间方式来分析和代替复杂波形的建立时间。这在仪器设备的设计、研制及生产厂家，多数情况下可以做到。但在用户和计量测试部门，则往往很难独立获取并精确评价它们。给其使用中的计量校准和技术状态确认带来额外的风险与隐患。尤其是正弦信号波形，在实际工作中获得了最广泛的应用，因而其波形状态切换所需的建立时间最具有代表性和典型性，对实际工作的影响巨大[1～9]。

通常，正弦波形的状态切换具体体现在以下几种应用状态：1) 信号源开机加载；2) 信号源参数的切换(幅度、频率、相位、偏移等参数的独立切换或组合切换)；3) 以正弦为载波的数字化脉冲调制波形(脉冲调幅、脉冲调频、脉冲调相)；4) 电子对抗中的跳频技术；5) 正弦信号源的过载恢复特性。由此可见，正弦波形的建立时间，是正弦信号源最重要的动态特性之一，多年以来，除了跳频问题以外，之所以未被特别关注，主要是其测量和表述未能获得彻底解决。

本文后续内容，将主要讨论正弦信号源波形建立时间的精确测量评价问题，同时，提出一种基于4参数正弦拟合的数字化测量方法，以简洁、直观地展示正弦波形状态切换时的过渡过程，并对其中的问题进行讨论。

2 原理方法

正弦波形建立时间测量的基本思想，首先，是使用数字示波器丰富的触发功能[10]，将其状态切换的过渡过程完整地采集记录下来，然后，进行波形分析。并且认定，在过渡过程完成后的波形，应该完全符合正弦规律，可以用四参数拟合方法对该部分进行正弦波形拟合，获得拟合参数。在此基础上，将波形按拟合规律向全体采样序列进行延展，获得采样序列与拟合回归波形之间的偏差序列，该偏差序列波形即完整反映了状态切换过程中正弦波形建立时的误差过渡过程。

定义：信号源由稳定的第一状态向稳定的第二状态切换时，切换起始时刻t1至切换过渡波形与第二稳定状态之间的偏差波形幅度永久进入约定平稳公差带的起始时刻t2之间的时间差为信号源切换过程的建立时间。即第二平稳状态的波形建立时间。

本文中，均以拟合回归标准偏差的3倍值定义状态切换的起始时刻和状态切换的完成时刻。具体过程如下：

设正弦波激励信号第一个稳定状态的信号波形为xa(t)，第二个稳定状态的信号波形为xb(t):

xa(t)=Ea(sin(2π(fat+φa)+da

(1)

xb(t)=Eb(sin(2π(fbt+φb)+db

(2)

式中：xa(t)、xb(t)为正弦信号的瞬时值；Ea、Eb为正弦信号幅度； fa、 fb为正弦信号频率；φa、φb为正弦信号的初相位；da、db为信号的直流分量值。当fa=0时，第一稳定状态为直流状态。

正弦波形的信号状态切换是由稳定状态xa(t)切换到稳定状态xb(t)上。

1) 如图1所示，将待测正弦信号源连接到数字示波器的测量通道，选取合适的内部或外部单次触发条件，以便有效抓取正弦波形的状态切换，并令其处于等待触发状态。在可能的情况下，可采用信号触发方式，否则，需要使用状态切换控制信号，以外触发方式触发采集测量。选取通道采集速率v，以使得所测正弦波形的每个周期内能有足够的采样点数(通常有20个以上的采样点数)；选取数据存储深度n，以使得所获得的采样序列能存储有两倍以上的正弦波状态切换过渡过程的时长。

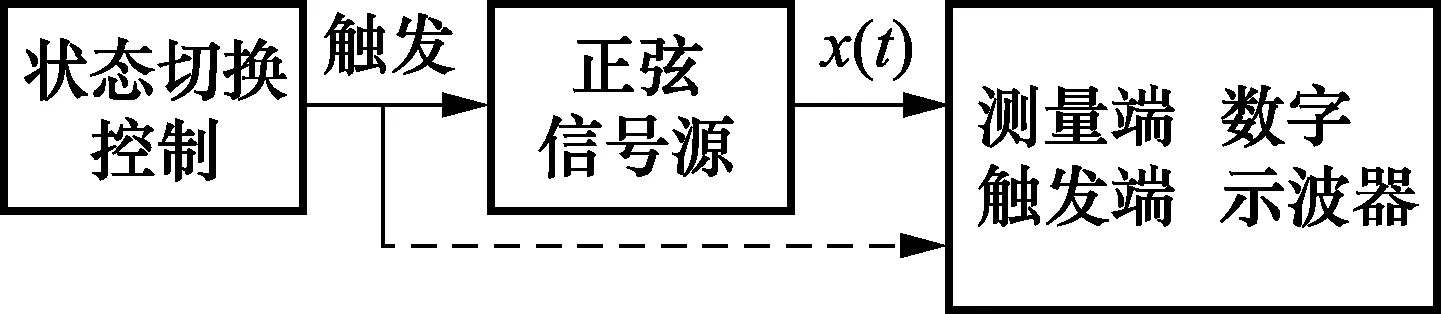
图1 正弦波建立时间测量框图Fig.1 Settling time measurement of sinusoidal generators

2) 启动正弦信号源由第一稳定状态向第二稳定状态的状态切换，触发采集，获得含有完整正弦信号切换过渡过程的采集序列xi(i=0，…，n-1)。

3) 从采集序列远离过渡过程的第二稳定状态xb(t)采集数据中截取长度为n2的子序列xqk(k=0,…,n2-1)，按最小二乘法求出xqk(k=0,…,n2-1)的拟合信号[11～15]：

xq(t)=Aq·sin(2π·fqt+φq)+dq

(3)

式中：xq(t)为拟合信号的瞬时值；Aq为拟合正弦信号的幅度； fq为拟合正弦信号的频率；φq为拟合正弦信号的初相位；dq为拟合信号的直流分量值。

由于采集数据是离散值xi，对应时间也是离散的ti，ti=i/v，(i=0，…，n-1)。这样，式(3)变成了：

xq(tqk)=Aq·sin(2π·fqtqk+φq)+dq

简记为：

xq(k)=Aq·sin(ωq·k+φq)+dq

ωq=2π·fq/v

(4)

则，实际有效值误差ρq为：

(5)

式中：tqk为序列xqk(k=0，…，n2-1)第k个测量点的时刻(s)。

当ρq最小时，获得式(2)的拟合正弦波信号式(4)。

4) 将第二稳定状态的拟合波形拓展到全体采样序列，则：

xq(i)=Aq·sin(ωq·i+φq)+dq,i=0，…，n-1

获得拟合回归偏差序列为：

Δxq(i)=xi-xq(i),i=0，…，n-1

(6)

以3ρq为公差带，寻找绝对值|Δxq(i)|≤3ρq的起始时刻点，其右侧相邻时刻点t2即为第二稳定状态结束过渡过程时刻点。

5) 从采集序列未切换到过渡过程的第一稳定状态xa(t)采集数据中截取长度为n1的子序列xpk,(k=0,…,n1-1)，按最小二乘法求出其拟合信号：

xp(t)=Ap·sin(2π·fpt+φp)+dp

(7)

式中：xp(t)为拟合信号的瞬时值；Ap为拟合正弦信号的幅度； fp为拟合正弦信号的频率；φp为拟合正弦信号的初相位；dp为拟合信号的直流分量值。

xp(tpk)=Ap·sin(2π·fptpk+φp)+dp

简记为：

xp(k)=Ap·sin(ωp·k+φp)+dp

(8)

ωp=2π·fp/v

则，实际有效值误差ρp为：

(9)

式中：tpk为序列xpk(k=0，…，n1-1)第k个测量点的时刻(s)。

当ρp最小时，获得式(1)的拟合正弦波信号式(8)。

6) 将第一稳定状态的拟合波形拓展到全体采样序列，则：

xp(i)=Ap·sin(ωp·i+φp)+dp

获得拟合回归偏差序列为：

Δxp(i)=xi-xp(i),i=0，…，n-1

(10)

以3ρp为公差带，寻找绝对值|Δxp(i)|≤3ρp的起始时刻点，其左侧相邻的时刻点t1即为第一稳定状态切换到过渡过程的时刻点。

特例，若fa=0，则第一稳定状态为直流，序列xpk(k=0,…,n1-1)的拟合曲线即为其算术平均值：

(11)

(12)

7) 则正弦信号的建立时间tset为：

tset=t2-t1

(13)

3 实验验证

对正弦信号建立时间tset精确测量方法的实验验证，使用Agilent公司的81160A型合成信号源提供正弦信号，采用幅度切换和开关启动两种方式进行切换，其第一稳定状态近似直流，第二稳定状态为正弦波形。

用RIGOL公司的DS1104型数字示波器进行数据采集，其A/D位数为8 bits，带宽100 MHz，最高通道采样速率为1 GSa/s，有4个独立测量通道。

3.1 幅度切换实验

用合成信号源81160A输出幅度25 mV频率 5 kHz 的正弦波激励(幅度小与一个A/D量化台阶，相当于直流叠加噪声)，切换到幅度5 V的同频正弦波。用数字示波器DS1104的通道1对其进行同步采集。其通道1的量程为2 V/div；通道采样速率 5 MSa/s，通道采集数据个数n=15 000。上升沿触发，触发电平设为2.68 V。启动幅度切换，获得采集波形，图2中的曲线1为其正弦波形建立时过渡过程附近的部分采集波形，曲线2为拟合回归偏差波形Δxq(t)。

图2 正弦波形建立时间过渡过程Fig.2 Settling time of sinusoidal waves

从曲线1的状态切换后稳定段中，取n2=7 500，按上述过程获得拟合正弦幅度Aq=5.020 420 V，频率fq=5 000.062 Hz，初始相位φq=-174.400°，直流分量dq=-11.838 mV，有效值误差为ρq=9.193 mV。由曲线2可得t2=934.2 μs。

按式(13)得tset=t2-t1=878.6 μs。

其它条件不变，仅仅变换一下信号频率，获得的正弦波形建立时间如下表1所示。

表1 不同信号频率的正弦波形建立时间Tab.1 Settling time of sinusoidal waves via frequency

3.2 开关启动实验

用合成信号源81160A在输出幅度5 V频率 50 kHz 的正弦波激励状态设置时，通过开关按键开机输出正弦波形。用数字示波器DS1104的通道1对其进行同步采集。其通道1的量程为2 V/div；通道采样速率31.25 MSa/s，通道采集数据个数n=15 000。上升沿触发，触发电平设为1 V。按动合成信号源开关，获得采集波形，图3中的曲线1为其正弦波形建立时过渡过程附近的部分采集波形，曲线2为拟合回归偏差波形Δxq(t)。

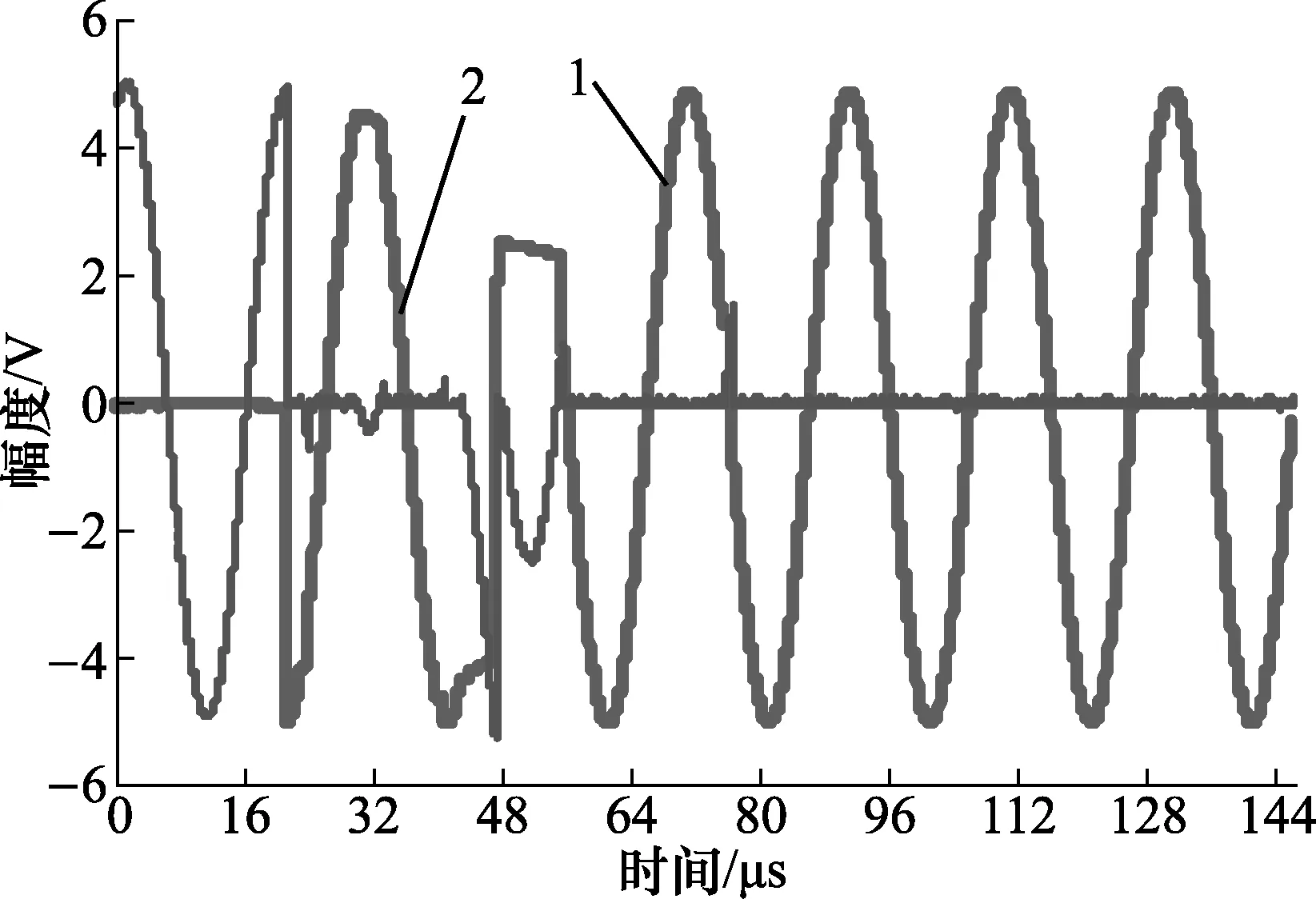
图3 正弦波形建立时间过渡过程Fig.3 Settling time of sinusoidal waves

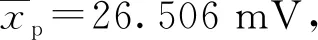
从曲线1的状态切换后稳定段中，取n2=7 500，按上述过程获得拟合正弦幅度Aq=4.981 839 V，频率fq=5 000.18 Hz，初始相位φq=-158.064°，直流分量dq=-14.336 mV，有效值误差为ρq=9.321 mV。由曲线2可得t2=76.48 μs。

按式(13)得tset=t2-t1=55.20 μs。

其它条件不变，仅仅变换一下信号频率和采集速率，获得开关启动时正弦波形建立时间如表2所示。

3.3 实验分析

从上述实验结果可见，状态切换时正弦波的建立时间具有很大的差异，在所涉及的信号源上，同频幅度切换所需要的建立时间远远大于硬开关启动所需要的建立时间，两者相差近20倍！从而也看出建立时间测量评价的重要性和必要性。

另外，可以看到，幅度切换所导致的过渡过程变化比较平稳，基本上是幅度单调增加，而偏差在单调降低。但是开关启动造成的切换则不然，正弦建立的过渡过程中，幅度并非单调增加，偏差也不是单调降低，往往会有较大的干扰波动间歇出现，应该属于按键开关接触不良等导致的电火花飞弧等众多因素造成的影响，也是实际工作中必须要考虑的物理现象。

表2 开关启动时正弦波形建立时间Tab.2 Settling time of sinusoidal waves at turn on

最后，可以看出，同种状态条件下的建立时间测量结果具有一定的稳定性，和信号频率等变化关系不大，但采样间隔对其影响不容忽视，当采样间隔较大时，很容易造成较大的测量误差。在实际测量中应予以重视。

4 不确定度分析

由式(13)可见，正弦信号的建立时间的测量主要受以下几个因素的影响：

1) 时刻点t1的起始判据ρp及其稳定性与复现性，以及正弦波建立时的过渡过程曲线1在时刻点t1处的曲线斜率g1；

2) 时刻点t2的起始判据ρq及其稳定性与复现性，以及正弦波建立时，拟合回归偏差波形曲线2在时刻点t2处的曲线斜率g2；

3) 采集序列的随机噪声与量化误差；

4) 采样时间间隔；

5) 建立时间的测量重复性。

4.1 直流部分曲线段

当时刻点t1之前的曲线为直流时，参数ρp的不确定度为[16～18]：

(14)

ρp给t1带来的不确定度为：

(15)

实际上，采集序列的随机噪声与量化误差的有效值就是ρp，因而，它们造成的t1点幅度不确定度为：

un(x)=ρp

(16)

噪声与量化给t1带来的不确定度为：

(17)

采样间隔为1/v，它给t1带来的误差被认为在区间[-0.5/v,0.5/v]内服从均匀分布，因而，采样间隔给t1带来的不确定度为：

(18)

4.2 正弦部分曲线段

将正弦参数拟合与直线参数拟合同等看待，当时刻点t1之前的曲线为正弦波形时，参数ρp及噪声与量化给t1带来的不确定度依然可以按照式(14)～(18)等同估计。

同理，时刻点t2之前的曲线为正弦波形，参数ρq的不确定度为：

(19)

ρq给t2带来的不确定度为：

(20)

采集序列的随机噪声与量化误差的有效值是ρq，因而，它们造成的t2点幅度不确定度为：

un(x)=ρq

(21)

噪声与量化给t2带来的不确定度为：

(22)

采样间隔给t2带来的不确定度uv(t2)与给t1带来的不确定度uv(t1)相等，可按式(18)估计。

4.3 合成标准不确定度

由于上述各个不确定度分量均是通过模型化方法获得，可以按照它们之间互不相关来进行处理，由此得到正弦波形建立时间的测量不确定度为：

(23)

式中：ua为建立时间tset的测量重复性带来的不确定度，以实验标准偏差方式估计。

由式(23)可见，正弦波建立时间的不确定度主要受采样速率、拟合残差有效值、时刻点处的曲线斜率等因素影响。增加采样速率可以降低不确定度，调整时刻点的判据，使其附近的曲线斜率增加，也可以降低不确定度。当然，对测量曲线进行适当滤波，降低拟合残差有效值，也能降低测量不确定度。

5 问题讨论

本文所述方法在实际运用中，可望解决正弦波形建立时间的精确测量与校准问题，但仍然有一些问题需要特别予以关注。

首先是状态切换的过渡过程的有效抓取问题。这方面问题的解决，主要可以从数字示波器众多丰富的触发功能中寻找和构建触发条件。通常，涉及到幅度跳变、频率捷变、毛刺影响、尖峰、浪涌、过载恢复等状态切换过程的抓取，基本上都可以通过已有触发功能及其条件组合实现。只有以相位跳变实现为特征的脉冲调制过程的建立时间测量，触发抓取难度较大，可以通过深存储方式进行长序列测量存储，再从中寻找出相位跳变点；或者使用状态切换控制信号进行外触发方式获得相位跳变的过渡过程。

其次，是由一段正弦波形切换到另一段正弦波形的双正弦切换，其完整分析需要进行两次正弦拟合。一次是切换点之前的正弦波拟合，并以此寻找到状态切换点t1；另外一次是状态切换之后达到稳定状态的正弦波拟合，并以此寻找到过渡状态结束点t2。关于拟合数据段的截取，需要确保使用过渡过程以外的稳定正弦波形部分进行，否则，将可能导致拟合不收敛，或收敛到不希望的错误状态上。

另外，本文上述示例中，信号源均是从近似零状态跳变到正弦输出状态，其过渡过程本身体现的是完整的正弦波形建立过程，实际工作中面临的状态要复杂得多，当其从一个大幅值正弦波切换到一个小幅值正弦波时，其过渡过程体现的内涵还要包括电路放电效应过程外的过载恢复过程。

最后，需要说明的是，若进行不确定度评定时，两个时刻点的斜率计算均需要从其自身位置向斜率大的方向差分获得。