基于标准球距离约束的工业机器人参数标定

陆 艺，葛文琦，郭 斌

(1.中国计量大学 计量测试工程学院，浙江 杭州 310018；2.杭州沃镭智能科技股份有限公司，浙江 杭州 310018)

1 引 言

对工业机器人的重复定位精度要求很高，但由于机器人结构参数误差、自身重量、制造装配和温度的影响导致绝对定位精度偏低，这使得工业机器人在应用时产生误差影响操作结果。研究表明：连杆几何参数误差对机器人末端精度影响较大，90%左右的机器人可以通过对结构参数的标定来降低其末端位置的误差[1～3]。工业机器人标定技术是应用先进的测量仪器进行位姿测量，然后建立模型来得到准确的机器人运动学参数的过程，是提高机器人绝对定位精度的有效途径[4～6]。杨丽红等[7]利用激光跟踪仪根据扭转角的定义拟合出机器人的扭转角，并在末端误差模型的基础上运用最小二乘法辨识了运动学参数，两次标定之后最大误差较标定之前改善了98.327%，算术平均误差改善了96.613%；车亚肖等[8]基于机械臂和球杆仪所组成的闭链的几何约束条件和末端位置误差模型建立了参数误差辨识模型，使用非线性最小二乘迭代法[9～11]求得了集合参数误差，标定后轨迹1的精度提高了80.51%，轨迹2的精度提高了83.77%；Richter L等[12]将红外相机固定在三脚架上，在机器人的臂上设置标记点，由相机得到标记点的位移，并用最小二乘法完成了机器人的标定。使用先进的测量仪器标定机器人的方法需要昂贵的测量设备或者专业的人员进行操作。近年来，研究者开始对简易的测量方法进行探索研究，提出了一些不需要额外测量设备的约束标定方法。夏天等[13]利用虚拟封闭运动链的闭环方法完成了对工业机器人的标定，标定结果中平均偏差提高了81.38%。

本文提出了一种利用标准球和距离约束的标定方法来提高六轴串联工业机器人精度。基本步骤是设计了可改变方向的三角标定平台，平台上连接了3个标准球；将接触式测头安装在机器人末端的法兰盘上，用测头分别探测的标定平台上的3个标准球；将每个探测点的关节角度记录下来，对这些探测位置进行最小二乘拟合得到球心坐标，并将每2个标准球的球心距分别和三坐标测量机上测量得到的球心距的误差最小化，用Levenberg-Marquardt(简称LM)算法迭代辨识出运动学参数。该方法不需要外部昂贵的测量设备，成本较低且操作简单。

2 机器人运动学模型

工业机器人标定过程包括建立运动学模型、位姿测量、参数辨识和误差补偿。建立机器人运动学模型是运动学参数辨识的基础，由运动学模型得到辨识的误差模型， 从而求解误差方程的方程组完成参数辨识过程，得到所需的运动学误差参数。

2.1 运动学模型的建立

为了便于描述工业机器人连杆之间的运动，在机器人每个关节处建立坐标系得到运动学模型。工业机器人运动学模型中传统建模是D-H(Denavit-Hartenberg)模型[14,15]。以FANUC公司的LR Mate 200iD六轴串联机器人为例，首先进行D-H建模，根据D-H模型的定义在每个关节处建立坐标系，ai,αi,di,θi(i=1,2,…,6)为工业机器人各连杆参数。其中，ai代表连杆长度，为zi和zi+1沿xi轴平移的距离；αi代表连杆扭角，为zi和zi+1绕xi轴旋转的角度；di代表偏置，为xi-1和xi沿zi轴平移的距离；θi代表关节角，为xi-1和xi绕zi轴旋转的角度。工业机器人的坐标系关系如图1所示。

图1 机器人的坐标系关系图Fig.1 Robot coordinate diagram

通过在各个关节处建立坐标系得到各连杆间的齐次变换矩阵为：

(1)

式中：i=1,2,…,6。

当机器人存在关节轴线平行或接近平行时,D-H模型不具备完整性和连续性。为避免模型的奇异性，MDH(Modified D-H)模型引入了绕y轴旋转参数βi，则齐次变换矩阵变为

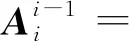
(2)

对于6自由度的串联机器人，机器人末端位姿的位姿矩阵的计算如下：

(3)

式中：n(nx,ny,nz),o(ox,oy,oz),a(ax,ay,az)表示机器人末端执行器相对于基坐标系{O0x0y0z0}的姿态向量;p(px,py,pz)表示机器人末端执行器的位置向量。

根据图1的运动学模型并结合其运动学参数列出了参数表,D-H名义值如表1所示。

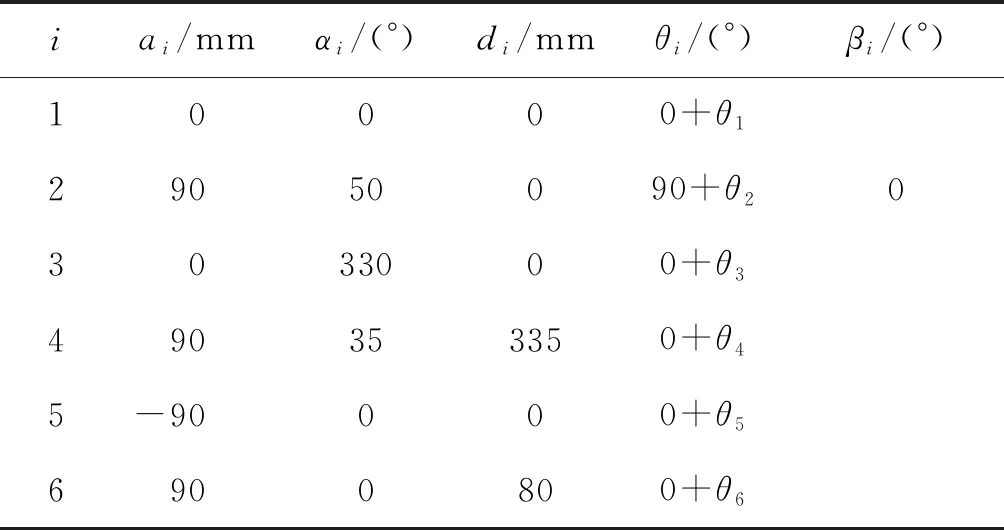
表1 机器人运动学参数名义值Tab.1 Nominal values of robot kinematic parameters

2.2 运动学误差模型

(4)

3 基于标准球距离约束的运动学参数标定

3.1 标定原理

本文选用FANUC公司的LR Mate 200iD六轴串联机器人进行基于标准球距离约束的运动学参数标定。高精度接触式测头选用海克斯康公司的型号为41.00-PP，重复精度为2 μm的接触式测头，该测头配有红宝石探针，标定系统如图2所示。

图2 机器人标定系统图Fig.2 Robot calibration system diagram

搭建了一个三角标定平台，由基座、万向节、平台面板和3个圆度为1.5 μm、直径为25.4 mm的陶瓷标准球组成，如图3所示。将3个陶瓷标准球连接在平台上，每2个球之间的理论距离为 300 mm，万向节可以改变平台面板的方向，从而改变3个标准球在空间的坐标，使机器人在探测球面上的点时尽可能包括更多的位姿。将接触式测头安装在机器人末端执行器上，通过控制机器人低速移动带动测头来探测标准球上的点，当探头碰到球体表面时，测头触发信号使机器人停止运动，读取并记录此时的关节角。

图3 标定平台系统实物图Fig.3 Platform system physical map

实验时，首先在一个标准球上用相差较大的位姿均匀探测的20个点，标定平台系统如图4所示。分别在球体顶部和底部各取一个点，3条圆线分别是北纬45°线、赤道线和南纬45°线，每条线上均匀取8个点，记录机器人在每个点时的关节角的值(θ1,θ2,θ3,θ4,θ5,θ6)。将这20个位置的关节角组成30组关节角集合，每个关节角的集合包含该20组关节角中的10组不同关节角并求得10组末端位置，由这10个末端位置拟合出该标准球的球心，总计得到30组球心坐标。同理在另2个标准球中分别求得30组球心坐标，进而求得球1和球2、球2和球3、球1和球3的球心距。通过改变标定平台的方向来获得不同的球面坐标，改变5次平台方向，每个球心距将获得15组不同球心距，共计450组球心距的值。用每2个球之间的球心距和用三坐标测量机测量出来的实际距离之间的距离误差组成标定方程，用LM算法迭代计算出运动学参数。

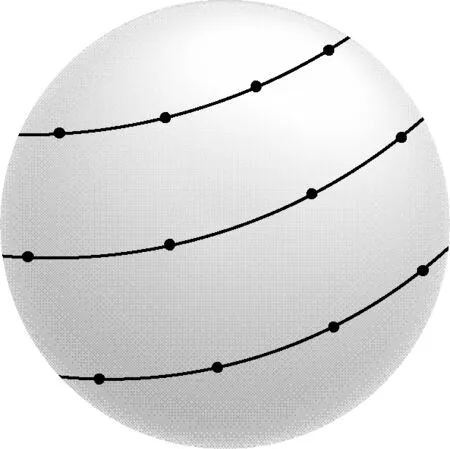
图4 球面取点图Fig.4 Spherical point map

本方法搭建的标定平台使用标准球之间的相对距离进行标定，可以在小范围内改变标准球在基坐标系下的位置，简单、快速地取得大量实验数据和用于验证的数据，更好地辨识出标定参数。

3.2 辨识参数的误差模型

对标定平台上的3个标准球分别编号为1，2，3，控制机器人运动使测头探针触碰标准球的表面，探测第j个球(j=1,2,3)上的20个点，每组取10个关节角组成30组关节角集合，记为jθk，其中k=1,2,3,…,30，则由这些关节角通过正运动学方程求得的末端位置jp′k(x,y,z)。

使用最小二乘法拟合出每个标准球的球心坐标jck(jcxk，jcyk，jczk)，标准球的半径为R，则球面方程可以写为：

(x-jcsk)2+(y-jcyk)2+(z-jczk)2=R2

(5)

将方程(5)展开并移项得：

(6)

(7)

将上式写成AX=Y的形式，用最小二乘法即可求出待求参数X，表达式为：

X=(ATA)-1ATY

(8)

求解式(8)即可得到我们所需的球心坐标jck(jcxk，jcyk，jczk)和R。

接下来使用两标准球球心之间的距离来进行标定。将2个球心的坐标看成球心距离的2个端点，以球1和球2间的距离为例，由两点间的距离公式可得标准球1和标准球2之间的球心距1-2dk为

(9)

f(1θk,2θk,η)=1-2dk(1θk,2θk,η)-1-2D

(10)

式中:η=(Δa1,…,Δa6;Δα1,…,Δα6;Δd1,…,Δd6;Δθ1,…,Δθ6;Δβ2)T为工业机器人的25个待辨识的误差参数。

4 辨识算法

待求解的式(10)是一个非线性方程组，其中隐含了工业机器人的运动学参数误差和平台球心距的对应函数关系。非线性高斯-牛顿最小二乘法是一种经典解非线性方程组的方法，由于实际计算中高斯-牛顿法经常会出现不收敛或者局部收敛的现象，因此选用LM法来进行迭代求解。

4.1 参数可行性分析

在工业机器人的辨识误差方程中会存在无法辨识出来的参数，称为冗余参数。冗余参数包括两类：一类是对末端位置误差无影响的参数，表现为在雅克比矩阵中某一列全为零；另一类是呈线性相关的参数，表现为雅克比矩阵中的列与列之间出现线性相关的现象。通过对辨识过程中的雅克比矩阵进行QR分解可以得到无法辨识的冗余参数：

(11)

式中：Q为r×r的正交矩阵；R为c×c的上三角矩阵；0(r-c)×c为(r-c)×c的零矩阵；r为测量点的个数；c为误差参数的个数。

式(11)中的矩阵R上对角线的值为0的元素所对应的参数是无法识别出来的冗余参数，将雅克比矩阵J中相对应的列元素剔除，即可得到可辨识的方程组，从而更好地辨识出运动学参数，提高参数辨识的鲁棒性。其中，由于基坐标系和关节1重合，Δa1，Δα1，Δθ1，Δd1对末端位置没有贡献，应当从模型中剔除；连杆坐标系中关节2和关节3平行时，Δd2和Δd3对末端位置的影响是一致的，当引入旋转参数误差Δβ2时可剔除Δd2保留Δd3；当测头所在的工具坐标系和关节6同轴时，Δθ6同样对末端位置没有影响，应当剔除。计算后得有效的误差参数为η=(Δa2,Δα2,Δθ2,Δa3,Δα3,Δd3,Δθ3,Δa4,Δα4,Δd4,Δθ4,Δa5,Δα5,Δd5,Δθ5,Δa6,Δd6,Δβ2)T共18项。

4.2 LM非线性算法

LM非线性算法是对高斯-牛顿法的修正，能够解决高斯-牛顿法在计算过程中雅克比矩阵的奇异问题，并且提高计算精度。将第2节中的距离误差函数式(10)最小化为：

教师通过点击“管理”菜单中的“学生”选项打开添加学生页面，通过浏览选择或搜索已注册到Moodle平台中的学生用户，手工添加学生到课程中，同时赋予学生进入学习网站时可以使用模块功能的权限.

(12)

定义

式中：J为辨识方程的雅克比矩阵；m为迭代次数。

把误差矩阵F在待辨识参数ηm处泰勒展开，略去二次及二次以上的项，可近似写成方程形式如下：

(13)

式中：Δηm为第m次迭代时运动学参数误差的修正值；I为单位矩阵；λ为阻尼因子且λ>0，迭代的具体算法如下：

步骤2：计算第m次迭代的球心距误差矩阵Fm和雅克比矩阵Jm；

步骤4：根据ηm+1=ηm+Δηm更新运动学参数；

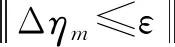
步骤6：若Fm+1≥Fm，更新阻尼因子，令λ为10λ，返回步骤2重新计算Δηm；

步骤7：输出最后所需结果ηm即为所需求的运动学参数误差值。

5 辨识结果分析

5.1 实验结果分析

在每个平台方向上使用接触式测头分别在3个标准球上探测点，记录下相应关节角值，经过最小二乘拟合后通过第3节介绍的迭代算法得到两两标准球之间的距离。旋转万向节改变平台的方向，重复上述步骤进行其他4个平台方向的实验方程求解。由于计算量较大，选用矩阵计算功能强大的MATLAB编写算法程序进行计算，辨识出的各运动学参数如表2所示。

表2 辨识的运动学参数结果Tab.2 Identification of kinematic parameter results

5.2 误差补偿

误差补偿是将辨识出的运动学参数误差补偿到运动学参数名义值中得到准确的运动学参数值，从而达到补偿的目的[17～19]。由于机器人的名义运动学参数在出厂时已确定无法修改，因此通过离线补偿的方法在笛卡尔空间来进行误差补偿。在机器人控制器中指定理论末端位置，将名义运动学参数值代入逆运动学方程中得到名义关节角θ，再将所得的关节角θ和辨识后的运动学参数值代入到正运动学方程中得到机器人实际的末端位置，以此实际末端位置作为指令位置，控制机器人运动到该位置后进行验证实验。分别在每个球面上取10个指定位置，并用上述方法求得10个实际末端位置，用最小二乘拟合得到球心坐标，进而求得每2个球之间的球心距。用补偿后的实际运动学参数求得的球心距分别与三坐标测量机测得的球心距进行比较，进行了5个平台方向的实验进行验证，每个平台方向有3组球心距，共计15组球心距，标定前和标定后的球心距误差如表3所示。

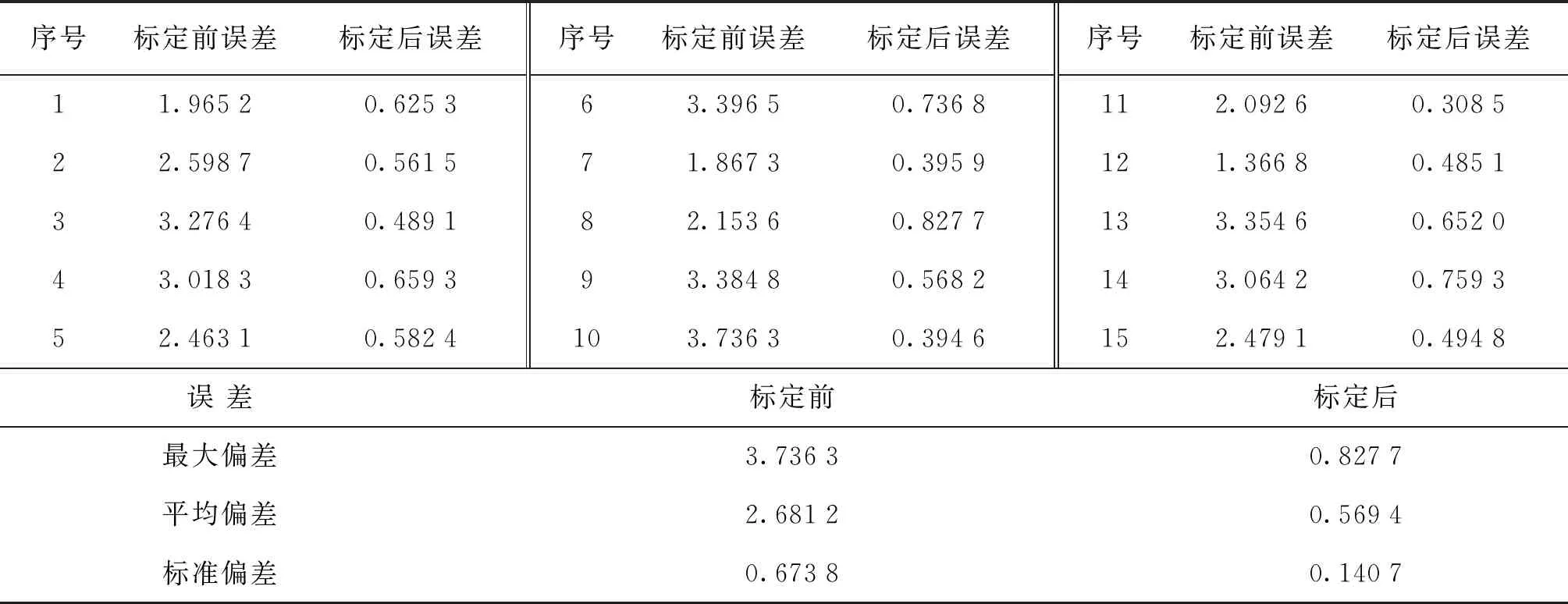
表3 球心距标定前后误差对比Tab.3 Comparison of errors before and after centroid distance calibration mm

由表3的数据分析可知，标定前和标定后的距离误差相比，最大偏差由3.736 3 mm减小到 0.827 7 mm，减少了77.85%；平均偏差由2.681 2 mm减小到0.569 4 mm；减少了78.77%；标准偏差由 0.673 8 mm 减小到0.140 7 mm，减少了79.12%，从而证明了此标定方法提高了工业机器人的定位精度。

6 结 论

针对工业机器人绝对定位精度较低的问题，建立了MDH模型，消除了传统D-H模型的在平行关节处的奇异性问题。提出一种基于标准球和距离约束的标定方法，通过在机器人末端执行器安装接触式测头，将标定平台的固定球心距离作约束条件，使机器人末端探针探测得到的球心距和其实际距离的误差最小化，最后利用LM算法辨识出准确的运动学参数。实验结果表明：标定前的平均偏差和标准偏差与标定后的相比有明显的减小，有效地提高了工业机器人的绝对定位精度。