二维材料自旋极化及光学性质调控理论研究

任俊峰 杨 哲 郭甲田

( 山东师范大学物理与电子科学学院，250358，济南 )

1 引 言

2004年，Novoselov等人[1]采用微机械剥离法首次制备出石墨烯，这打开了二维材料的研究之门.二维材料是指厚度只有一个或几个原子层厚度的材料，电子只能在两个维度自由运动.二维材料特别是石墨烯材料具有出色的力学和机械性能，如高面内刚度和强度以及极低的抗弯强度等[2]，这使得它可以应用在可拉伸、可折叠设备以及可穿戴触觉传感器中[3, 4].首款石墨烯触摸屏智能手机于2014年由2D Carbon发布，该手机广泛使用石墨烯来获得冷却和能源方面的增益[5, 6].如今，二维材料的世界越来越丰富，按照组成成分不同，二维材料分为：单质类(如石墨烯、黑磷等)、非金属化合物(如六方氮化硼、石墨型氮化碳等)、金属化合物(如层状金属三氧化物、金属卤化物、金属磷三硫族化物、过渡金属氧化物等)、盐类(如无机钙钛矿型化合物、黏土矿物等)、有机物(如层状金属有机骨架化合物、层状共价有机骨架化合物等)[7].

图1 由石墨烯得到的三种碳结构

作为碳家族的典型成员之一，石墨烯的出现打破了二维材料无法在常温常压下稳定存在的理论预言.石墨烯具有二维六角蜂窝状的层状结构，由sp2杂化的碳原子紧密连接构成.它可以包裹成零维布基球，卷成一维碳纳米管，或者堆叠成三维石墨[8]，如图1所示.石墨烯的合成方式主要有自上而下(微机械剥离法等)和自下而上(化学气相沉积法等)的两种方式.微机械剥离法是利用胶带破坏晶体片层间的范德瓦尔斯力，步骤是将块状材料黏附在胶带上，再用另一条胶带去黏附、剥离.而化学气相沉积法是将一种或几种气相前驱体循环通入反应炉中，高温下在基底表面发生反应或分解，从而得到所需二维材料.目前使用较多的是化学气相沉积法[1,9].石墨烯具有许多典型的特征，如具有优异的电学，热学，光学等性质，同时石墨烯还具有零带隙、高电子迁移率、高电导率(106s/m)、高导热性、量子霍尔效应以及较高的光吸收特性等[10]，这使得石墨烯在诸多器件中有广阔的应用前景[11-15].例如，由于单层石墨烯的透光率高达97.7%，石墨烯如此优异的光学性质使其可以应用在液晶显示屏中[5,15].常温下，石墨烯的载流子迁移率高达2.0×105cm2/(V·s)，约是硅的140倍[13]，利用石墨烯的这一性质，IBM于2008年率先制成石墨烯晶体管并利用其制备了世界上首个石墨烯光电探测器[10, 16].在储能方面，石墨烯等二维材料有较高的比表面积，因此能够容纳更多的Li+，可以作为锂电池的正极材料[17].在超级电容器方面，石墨烯也具有很大的应用优势，理想的超级电容器要有高能量密度而不伴随功率密度的降低.电极材料的表面积和导电性是超级电容器性能的主要影响因素，石墨烯具有高比表面积和高导电性，可以作为一个较好的备选材料[18].另外，石墨烯具备优异的光电学性能，可以作为光伏器件的功能组件来促进环境保护和可再生能源的利用，如用作有机太阳能电池和染料敏化太阳能电池的透明电极等[19,20].利用石墨烯等二维材料可以制备具有高通透性、选择性、抗菌性和吸附性等特性的薄膜，在环境领域的应用中具备优势，如石墨烯在环境治理中的水或空气处理方面就具有很大的应用潜力[21].

二维材料还在自旋电子学领域获得了广泛研究.电子的自旋特性所引起的量子效应是凝聚态物理和材料物理中许多奇妙现象的根源.自旋电子学的研究主要利用电子自旋作为信息载体，通过调控与操纵自旋实现数据存储、逻辑运算、量子计算等.二维电子材料中的自旋电子学研究是目前自旋电子学研究中的一个新兴热点研究方向.例如，石墨烯的自旋-轨道相互作用非常小，同时还具有可调载流子浓度、超高的电子迁移率等性质，因此可以作为自旋电子学理想的应用材料.2007 年，Bart van Wees带领的团队首次对石墨烯室温自旋输运进行了研究[22].如果将石墨烯应用于自旋电子学领域，至关重要的是诱导使其产生磁矩.有研究表明石墨烯经过各种物理和化学的修饰，它的性质可以得到有效调控[23-26].因此人们希望通过对石墨烯等二维材料构造缺陷、掺杂或在其表面吸附原子等来获得可调的磁性.

近年来，在具有特殊对称性的晶体材料中出现了将布洛赫(Bloch)电子的能谷作为新颖自由度的系列研究.能谷一般指布洛赫电子能带的最高处或最低处，如果材料中存在一系列简并或者接近简并的能谷，那么只要它们能够被动态地极化和探测，原则上这些能谷就可以形成分立的自由度.从这个意义上讲，能谷指标可以被用来编码和操作信息，相关的领域被称为能谷电子学(Valleytronics).近年来，二维体系中的能谷电子学受到了很多关注，包括对称性破缺的石墨烯、单层过渡金属二硫化物(MX2，M=Mo，W；X=S，Se，Te 等)以及反铁磁锰硫族磷酸盐MnXP3(X=S，Se) 等[27-34].

环境和能源问题一直是社会热点问题，如何高效的利用太阳能这一清洁能源，是解决这一问题的重要研究课题.20 世纪 70 年代，日本科学家发现在紫外线照射下可以通过 n 型光催化剂使水被分解为氧气和氢气[35],光催化技术由此诞生.TiO2作为一种性能优异的半导体材料，在光催化应用等诸多方面有着可观的应用前景.2001 年 Asahi 等人[36]发现 TiO2掺杂 N 后能够提高光催化活性，并给出了判断掺杂结构的依据.此后，人们又陆续提出了多种TiO2改性方法，如离子掺杂、半导体复合、贵金属沉积和光敏化等.除了掺杂以外，对于提升二维材料的光学性质，人们也可以通过制造缺陷和搭建异质结的方法来实现.

本文将对二维材料电子结构及其性能调控的研究进展作简单介绍.具体内容包括：第一性原理基础知识；二维材料自旋极化及能谷极化性质；二维材料及其异质结构的光学性质；吸附分子、引入掺杂和缺陷、加入应变及外场、搭建异质结等对二维材料性质的有效调控等.

2 研究方法

密度泛函理论作为一种计算手段，在众多科研领域得到了广泛的应用，尤其在物理、化学、材料科学等领域.用密度泛函理论可以模拟一些实验上难以进行甚至无法进行的研究工作，例如异质催化合成氨、少量杂质引起的金属脆化、行星形成时的材料性质等[37].

根据量子力学原理，研究由原子核和电子构成的多粒子体系性质时需要求解多粒子体系的薛定谔方程[38].研究多粒子体系，首先要进行Born-Oppenheimer 近似把原子核与电子的运动区分开来，这称为绝热近似[39].体系的薛定谔方程如下

(1)

括号中的三项分别为每个电子的动能，每个电子与所有原子核之间的作用能，不同电子之间的作用能.ψ=ψ(r1,…,rN)是电子波函数，E是电子的基态能量.可以把ψ表达为单个电子波函数的乘积，即ψ=ψ1(r)ψ2(r)…ψN(r)，该表达式称为Hartree乘积，这种近似即为单电子近似.即便如此，由于粒子数量太多，导致求解需要的计算量非常大，求解便成了一个很大的难题，密度泛函理论的出现解决了这一问题.

密度泛函理论的基石是Kohn和Hohenberg提出的两条基本原理.

原理一：从薛定谔方程得到的基态能量是电荷密度的唯一泛函.

有了这两条原理，接下来的任务就是找到能量泛函的表达式，以及如何得到真实的电荷密度.能量泛函可以表示为E[{ψi}]=Eknown[{ψi}]+EXC[{ψi}]，其中第一项的具体形式是已知的，第二项被称为交换关联项，它的具体形式人们不知道，只能采用一些近似的方法获得(如LDA,GGA近似等).即便如此，寻找真实电荷密度的计算量也十分巨大.于是Kohn和Sham提出了一套方程，称为Kohn - Sham 方程，具体形式如下

(2)

由于要求解的电荷密度包含在势能项中，因此需要用迭代计算的方式[38].目前最流行的模拟计算材料性质的软件包之一的VASP(Vienna Ab-initio Simulation Package)就是采用了迭代计算的方法，其计算流程如图2所示.

3 二维材料自旋极化性质.

基于大量的计算研究证明，通过将有机分子或者磁性过渡金属吸附到二维材料表面，以及将过渡金属掺杂到二维材料晶体结构当中，可以有效地产生自旋极化效应.在二维材料大家庭中，人们感兴趣的是上述所提到的石墨烯.石墨烯优异的二维薄膜状结构可以使其表面与被吸附物之间的相互作用最大化，而且还会引起其导电性产生显著的变化，因此以石墨烯为基底的纳米材料被广泛应用于各种类型的传感设备中.针对石墨烯单层晶体材料在自旋电子学领域的应用前景，人们研究了石墨烯吸附不同分子后的电子结构和掺杂过渡金属元素后的石墨烯吸附有机分子的自旋极化性质.

计算结果表明，将thiophene分子吸附到Zigzag型graphene纳米带边缘后thiophene分子会产生自旋极化.图3为吸附系统的自旋密度分布图及态密度图，从自旋密度分布图中可以看出系统产生了明显的自旋极化.图3中还可以看出整个吸附系统的态密度在费米能级附近是自旋劈裂的，说明此时系统是自旋极化的.我们知道，单独的thiophene分子的态密度是自旋简并的，但是从图3给出的吸附在graphene纳米带边缘后thiophene分子的态密度可以看出在费米能级附近出现了明显的自旋劈裂，此时thiophene分子产生了自旋极化，说明graphene纳米带可以对thiophene分子产生自旋注入，使得噻吩分子产生自旋极化[40].

图2 VASP计算流程图

图3 graphene纳米带吸附thiophene分子的自旋密度分布图和态密度图

人们研究了PdSe2中过渡金属原子掺杂导致的自旋极化效应，如图4所示.研究发现，当在PdSe2中掺杂Cr, Mn, Fe，Co时，PdSe2的带隙会明显减小.体系的投影态密度显示，掺杂原子和PdSe2的p-d轨道耦合对导致系统中费米能级附近杂质态的出现.从体系的磁矩、自旋密度分布、电荷转移的计算结果发现， Cr掺杂 PdSe2具有最大的自旋极化率[41].

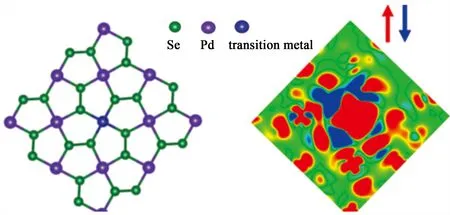
图4 过渡金属掺杂导致PdSe2产生自旋极化

掺杂graphene吸附小分子后电子结构将发生很大的变化.人们分别计算了N、Al元素掺杂graphene吸附CHCl3分子情况，如图5所示.对不同的吸附结构进行优化后发现，纯graphene和N掺杂graphene吸附CHCl3分子后吸附结构并没有发生明显的变化，而掺杂Al原子的graphene吸附CHCl3分子后系统发生了明显变化.通过计算不同吸附系统的形成能、净电荷转移、能带结构、态密度和差分电荷密度发现，掺入Al的graphene可以增强graphene与CHCl3分子彼此间的作用，Al 掺杂的graphene可以用来作为探测CHCl3分子的传感器材料[42].

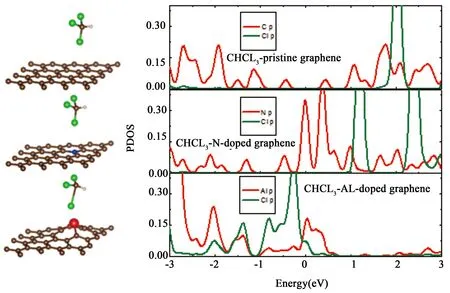
图5 CHCl3在不同掺杂graphene表面吸附结构图及态密度图

当过渡金属元素掺杂到graphene内部并吸附分子后可获得自旋极化效应.人们计算了吸附在掺杂过渡金属Mn、Cr、Fe、Co、Ni的graphene表面的benzene分子的自旋极化性质.如图6所示，由吸附前后benzene分子的投影态密度发现，苯分子吸附在掺杂 Mn 和Cr 原子的graphene表面时会出现明显的自旋极化.比较两种不同结构的电荷转移、形成能、吸附距离、自旋密度分布及差分电荷密度分布发现，benzene分子和掺入 Mn的graphene之间的相互作用更强，Mn原子掺杂的graphene可以诱导benzene分子产生更大的自旋极化[43].

图6 掺杂过渡金属的graphene吸附benzene分子的结构图及投影态密度图

有机非磁的benzene/Cu界面在电场控制下也可以获得良好的自发自旋极化性质.人们采用benzene/Cu (100)界面作为理论模型去研究有机磁场效应，如图7所示.通过改变Z轴方向上施加的电场值，人们可以研究外场对界面自发自旋极化的影响.计算发现，随着电场的增加，超过一定的阈值电场之后有机非磁的benzene/Cu界面费米面附近的自旋极化率出现震荡现象.通过分析体系的投影态密度可以发现，施加电场以后产生的电荷转移引起了分子与电极的p-d轨道耦合，使得界面发生自旋极化，这些现象并不是随着电场单调变化的，因此可以通过施加外加电场及改变吸附构型来实现有机非磁界面自发自旋极化的有效调控.

图7 benzene/Cu (100)面的吸附构型及自旋极化率随电场变化关系

通过选取不同的有机分子吸附在相同的电极表面，发现分子的选择对界面自旋极化性质具有重要的作用.通过改变有机分子在电极表面的吸附位置可以获得不同的界面自旋极化效应.相同的有机分子吸附在不同电极表面时界面自旋极化性质也是不一样的，如图8所示.因此人们也可以通过选择不同电极来改善界面的自旋极化，从而获得比较大的注入效率[44].

图8 不同吸附构型不同电场下benzene /Cu(100)系统自旋密度分布图

人们也计算了过渡金属掺杂的MoSeTe单层的电子结构和自旋极化特性，发现自旋极化出现在V、Mn、Fe、Co和Ni掺杂的MoSeTe中，并且Co掺杂的系统具有最大的自旋极化，而Cr掺杂的体系没有产生自旋极化特性.由于过渡金属掺杂的影响，体系的整个带隙显著改变.由过渡金属掺杂所引起的在费米能级附近的带隙中会产生新的自旋杂质态，而对于V、Mn、Fe、Co、Ni掺杂系统，电子自旋向上和向下态并不会消除.由图9可知，通过分析投影态密度，杂质能级的自旋态来自过渡金属原子与MoSeTe系统之间的强p-d轨道杂化.在过渡金属掺杂之后发生电荷转移，这些转移的电荷将填充自旋分裂的各个状态，因此导致过渡金属掺杂的MoSeTe体系发生自旋极化.此外，不同MoSeTe系统的自旋电荷密度分布也证实了过渡金属掺杂可以在MoSeTe中引起自旋极化.计算结果表明，过渡金属原子掺杂是一种调节MoSeTe自旋极化特性的有效方法，在基于二维材料的自旋电子器件中具有广阔的应用前景[45].

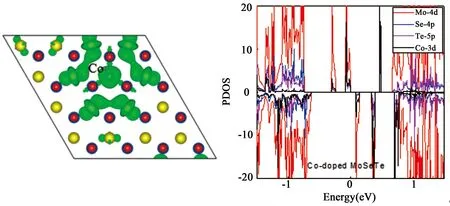
图9 Co掺杂MoSeTe结构图及投影态密度图

4 二维材料中的能谷极化效应

二维材料在谷电子学中也有重要的应用前景.能谷是与电子自旋自由度相类似的全新自由度，它可以提供新一代的信息储存方法以及作为半导体科技的载体.谷电子学中当前面临的主要挑战是在如何二维材料中获得谷自由度.基于此，人们从理论上通过在具有特定结构的二维材料中引入掺杂、吸附以及搭建异质结的方式来激发它的谷自由度，这为二维材料在谷电子学领域中的实际应用提供可靠的理论支持.

过渡金属元素掺杂和吸附可在二维WSSe中产生谷极化.掺杂原子V产生的杂质能级与WSSe的最高价带之间存在较强杂化，这导致V原子掺杂可以产生最大的谷极化，而Cr、Mn、Fe和Co原子掺杂只能引起极小的谷劈裂.除此之外，以Cr原子吸附为例，人们还计算了过渡金属元素吸附对谷自由度性质的影响，结果表明过渡金属元素吸附也可以引起WSSe中的谷极化.有趣的是，Cr原子与S原子之间的相互作用比Cr原子与Se原子之间的相互作用相对较强，因此在Cr-S系统中并未发生谷极化现象，并且当Cr原子吸附在Se表面上时可以获得最大的谷极化效应，如图10所示.诱导和控制WSSe的谷极化具有重大意义和挑战，这些工作提供了几种探索WSSe谷自由度的有效方法[46].

图10 WSSe中掺杂或吸附过渡金属原子导致谷极化

人们还研究了过渡金属元素掺杂的WTe2在应力应变调控下的谷极化特性.计算发现，当考虑到自旋轨道耦合效应时，只有在Co掺杂的WTe2中才会出现比较大的谷极化，可以实现反常谷霍尔效应.值得一提的是，应力作用可以适当地调节K和K'谷从而使谷极化大大增强.此外，在张力应变下的共掺杂WTe2中，在价带顶和导带低中都观察到了谷极化，如图11所示，这是WTe2相对于先前可以实现谷极化的二维过渡金属硫化物半导体的优势.这意味着可以根据上述共掺杂的WTe2中特殊的谷极化特性，设计出一种高效、低能耗的新型自旋能谷霍尔器件[47].

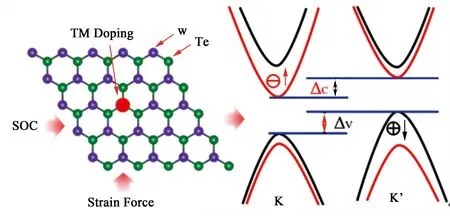
图11 WTe2中自旋轨道相互作用、过渡金属掺杂、施加应力等产生谷极化

5 二维材料及其异质结构的光学性质

人们研究了3d过渡金属元素Cu掺杂和Cu-N协同掺杂锐钛矿相 TiO2(101)面和(110)面体系的几何结构、体系稳定性及其电子性质，发现Cu-N 杂质对掺杂相较于 Cu 单掺杂体系更有助于防止电子空穴对的复合，更有利于体系光催化活性的提高.人们还计算了Cu在TiO2(101)面和(110)面上发生的替位、空隙、吸附等掺杂方式的缺陷形成能，从而得到掺杂体系相对最稳定的结构，发现Cu原子掺入时易出现在晶体(001)面上，在此基础之上掺入的N原子易替代位于Cu原子水平方向的O位.此外，又分别计算了纯净TiO2、Cu-TiO2和Cu-N协同掺杂TiO2后体系的电子结构，发现掺杂结构带隙减小，禁带中均出现了杂质态，同时也发现共掺杂体系的带隙缩短程度大于单掺杂体系，同时共掺杂分别引入了占据态和未占据态，位于带隙中捕获空穴和电子，进而提高了光催化活性，并使半导体性TiO2体系向半金属性发生转变.除了磁性过渡金属对TiO2表面态的影响，人们还研究了电子补偿对共掺杂锐钛矿相TiO2的电子结构及相关性质.计算得出了一系列非金属元素(N、S、P、F)以及过渡金属元素(Zr、Nb、V)单掺杂对TiO2的晶体结构、电子性质及带边位置以及差分电荷密度分布等的影响，如图12所示.计算结果表明掺杂原子与TiO2发生p-d轨道杂化效应，禁带中新电子态的出现有利于光生电子-空穴对的分离，同时带边位置发生了明显变化，如图13所示，其中F、S、Nb 和Zr掺杂TiO2体系的氧化还原能力增强.

图12 掺杂TiO2的带边位置

为了研究遵守电荷补偿原则的施主受主杂质共掺杂对扩展TiO2材料光谱吸收范围的影响，人们还讨论了(P+Nb)、(S+Zr)和(N+V)电荷补偿对共掺杂TiO2体系的结合能和电子结构，如图13所示，并与n型的(F+V)共掺TiO2做了对比，发现电荷补偿对共掺TiO2体系的带隙变的更窄，吸收带边发生了红移，这对体系吸收可见光提高光催化效率是有利的[48].

在二维材料中引入缺陷的方式也可以增强单层或异质结结构的光学性质.人们研究了在PdSe2晶体结构中引入Pd和Se原子缺陷对光学性质的增强效果.如图14所示，通过计算能带结构发现，在引入Pd或Se原子缺陷后能带中出现了新的中间能隙状态，体系带隙减小了.同时，由于Pd或Se原子缺陷引起的新的中间能隙态的出现可以在低光子能量区域观察到介电常数和吸收光谱的明显峰值，并且保留了突出的晶体结构各向异性的特征，如图14所示.与原始的PdSe2相比，引入Pd或Se缺陷后，可见光区域的吸收面积变宽.能带中间能隙态的出现会带来新的吸收峰，从而激活光谱中产生更多新的光学跃迁效果.对于引入原子缺陷前后的光学折射率和反射率也发现产生了类似的变化.此外，人们可以通过分析电子能量损失谱的差异用来识别不同的缺陷.所有这些发现为调控单层PdSe2的电子和光学特性提供了有效的手段，并为单层PdSe2晶体材料在光电应用中提供了可能[49].

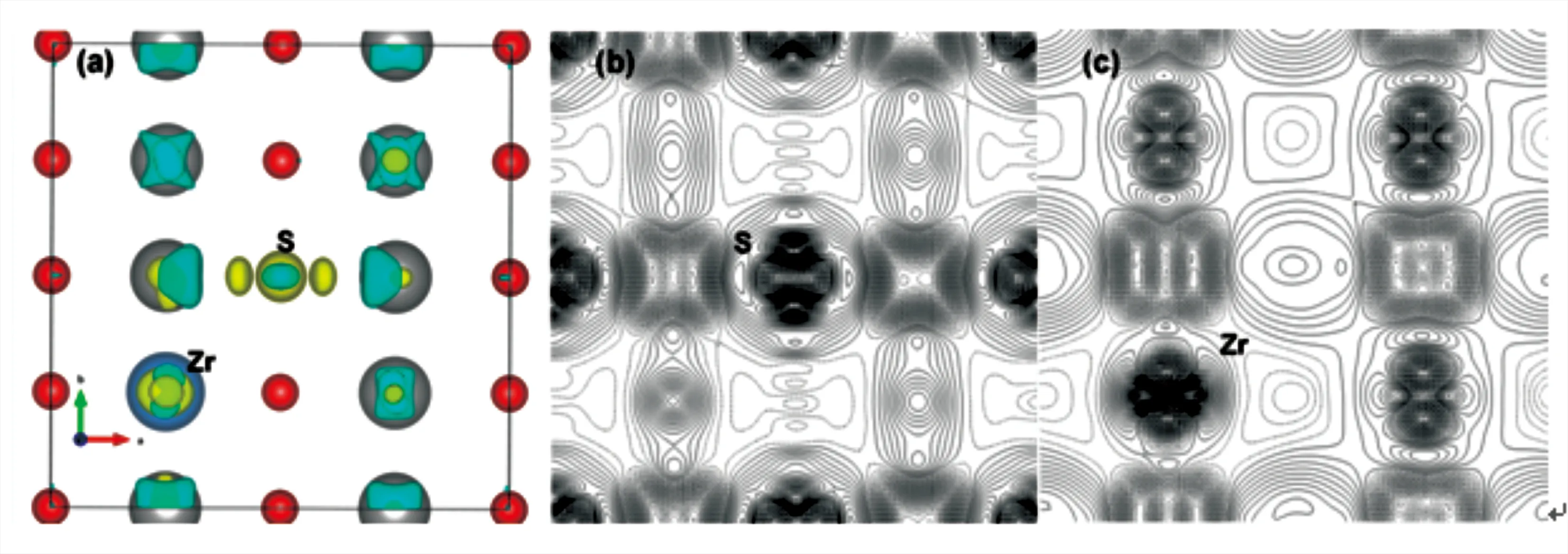
图13 (S+Zr)共掺TiO2电荷密度分布图

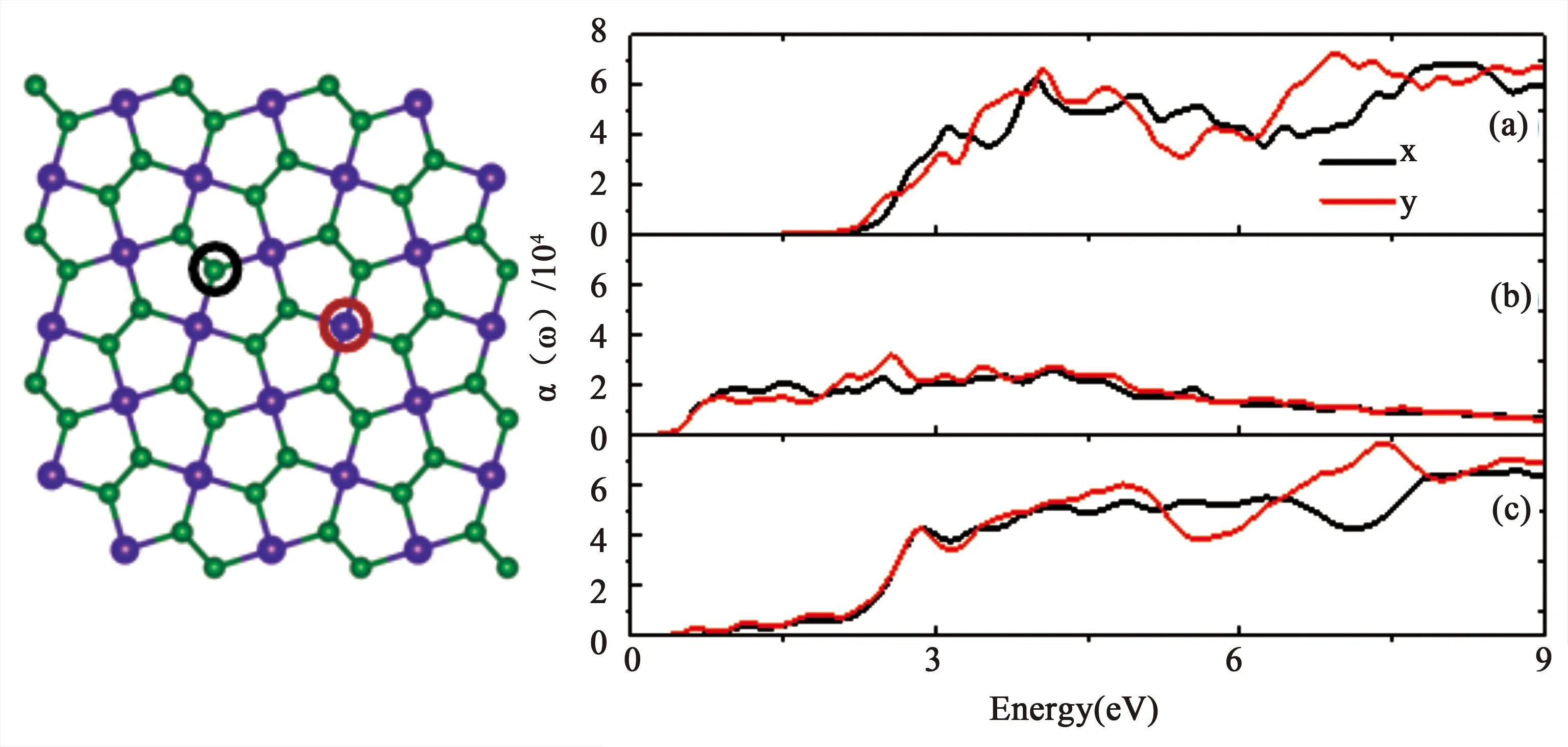
图14 PdSe2结构图及光吸收常数图

图15 graphene/MoS2异质结结构能带结构和能量损失谱

单层二维材料的一些性质可以通过搭建形成异质结结构来提高，比如二维材料具有较为良好的光学性质，在光水解、催化合成氢等方面有着良好的应用，将结构相近、尺度相似以及晶格匹配度高的其他二维材料与其匹配为异质结结构，可以优化、提高其主要在可见光范围内的光吸收谱，获得更为优异的光学性质.基于这一点，人们挑选了几种合适的二维材料如graphene与MoS2构建成为异质结结构，如图15所示.与单层graphene和MoS2体系相比，graphene/MoS2体系的光学性质明显得到了提高.对于graphene/MoS2体系，整个带隙和介电常数变大，并且体系的吸收系数、折射率和反射率光谱存在红移，能量损失谱发生了蓝移.以上所有结果表明，由于异质结的形成，与单层结构相比，graphene/MoS2系统的光学性能得到了显着改善，这为二维材料在光学应用领域中提供了有效的方法[50].

在Graphene与WSe2体系中，人们采用引入W和Se原子缺陷的方式来研究其对整个体系光学性质的影响.研究发现搭建成为异质结结构之后整个体系的光学性质明显增强.引入W和Se原子缺陷后，整体结构的光学性质得到明显加强，各方向的光谱发生了不同程度的红移.同时研究发现引入W原子缺陷所产生的效果要大于引入Se原子缺陷所产生的效果，这对于二维材料表征光学性质提供了一项有益的手段[51].

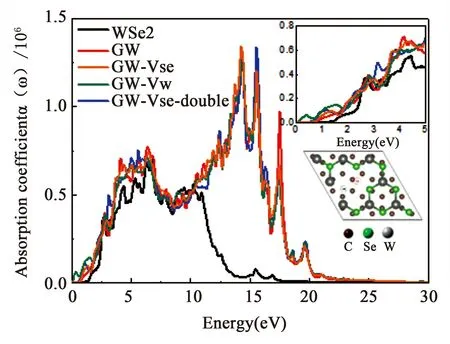
图16 空位对Graphene/WSe2异质结构光学性质的影响

6 结 语

基于密度泛函理论，通过第一性原理计算的手段，人们研究了在二维材料中通过掺杂不同元素或吸附有机分子实现的自旋极化效应.除此之外，人们发现在某些高对称的二维材料中可以通过引入掺杂或施加应力等方式实现能谷极化并对其进行有效调控.另一方面，计算发现通过搭建异质结的方式可以有效提高二维材料的光学性能.吸附分子、引入掺杂和缺陷、加入应变及外场、搭建异质结等可对二维材料电子结构实现有效调控，这对拓宽二维材料研究领域及实现其在光、电、磁等领域的实际应用具有重要推动作用.