型线参数对双涡圈涡旋压缩机性能的影响
2020-10-16张有彪张朋成张宇波
彭 斌, 张有彪, 张朋成, 张宇波, 尹 贝
(兰州理工大学 机电工程学院, 甘肃 兰州 730050)
引言
由于双涡圈涡旋压缩机更适用于大排气量和大功率场合,因而引起广泛的研究。顾兆林等[1]提出了双涡圈及多涡圈的几何理论以及基本结构参数计算方法,通过对比单涡圈与双涡圈的容积特性,得出了多涡圈不仅可以减小回转半径,而且可以降低滑动面摩擦速度进而减小磨损;王君等[2]建立了适用于任意齿数的涡旋盘通用几何模型,深入研究了涡旋齿数对压缩机性能的影响,丰富了多涡圈涡旋压缩机理论;梁高林等[3]建立了无油双涡圈压缩机的泄漏模型,并定量分析了泄漏线长度、泄漏量的变化情况;彭斌等[4]对新型无油涡旋压缩机的泄漏特性进行了深入研究;许多学者对涡旋压缩机的几何模型以及数学模型进行了深入研究[5-7];刘国平等[8]建立了一种对涡旋压缩机动涡旋盘进行动态温度场仿真的分析方法,并得出了涡旋盘上的温度变化规律;赵嫚[9]对双涡圈涡旋压缩机的动力学特性进行研究;邓亦攀等[10]对微型高压压缩机效率进行数值分析;侯才生等[11]详细分析了影响变截面涡旋压缩机齿厚的因素,并精确建立了齿厚与型线参数之间的关系; 王训杰等[12]提出了一种基于动涡旋盘气体力分析的结构参数设计方法。尽管关于双涡圈的文献较多,但关于双涡齿基圆半径和渐开线发生角对双涡圈涡旋压缩机性能的影响研究较少。本研究着重研究基圆半径和渐开线发生角对双涡齿涡旋压缩机性能的影响。
1 双涡圈涡旋盘的几何模型
1.1 双涡旋齿的形成
如图1所示,圆渐开线双涡齿静涡旋盘是2条由基圆处发生并且相位角相差180°的涡旋体组成,2条涡旋齿旋转90°后可形成动涡旋盘涡旋齿,动静涡旋盘偏移一定距离安装就可以形成能够正确啮合的工作腔体,如图2所示。单涡圈涡旋压缩机在工作时,形成2组对称的工作腔,对称腔体同时完成吸气、压缩和排气过程。由于双涡圈涡旋齿结构的特殊性,主轴回转1周,依次形成相位相差90°的4组工作腔,4组工作腔依次完成吸气、压缩和排气过程。双涡圈涡旋齿基本几何参数计算方法如下。

图1 静涡齿示意图

图2 动静涡旋盘啮合
涡旋齿节距pt:
pt=πa
(1)
涡旋齿齿厚t:
t=2aα
(2)
动静盘啮合回转半径Ror:
(3)
式中,a——基圆半径,rad
α——渐开线起始角,rad
1.2 双涡圈加工过程中刀具与涡旋齿的干涉
图3为铣刀加工双涡圈涡旋齿示意图,与加工单涡圈涡旋齿相同,在加工双涡齿时,铣刀中心起落点在基圆上,刀具最大直径φmax为:
φmax=pt-t=πa-2aα
(4)
在未对双涡圈齿头型线进行修正之前,双涡圈的排气角取决于铣刀与涡旋齿的干涉,因此,求解出干涉点对应的渐开角对研究压缩机排气过程至关重要。如图3所示,A1,A2分别为双涡齿外侧型线的干涉点,在该直角坐标系下,刀具圆的方程为:

图3 刀具与涡旋齿干涉
(5)
双涡圈外侧型线方程为:
(6)
将涡旋齿外侧型线方程带入刀具圆方程中得:
(7)
(8)
从吸气腔吸气结束到排气腔刚开始排气瞬间,主轴回转角为θD:
θD=φE-φD
(9)
式中,φE为双涡齿中心渐开面最终展角,rad。
(10)
θD=φE-φD
(11)
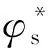
(12)
1.3 双涡圈各工作腔容积
1) 圆渐开线型线的几何理论
如图4所示,圆渐开线DP基圆半径为a,取DP上一点B,其展角为φ,渐开线弧长为L,发生线长为l,当展开角有一定增量dφ时,其发生线的增量为dl,圆渐开线弧长增量为dL,对应面积的增量为dS,将圆渐开线、基圆和发生线所围成的面积记作S。
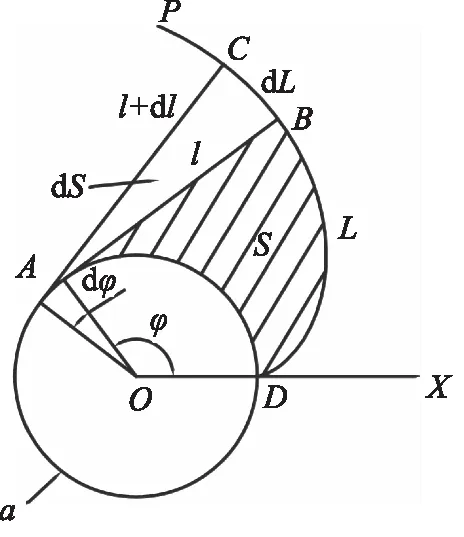
图4 圆渐开线
由渐开线的性质知:
微元三角形的面积dS为:
(13)
则阴影部分的面积S为:
(14)
2) 工作腔容积
图2所示为主轴转角为0时动静涡旋齿啮合示意图,图中阴影部分的面积计算公式如下:
Si=S内-S外
(15)
(16)
式中,i=1,2,3,…,n。
吸气容积:
=Hpt(pt-2t)(4φe-5π)
(17)
排气容积:
=Hpt(pt-2t)(4φs+5π)
(18)
式中,H为涡旋齿高度,mm。
1.4 双涡圈压缩机的泄漏
双涡圈涡旋压缩机在工作过程中的泄漏形式主要有2种:通过涡旋齿轴向间隙的径向泄漏和通过涡旋齿径向间隙的切向泄漏。切向泄漏线长度等于涡旋齿的齿高,径向泄漏模型如图5所示,径向泄漏线可以分为两部分:向外泄漏线LAC,LAD和向内泄漏线LBC,LBD,各径向泄漏线长度为:

图5 径向泄漏模型
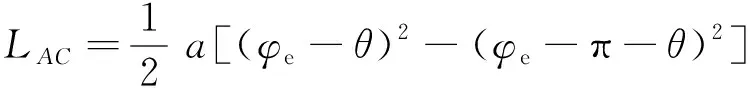
(19)
(20)
(21)
(22)
式中,φe为中心面渐开线最终展角,rad。
2 渐开线发生角对双涡圈压缩机性能的影响
2.1 渐开线发生角的取值范围
本研究中对某一厂家生产的双涡圈涡旋压缩机进行理论研究,其参数如表1所示。

表1 涡旋盘基本参数
当基圆半径为定值而发生角发生变化时,若想要形成能够正确啮合的双涡旋齿,需要对发生角的范围做进一步研究。涡旋齿在加工时, 铣刀最大直径φmax的取值为:
φmax=pt-t=πa-2aα
(23)
齿数为Z的多涡旋齿若要形成能够正确啮合的型线,则齿数Z应满足:
Z<π/2(α)
(24)
查询机械手册可知,铣刀最小直径为0.5 mm,若要使式(1)中φmax有实际工程意义,则需:
φmax≥0.5
(25)
联立式(23)~式(25)可得。
在基圆半径已知时,若要构成能正确啮合的双涡齿型线,发生角α需满足以下条件:
(26)
由式(26)可知,当双涡齿基圆半径为a=9.231 mm时,构成能正确啮合型线的发生角α的取值范围为:
(27)
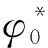
分析模型的齿头修正采用直接截断修正,并且在齿头修正以后涡旋齿中心渐开面的起始角为φs,由式(10)及式(11)得,采用直接截断修正后双涡圈涡旋压缩机的排气角θD变小。由式(18)得,采用直接截断修正后双涡圈涡旋压缩机的排气容积变大,排气压力变小;采用直接截断修正后双涡圈涡旋压缩机的内容积比变小,内压力比变小[13]。
2.2 渐开线发生角对压缩机基本几何参数的影响
运用推导得出的公式以及结论,在MATLAB中编程并作图,得渐开线发生角发生变化时压缩机基本参数变化的变化线图,如图6、图7所示。由图6、图7可知,在基圆半径a不变的情况下,随着渐开线发生角α的逐渐增大,双涡圈涡旋齿壁厚以线性增长趋势逐渐增大,主轴回转半径、吸气容积和排气容积以线性下降趋势逐渐减小。
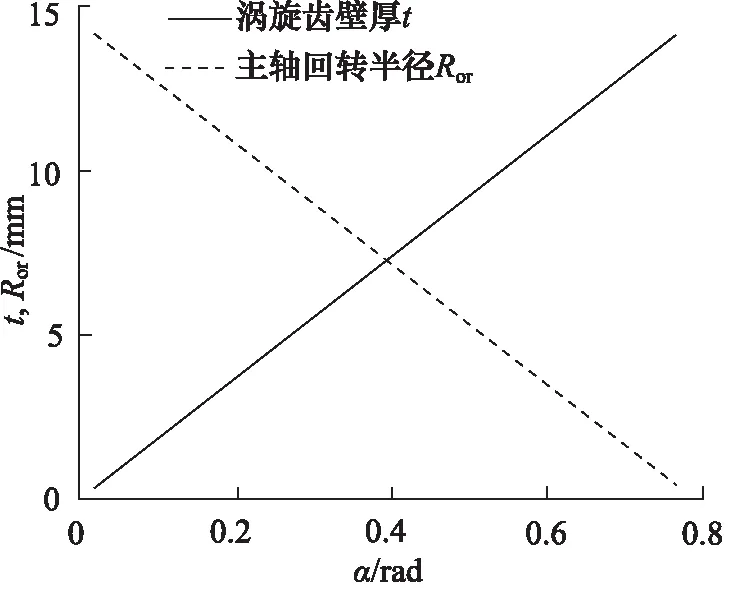
图6 t, Ror随α的变化情况

图7 吸气、排气容积随α的变化情况
3 基圆半径a对压缩机性能的影响
基圆半径对参数的影响如图8、图9所示,由图8、图9可知:当渐开线发生角α取定值时,随着基圆半径a逐渐增大,双涡圈涡旋齿的节距、齿厚和回转半径线性逐渐增大,吸气容积和排气容积非线性增大。径向泄漏线长度随主轴转角变化规律如图10所示,由图10可以直观地看出4条径向泄漏线的长度以及总泄漏线长度与主轴转角成线性关系,且随着基圆半径的逐渐增大,径向泄漏线长度线性增大。

图8 基圆半径对基本参数的影响
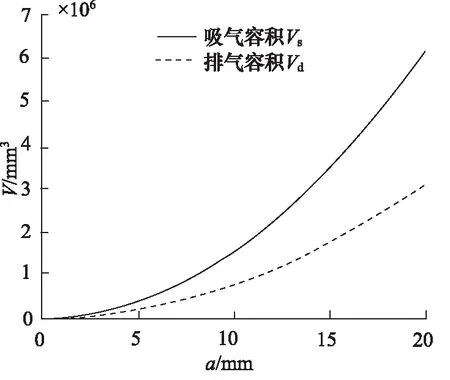
图9 基圆半径对吸气、排气容积的影响

图10 径向泄漏线长度随主轴转角变化规律
4 结论
(1) 推导出了在基圆半径不变的情况下,要形成能正确啮合的双涡旋体的涡旋型线起始角的取值范围;
(2) 在圆渐开线起始角不变的情况下,基圆半径与双涡圈涡旋齿的节距、壁厚,径向泄漏线长度和主轴回转半径成正比;随着基圆半径的增大,吸气容积、排气容积逐渐增大,但与基圆半径成非线性关系;
(3) 在基圆半径不变的情况下,双涡圈涡旋齿渐开线发生角与涡旋齿壁厚、吸气容积和排气容积成正比,与主轴回转半径成反比。
