液压作动系统的传感器故障检测设计

窦海斌, 文国兴

(1.滨州学院 机电工程学院， 山东 滨州 256600；2.滨州学院 理学院， 山东 滨州 256600)

引言

液压作动系统在人们的生产和生活中有着广泛的应用，常见的应用包括同步举升系统[1]、大型客机的非相似冗余作动系统[2]以及负载模拟器[3]等，保证液压作动系统能够有效的工作是十分必要的。在液压系统中常见的故障有4类，分别是：液压泵失效，液压泵和液压执行元件的泄漏，传感器线路的老化和故障，油液污染[4]。本研究将液压作动系统的传感器故障作为研究对象，传感器故障通常是一种慢变的故障，起始时往往不被注意并且通常会被系统的扰动所覆盖，因此增加了故障检测的难度。

目前虽然有一些学者对传感器的故障检测进行了研究但仍然有一些不足。比如所用的方法只允许一个故障发生，不能处理多故障的情况；对于非线性系统的传感器故障而言，需要提前知道Lipschitz常数，而Lipschitz常数的获得通常是比较难的，特别是对于液压系统而言。以上问题限制了这些方法的应用，本研究提出了一种传感器故障的检测方法，能够克服以上的缺陷。首先利用模型转换实现了系统不确定项与传感器故障的解耦，得到了2个子系统。针对2个子系统分别设计了滑模观测器和Luenberger观测器，利用滑模观测器消除扰动，利用Luenberger观测器使观测器的评估误差趋于0。滑模理论被认为是一种有效的控制方法来处理系统的扰动问题。当该理论用于设计观测器时，能够保证偏差动态的轨迹保持在滑模面上而不受外部扰动的影响，从而保证了观测器能够可靠的观测所需变量。Luenberger观测器是一种传统的观测器，它的原理是根据系统的输入和输出关系建立观测器模型，然后取观测器的输出与估计做比较，最终使得稳态误差为0来保证观测器的稳定。对于Luenberger观测器的详细介绍请参阅文献[5]。

本研究的设计方法能够实现多个传感器故障的检测，而不必假设每次只有一个故障发生；在Lipschitz常数未知的情况下能够基于非线性模型实现传感器故障的有效检测。

1 液压作动系统的建模与模型转换

1.1 液压系统建模

液压系统如图1所示，该系统主要包括了1个液压缸和1个伺服阀。下面将针对该液压作动系统进行数学建模。对于伺服阀而言，滑阀阀芯位移xv与控制输入u相关，并且可以表示成一阶模型的形式[6]：

图1 液压作动系统的原理图

(1)

式中，τv——时间常数

kv——伺服阀增益

用qh表示负载流量，负载流量关于xv和负载压力ph的表达式为[7]：

(2)

式中，Cd——伺服阀的流量系数

ω——伺服阀的阀口面积梯度

ps——供油压力

压力动态模型可表示为[3]：

(3)

式中，βe——油液弹性模量

Vt——液压缸及其余伺服阀管路的总容积

A——活塞面积

Ctm——总的泄漏系数

xc——液压缸的位移

ph——负载压力

由作动器的受力可得：

(4)

式中，m——负载的质量

Bh——黏性摩擦系数

Ff——系统不确定性和扰动

联合方程式(1)～式(4)得模型为：

其中，Δψ(t)=Ff。在不考虑传感器故障时，模型的抽象形式为：

(5)

1.2 模型转换

考虑传感器故障的情况下，可得:

(6)

推论1：非线性项f(x,t)满足Lipschitz条件为，该条件可通过文献[8]获得。

其中，Lf为Lipschitz常数并且假设为未知量。

假设1：函数Δψ(t)未知且有上界，即满足||Δψ(t)||≤ρd。传感器故障fs满足||fs||≤ρs。

推论2：rank(E)=1,并且rank(CE)=rank(E)

推论2可通过简单的计算获得。如果推论2成立，则存在状态和输出转换为：

(7)

其中，z1∈R1，z2∈R3×1，η1∈R1andη2∈R2×1， 并且:

其中,T∈R4×4，A11∈R1，A22∈R3×3。

其中，B1∈R1

其中，E1∈R1

其中，C11∈R1，C22∈R2×3，S∈R3×3

其中，D2∈R2×2。

利用T和S2个矩阵可将初始系统转换为2个子系统式(8)和式(9)：

(8)

(9)

通过观察式(8)和式(9)可得初始系统实现了传感器故障和系统不确定性的完全解耦。下一步引入1个新的状态。定义z3为：

(10)

对式(10)进行微分得：

(11)

利用式(9)和式(11)可得：

(12)

增广系统式(12)可化成抽象形式为：

(13)

子系统式(8)可以写为：

(14)

推论3：有非负实部复数s满足下式：

(15)

其中，n=4。推论3为最小相位条件，可通过简单的计算获得。

引理1：如果推论3成立，则(A0,C0)可观测，即存在矩阵L0∈R5×2使得A0-L0C0稳定，并且对任意Q0>0以下方程：

(A0-L0C0)TP0+P0(A0-L0C0)=-Q0

(16)

有唯一解P0。引理1的证明可参考文献[9]。

2 传感器故障的检测

基于子系统式(14)，滑模观测器设计为：

(17)

(18)

(19)

其中，lk1是正常数。

对子系统式(13)，一种Luenberger观测器设计为：

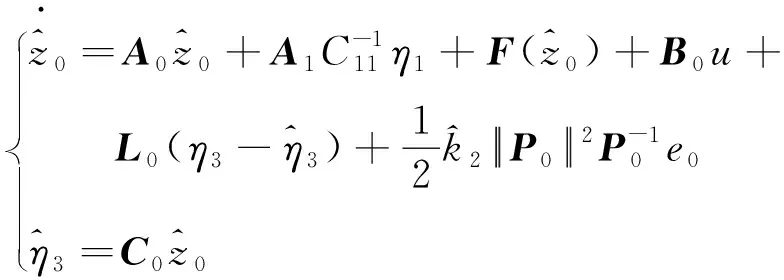
(20)

(21)

其中，lk2是正常数。联立式(13)、式(14)、式(17)、式(20)得误差动态方程为：

(22)

(23)

(24)

证明：构造Lyapunov函数：

V(t)=V1(t)+V0(t)+V2(t)+V3(t)

由推论1可得：

Lf||T-1|||e0||

通过一个简单的计算可得：

其中，Lf1=||T1||Lf，Lf2=||T2||Lf。

对V1(t)求微分可得：

(25)

使用不等式2XTY≤(1/α)XTX+αYTY，其中α>0，于是可得：

(26)

(27)

(28)

对V0(t)求时间微分可得：

(29)

使用不等式2XTY≤(1/α)XTX+αYTY，则得到：

(30)

(31)

其中，V2(t)的时间微分为：

(32)

其中，V3的时间微分为：

(33)

使用式(28)、式(31)、式(32)和式(33)可得：

(34)

不等式(34)暗示了评估误差e1和e0能够渐进收敛到0。

证毕。

推论4：如果l1满足如下要求：

l1≥(||A2||+Lf1||T-1||)||e0||+γ1

(35)

其中，γ1为一个正的标量。

则误差动态式(22)能够到达滑模面：

S={(e1,e0)|e1=0}

证明：构造Lyapunov函数:

对V1进行时间微分可得：

(36)

由式(36)可得：

(37)

由式(37)可得到达条件是满足的[10]。

证毕。

如果在模型中考虑了传感器故障，则式(22)和式(23)变为：

(38)

(39)

3 仿真

为了验证提出方法的有效性，以液压系统为例进行仿真。仿真参数[11-13]如表1所示。

表1 仿真参数[11-13]

在仿真过程中假设只有液压缸的位移和液压缸的负载压力是被测量。位置传感器故障用fs1表示，压力传感器故障用fs2表示。系统的不确定性假设为Δψ=100+200sin(πt)N。转换矩阵设计为：

不等式(24)可转换为以下线性矩阵不等式的可行性问题，即存在矩阵P1>0,P01>0,P02>0,X,Y01,Y02使以下的不等式成立：

(40)

利用MATLAB的LMI工具箱解线性不等式(40)可得:

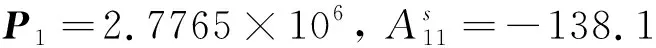
下面通过2个例子来验证提出方法的有效性。

示例1：假设位置传感器故障为：

假设压力传感器没有故障，即fs2=0,∀t。仿真曲线如图2所示。通过图2可知当传感器故障未发生时残差为0，一旦位置传感器故障发生，残差偏离0。当该残差超过阈值0.4时可得至少有1个传感器故障发生，传感器故障被成功检测到。

图2 示例1残差曲线

示例2：位置传感器故障和压力传感器故障分别假设为：

仿真曲线如图3所示。

图3 示例2残差曲线

通过图3可得残差曲线在10 s和15 s时偏离0，当残差超过0.4时说明故障发生，所以本研究提出的方法能够有效的检测多个传感器故障。

此外，仿真中所使用的阈值通过多次调试获得，因此需要提前获知故障的相关参数。如图2和图3所示，在初始阶段由于初值选择问题使残差超过了给定的阈值，从而会导致虚警的发生。为解决该问题可令系统开机一定时间之后再启动故障检测系统，通过一定的延时跳过虚警阶段，保证故障检测系统可靠的工作。

4 结论

针对液压作动系统的传感器故障检测开展研究工作。首先将液压初始模型分解为2个解耦的子模型，其中一个子模型只含系统的不确定性而另一个子模型只含传感器故障。针对这2个子模型分别设计了滑模观测器和Luenberger观测器。最后通过仿真验证了提出方法的有效性。