基于(2D)2-PCANet的种子图像识别

刘彩玲 岳荷荷

(山西农业大学软件学院 山西 太谷 030800)

0 引 言

将计算机视觉技术和农作物图像识别相结合可以减缓人工识别结果的主观性和提升识别的速度。图像的特征表示是识别的关键，常见的特征有图像的大小、颜色、形状、纹理等。采用PCA[1]、KPCA[2-3]等算法对图像矩阵降维后表示特征，这些特征都是低层特征，文献[4-7]研究者采用该方法对杂草种子图像进行识别，取得了较好的结果。组合低层特征形成较高层次的特征，即深度特征学习[8-10]，相比低层特征，大部分采用深度特征表示图像的方法有更好的识别率。提取图像高层特征的关键是特征提取网络中的特征模板。常见的深度学习神经网络有DNN[11]、CNN[12]、RNN[13]、GAN[14]等，而PCANet[15-19]是其中一种简单的特征提取CNN网络，其采用PCA算法计算特征模板，在杂草种子图像识别上取得了较好的识别率。LDA算法和KPCA算法都是比较常见的降维方法，但是LDA方法是有监督的降维方法，需要知道每一个训练样本的类别，而特征提取网络是将一个图像分割为多个分片，提取每一个分片的特征。因此考虑将同一类图像的所有分片作为一类，但是实验结果表明，采用LDA算法计算特征模板的识别率远不如PCA算法，所以将同一类图像的所有分片作为一类不合适。虽然KPCA算法考虑了图像的高阶相关性，但是由于一个图像会分割成大量的分片，导致计算量很大。

采用PCA等算法计算特征模板时，需先将二维图像表示为一维向量，然后计算协方差矩阵，并计算特征向量，这种方法不仅计算量很大，而且在计算相关性时可能会破坏图像的二维结构，丢失像素点行列之间的关系信息。而本文改进后的(2D)2-PCANet采用(2D)2-PCA[20]计算网络的特征模板。2DPCA[21-23]算法是直接对二维矩阵求协方差矩阵，然后计算特征向量进行特征提取的，不需要转换为一维向量后再计算协方差矩阵，不仅计算量小，而且相比PCA方法，保留了行列之间的相关性信息。但是2DPCA算法相比PCA需要更多的空间表示图像，因此图像识别速度较慢。本文采用(2D)2-PCA计算特征模板，先对行进行降维，再对列进行降维，相比2DPCA算法减少了所需空间，但也导致可能丢失更多图像信息。为了弥补减少输出个数、加快识别速度而降低的图像识别率，本文对计算出的特征模板进行特征训练，通过减小每一层图像的重构误差来进一步提高识别率。实验结果表明，相比PCANet，使用带特征训练的(2D)2-PCANet取得了较高的识别率。

本文实验采用的杂草种子图像数据集包括211个类别，共9 191幅彩色图像，每幅种子图像的大小为110×80像素。部分种子图像如图1所示。

图1 部分种子图像

1 特征网络

本文构建了两个两层特征提取网络PCANet和(2D)2-PCANet。首先采用PCA和2D2-PCA算法计算每层的特征模板，然后通过该层的输入和相应的特征模板做卷积即可得到每一层的输出，并将最后一层的输出二值化，减少图像表示特征的维数，最后将网络的输出输入到SVM分类器中进行图像识别。

1.1 PCA与2DPCA

PCA与2DPCA算法都是主要用于提取图像特征表示图像并进行图像识别的，本文将这两种算法分别用于两层网络的图像分片的特征提取中。设N个m×n图像矩阵Ii(i=1,2,…,N)是独立同分布的随机图像样本，它们的列拉直向量为ai(i=1,2,…,N)。

1.2 特征模板

1.2.1PCA特征模板

假定Ii∈Rm×n×3表示每幅彩色种子输入图像，为了构建两层卷积特征提取网络，首先需确定特征模板值，然后采用该模板和每幅输入图像做卷积得到输出。因此为了计算方便，在网络的第一层，首先将输入图像分割为大小为k1像素×k1像素×3通道有重叠的分片，为了将图像中所有的特征都提取出来，设分割步长为1，则每幅输入图像可分割为s1s2个有重叠的分片，其中，s1=m-k1+1，s2=n-k1+1。然后将每个图像分片去均值并表示成一个列向量ai,j∈R3k1k1，将每幅图像的所有分片向量表示成矩阵Ai=[ai,1,ai,2,…,ai,j,…,ai,s1s2]，其中ai,j表示图像i的第j个分片。假设训练集中有N幅种子图像，则训练集中所有图像的分片向量构成矩阵A=[A1,A2,…,AN]。

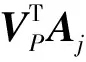
(1)

通过类似的方法计算该两层PCANet卷积网络模型中每层的特征提取模板。

1.2.2(2D)2-PCA特征模板

(2)

通过类似的方法计算两层卷积网络模型中每层的特征提取模板。

1.3 网络输出

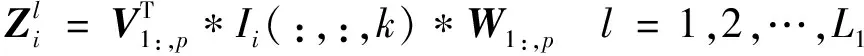
p=1,2,…,d1q=1,2,…,d2k=1,2,3

(3)

实验表明，对于彩色图像，如果对输出结果进行稀疏，即增强每幅图像中的明显特征，同时弱化图像中的不明显特征，可以提升图像的识别率。对每个输出结果采用式(4)进行稀疏处理，其中：sign()表示符号函数；max()表示求最大值函数；abs()表示求绝对值函数。

(4)

l=1,2,…,L2p=1,2,…,g1q=1,2,…,g2

k=1,2,…,U

(5)

(6)

(7)

对于Ii在第二层的R个输出，本文将每个输出分为B块，每块的大小为b1×b2。对于每个输出中的每块，计算十进制0至2L2-1的直方图，将每块化作长度为2L2的向量。然后将这B块对应的向量连接起来作为

(8)

1.4 特征训练

虽然特征网络在采用权值初始化方法初始化各层的权值后，不需要再增加权值训练即可取得较好的识别率，但是当网络的输出个数较少时会丢失部分主成分，而当网络的输出个数较多时，会增加表示图像特征向量的长度，从而增加分类的复杂性，并且图像的识别率不会随着输出数量的增加而一直增加。因此可以在保持输出个数一定的情况下，对网络的权值进行训练，提升图像识别率的同时，并且分类时间不长。

(9)

(10)

(11)

(12)

由于Yi是稀疏的，故本文采用Sparse Orthonormal Transforms(SOTs)[25]稀疏正交交换权值训练方法，其在满足输出矩阵稀疏的条件下，通过求使得迹最小的权值矩阵来训练权值。SOTs不仅所需的训练时间较短，并且不会随着训练集中样本的增加而占用更大的内存，占用内存的大小只与每个样本图像分片的大小有关，而与训练集中样本的数量无关。

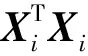
(13)

(14)

本文采用逐层训练方法，首先训练第一层的行列权值模板，然后固定第一层的模板。采用类似的方法训练第二层的权值。

1.5 分类器

本文将深度卷积网络的输出输入到SVM[26]分类器中，对杂草种子图像进行分类。杂草种子图像训练集中共包含N幅训练图像，经过两层(2D)2-PCANet后即可得到所有训练图像的特征表示，用矩阵F=[f1,f2,…,fN]∈RN×2L2UB表示。每幅图像都有确定的类别mi，若将所有图像的类别表示为一个向量M，则M=[m1,m2,…,mN]∈RN。根据任意两类种子图像的特征和类别，为它们构建一个SVM模型。对于测试数据集中的每幅图像，首先根据(2D)2-PCANet得到图像的特征表示，然后将其输入到每一个SVM模型中，得到该测试种子图像的可能类别。每个SVM模型会给出一个预测类别和预测概率，SVM分类器将最大概率的类别作为该测试种子图像的最终类别。

2 实 验

本文随机地将数据集分为训练数据集和测试数据集两部分，其中80%的种子图像，共7364幅图像作为训练数据，20%的种子图像，共1827幅图像作为测试数据。

对于本文设计的两种两层特征网络，第一层的特征数为18，第二层的特征数为9。对于(2D)2-PCANet第一层的18个输出，将第{x,x+6,x+12}(x=1,2,…,6)个输出作为第二层网络的一个输入；对于PCANet的第一层的18个输出，将第{(x-1)×3+1,(x-1)×3+2,(x-1)×3+3}(x=1,2,…,6)个输出作为第二层网络的一个输入。因此第二层共6个输出。如表1所示，通过实验比较(2D)2-PCANet在不同分片大小下的识别率可知，当k1=5,k2=7时识别率较高，为97.04%，由此网络得到的图像表示向量为138240维。

表1 不同分片的识别率

对于PCANet的第一层的18个特征模板，取PCA特征矩阵的前18个特征值较大的特征向量作为特征模板，每个特征模板是75维的向量，由于原始图像为彩色图像，因此可以将其表示成一个5×5×3的矩阵，每个5×5的矩阵用于提取1个颜色通道的特征。类似第一层计算特征模板的方法，可以计算出PCANet第二层的9个特征模板，每个特征模板是147维的向量，由于将第一层的每3个输出组合作为第二层的1个输入，因此将其表示成1个7×7×3的矩阵，分别用于每幅输入图像的特征提取。

(2D)2-PCANet采用(2D)2-PCA计算特征模板，从行和列的角度同时降维的，因此既有行特征模板又有列特征模板，经过多次实验，得出当行特征模板为5×3的矩阵、列特征模板为5×2的矩阵时的识别率较高。(2D)2-PCANet将原始图像的3个颜色通道看作3幅图像，因此每幅图像经过第一层的特征提取后有18个输出。类似第一层计算特征模板的方法，可以计算出(2D)2-PCANet第二层的2个特征模板，经过多次实验，得出当行特征模板为7×3的矩阵、列特征模板为7×1的矩阵时的识别率较高，由于将第一层的每3个输出组合作为第二层的1个输入，因此每幅图像经过第二层的特征提取后有9个输出。

图2为(2D)2-PCANet深度卷积网络模型，每一层只列出了部分输出。原始的种子图像经过第一层的特征提取后，会得到18个输出，图中只列出了第一层的3个输出，第一层的每3个输出组合在一起作为第二层的1个输入，因此每幅图像在第二层会产生6组输入，每组输入经过第二层的特征提取会产生9个输出，图中只列出第二层的1个输入和其3个输出。然后将第二层的1个输入产生的9个输出二值化并转换成1个十进制矩阵。最后计算直方图，得到该图像的一个表示向量，将其输入到分类器中进行分类。可以看出，相比一层网络，两层网络可以提取图像更多的特征，可以更好地表示图像，因此深度网络可以提高图像的识别率。

图2 (2D)2-PCANet深度卷积网络模型

图3分别为存在0%、5%、10%、15%、20%缺损的种子图像，存在0%缺损的测试集是由所有训练网络的训练集和测试集中的种子图像构成的，共9 189幅图像。表2为两种网络对不同缺损程度的杂草种子图像的识别效果，由识别结果可知，相比PCANet，(2D)2-PCANet对存在缺损的种子图像的识别率会更好一些，对于存在20%缺损的种子图像，(2D)2-PCANet的识别率为74.05%，而PCANet的识别率为71.78%。

(a)0% (b)5% (c)10% (d)15% (e)20%

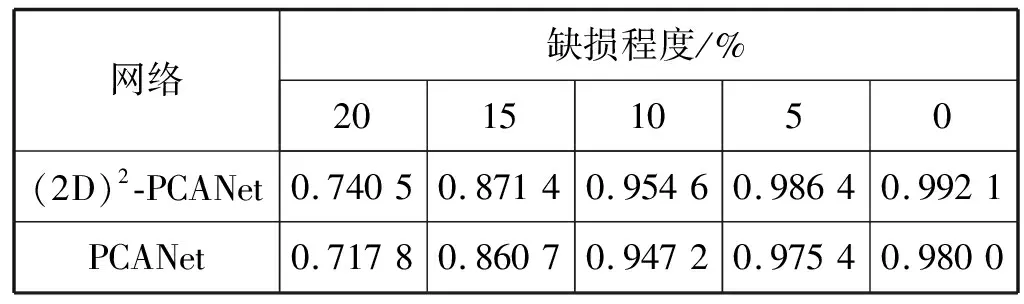
表2 两种网络对缺损图像的识别率

图4分别为存在0°、30°、60°、90°旋转的种子图像，表3为两种网络对不同旋转程度的杂草种子图像的识别效果。对于存在旋转的种子图像，在识别时首先采用PCA方法对图像进行旋转，如图5所示，先通过增加背景的方式使长和宽相等，然后采用PCA方法计算主向量，计算旋转角度，使得图像不再有大幅度的旋转，将旋转后的图像通过切割背景的方式和原图像等长宽，最后再将旋转后的种子图像输入到两个网络。由表3的识别结果可知，相比PCANet，(2D)2-PCANet对存在旋转的种子图像的识别率会更好一些，对于存在90°旋转的种子图像，(2D)2-PCANet的识别率为70.65%，而PCANet的识别率为68.66%，对于存在10°旋转的种子图像，(2D)2-PCANet的识别率为98.38%，而PCANet的识别率为93.06%。

(a)0° (b)30° (c)60° (d)90°

表3 两种网络对存在旋转的图像的识别率

图5 采用PCA旋转图像

图6和图7分别为在y方向和x方向存在偏移的图像。表4和表5分别为两种网络对不同方向偏移的种子图像的识别效果。可以看出，相比PCANet，(2D)2-PCANet对存在缺损的种子图像的识别率会更好一些。对于向右存在10 px偏移的种子图像，(2D)2-PCANet的识别率为73.03%，而PCANet的识别率为63.68%；对于向下存在10 px偏移的种子图像，(2D)2-PCANet的识别率为66.64%，而PCANet的识别率为63.41%。

图6 在y方向存在偏移的图像

图7 在x方向存在偏移的图像

表4 两种网络对在x方向存在偏移的图像的识别率

表5 两种网络对在y方向存在偏移的图像的识别率

为提高图像的识别率，给网络增加了权值训练，表6列出了β为不同值时的识别率，由表可知，当β=0.005时，识别率最高，达到97.84%。

表6 增加权值训练的网络对图像的识别率

尽管采用增加了模板训练的(2D)2-PCANet取得了较好的识别效果，但还是有部分种子会被识别错误，图8列出了部分被识别错误的种子图像，可以看出，有的被错误分类的图像间是非常相似的，这也说明提取的图像的特征区分度不够。

图8 错误识别的种子图像

3 结 语

本文基于(2D)2-PCANet提取杂草种子图像的特征，并采用SVM进行分类，取得97.04%的识别率，相比PCANet的96.44%的识别率要更好一些，增加权值训练的(2D)2-PCANet最高取得97.84%的识别率。采用两种网络分别对存在缺损、旋转和偏移的种子图像进行识别，(2D)2-PCANet的识别率更高。下一步将优化特征模板的初始计算方法，且对于两层以上的网络，可以采用重构到初始输入的方法来训练特征模板。