实现预期轨迹的自动落纱机拔管机构参数优化设计

姜媛媛 张继忠 李永强

摘要：针对平面连杆机构轨迹再现问题，本文以自主设计的自动落纱机拔管机构上料夹的运动轨迹为例，对实现预期轨迹的自动落纱机拔管机构参数进行优化设计。参考人手拔管过程中纱管所处的多个位置，对纱管夹紧装置中料夹的运动轨迹进行路径规划。同时，以机构实际轨迹与预期轨迹距离之差的平方和为目标函数，调用Matlab中的有约束最小化函数fmincon，求解得到双摇杆机构各参数的最优解，并根据得到的最优机构参数，在Adams中建立拔管机构仿真模型进行轨迹仿真。仿真结果表明，经过优化的机构，其实现的轨迹与预期轨迹基本一致，即拔管时，料夹的轨迹与人工拔管的轨迹基本相同，满足拔管机构工作过程中不得与落纱机其他装置干涉的要求，满足预期设计要求。该研究在我国纺织领域具有广阔的应用前景。

关键词：自动落纱机拔管机构; 双摇杆机构; 连杆轨迹; 机构参数优化

中图分类号： TS103.7  文献标识码： A

平面四杆机构因具有结构简单、易加工，方便实现各种复杂运动轨迹等特点，在各类机构设计中被广泛应用[13]。使用平面四杆机构的根本目的在于通过简单的机构形式来实现给定的运动规律或运动轨迹，以完成预定的运动或动作，实现某些复杂的运动要求[4]。落纱机在我国纺织领域广泛应用，随着细纱机运行速度及自动化程度的快速提高，自动落纱装置意义重大。拔管机构为一个双摇杆机构，通过对安装在拔管机构连杆上料夹的运动轨迹进行规划，使拔管机构结构紧凑、工作可靠，并且保证拔管时无干涉或者干涉最小，最终得到拔管机构各参数的最优值。近年来，平面连杆机构轨迹再现问题一直是机构学界研究的热点，许多学者对此进行了大量的研究。王炎等人[5]基于单开链方法，构建具有解耦降次特征的运动学方程组，求解最佳逼近期望轨迹的机构尺寸;王东等人[6]在轨迹已知点的基础上增加了插值节点，使节点分布更加合理;冯立艳等人[7]通过对标准位置基础铰链四杆机构和一般位置带展杆铰链四杆机构的连杆转角傅里叶级数展开研究，完成四杆机构尺度设计，但计算较为复杂;聂雪华等人[8]采用傅里叶描述子提取连杆特征参数，在图谱库确定了满足轨迹要求的连杆机构尺寸;刘传群等人[9]通过虚拟样机与数学分析相结合得到轨迹，再从图谱库中匹配四杆机构，进行优化得到所需连杆机构，工作量较大;杨帆等人[1011]采用改进粒子群算法和修正误差函数法，结合Matlab对四杆机构几何参数进行优化;王琦等人[12]引用改进差分进化算法对平面四杆机构运动轨迹误差进行优化;王良诣等人[13]采用遗传拟牛顿混合算法对四杆机构变量参数进行优化;贺兵等人[14]研究了平面上四杆机构运动轨迹仿真问题，在Matlab/Simulink中进行验证，优化计算原动件的运动规律;李志刚等人[15]采用Pro/E建立曲柄摇杆机构参数化模型，构建优化设计平台，进而得到使其运动轨迹误差最小的设计结果。已有方法均已知关键轨迹点处对应构件的输入角，而对未知关键轨迹点处对应输入角的设计未有涉及。因此，本文以自主设计的自动落纱机拔管机构[16]为例，对其轨迹再现问题进行研究。选用AutoCAD和优化法[1718]相结合的方法，对拔管机构的参数进行优化设计。该设计对我国自动落纱装置的研究具有重要意义。

1 落纱机拔管机构简图建立

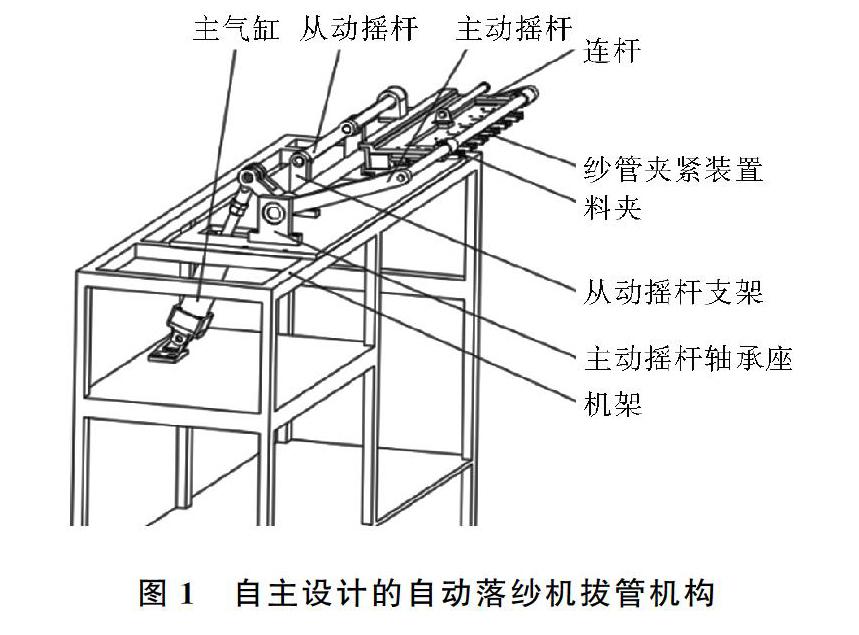
自主设计的自动落纱机拔管机构如图1所示。主气缸动作带动主动摇杆摆动，从而使安装在连杆上的纱管夹紧装置进行运动，实现纱管夹紧装置夹紧纱管、拔管等一系列动作。拔管机构为双摇杆机构，拔管机构运动简图如图2所示。

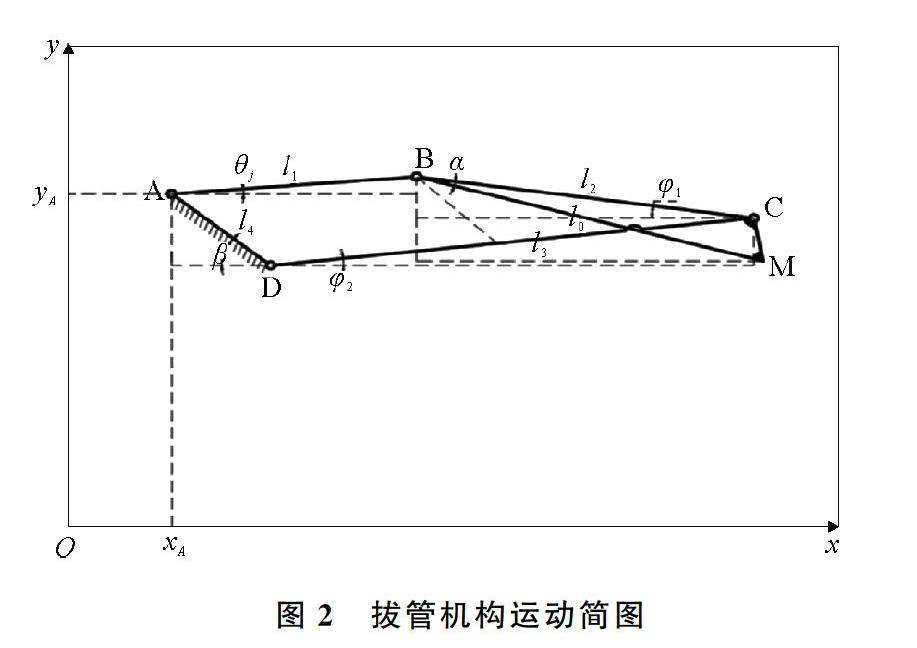
图2中，AD为机架，CD为主动摇杆，AB为从动摇杆，BC为连杆，纱管夹紧装置安装在连杆上，M为连杆展杆上的一点，对应图1中纱管夹紧装置的料夹夹持纱管时接触部分的中点。AB的长度为l1，BC的长度为l2，CD的长度为l3，AD的长度为l4，BM的长度为l0。BM与BC的夹角为α，机架AD与水平位置夹角为β。摇杆AB与水平位置夹角为θj，连杆BC与水平位置夹角为φ1，摇杆CD与水平位置夹角为φ2。A点坐标为（xA，yA）。

2 拔管机构运动过程与预期轨迹确定

自动落纱机拔管机构是自动落纱机的重要组成部分，其作用是将满纱的纱管从锭子上取下。参考人手拔管的轨迹，可以保证在拔下纱管的过程中不对纱管和锭子产生破坏，同时避免纱管在拔管过程中与细纱机其他部件发生干涉。拔管机构拔管的轨迹将决定是否能准确、稳定、安全的将纱管取下。因此，设计满足最佳拔管轨迹的拔管机构具有重要意义。

在自动落纱机运行过程中（如图1所示），當满纱管需要取下时，自动拔管装置开始启动。主气缸动作，带动主动摇杆向下运动到水平位置，同时可以带动安装在连杆上的夹紧装置向下运动到纱管位置，在推进气缸和夹紧气缸的作用下，纱管夹紧装置上的料夹将纱管夹紧。夹紧纱管后，主气缸动作，主动摇杆向上抬起，使纱管和锭子脱离，纱管按照预定的轨迹离开锭子。料夹释放纱管后，拔管装置将进行下一次的拔管过程。

参考人手拔管过程中纱管所处的多个位置，对安装在拔管机构上料夹的运动轨迹进行路径规划，使其与落纱机其他部件不干涉，进而确定出连杆的11个工作位置，应用AutoCAD二维绘图软件，得到M点的轨迹点。部分拔管位置图如图3所示。

应用上述方法设计预期轨迹时，无法得到精确的M点轨迹，仅得到11个关键点位置。利用Matlab中的Spline函数对11个点进行三次样条插值，对轨迹点进行拟合和一定的修正后，得到11个满足要求的关键轨迹点。预期运动轨迹上11个关键点坐标值如表1所示。

3 拔管机构运动轨迹数学模型

3.1 设计变量

在优化设计过程中，设计变量须为独立变量，设计变量的选取对优化设计结果有重要影响。四杆机构的基础尺寸（如图2所示）l1、l2、l3、l4一定时，l0和α的值决定了连杆曲线的形状和大小，xA、yA和β的值决定了连杆曲线的所在位置和方向，θj的初始值决定了连杆曲线的初始位置[19]。连杆轨迹曲线可以用M点坐标表示。平面四杆机构的连杆BC上的M点，在坐标系xoy中的位置决定于l0、l1、l2、l3、l4、α、β、xA、yA九个机构几何参数及连杆AB的转角θj。设计要求M点能最佳地逼近预期轨迹上更多的点，则需要确定以上参数，即设计变量最多有9+j个。由于选轨迹点的方法限制，在关键轨迹点处AB转角均未知，即未给定θj，故将θj作为设计变量。结合AutoCAD，给定预期轨迹上的11个轨迹点。选取设计变量为

X=（l0，l1，l2，l3，l4，α，β，xA，yA，θj）

其中，j=1～11。对于双摇杆机构（如图2所示），将各杆在两轴上分解，得

l1cos θj+l2cos φ1=l3 cosφ2+l4cos β-l1sin  θj+l2sin  φ1=-l3sin  φ2+l4sin  β（1）

消去φ1，则式（1）变换成一个关于φ2的式子，即

k1cos φ2+k2sin  φ2+k3=0（2）

其中

k1=l4cos β-l1cos θj， k2=-l4sin  β-l1sin  θj， k3=k21+k22+l23-l222l3

由式（2）得

φ2=2arctank2+N k21+k22-k23k1-k3（3）

式中，N为位置模式系数，N=±1。若k21+k22-k23<0，则式（3）无解，即按照所求出的杆长无法装配出双摇杆机构。当方程（3）存在解时，φ2有两种可能解，对应有两种机构的装配模式＼[20＼]。在右手直角坐标系中，当B、D、C三点的顺序为逆时针方向时，N=1;反之，N=-1。xoy为右手直角坐标系（如图2所示），结合实际落纱机拔管机构，B、D、C三点顺序为逆时针方向，故应将N=1代入式（3）中进行计算。

结合式（1）和式（3），得

φ1=arctan-l3sin φ2-k2l3cos φ2+k1（4）

用以上参数表达M点的坐标，即

xM=xA+l1cos θj+l0cos α+φ1yM=yA+l1sin θj-l0sin  α+φ1（5）

3.2 目标函数

为使M点能最佳地逼近预期轨迹上更多的点，把机构轨迹与预期要求实现的轨迹距离之差的平方和作为目标函数。通过极小化目标函数得到最优解。其目标函数为

minfx=∑nj=1xj-xjM2+yj-yjM2

式中，xj和yj为第j个综合轨迹点的坐标值;xjM和yjM为第j个预期轨迹点的坐标值。

3.3 约束条件

根据拔管机构所需受力情况，为了保证机构具有良好的传力性能，选择传动角许用值γ=30°。设计时，传动角的最小值大于或者等于许用值。根据要求，列出传动角应满足的条件为

30°-arccosl22+l23-l4-l122l2l3≤0， arccosl22+l23-l4+l122l2l3-150°≤0

4 优化方法和计算结果

连杆机构参数设计问题为多变量有约束非线性函数最优化极小值问题。科学与工程计算软件Matlab提供了多个用于求解最优化问题的函数，其中fmincon函数用于求解多变量有约束非线性函数最小化问题。充分利用Matlab软件在优化设计和矩阵运算方面的优势，通过确立合适的设计变量、建立目标函数和约束条件，利用fmincon函数，求解连杆机构各参数的最优解。

调用Matlab中的fmincon函数，调用格式为

x=fmincon（fun，x0，A，b，Aeq，beq，lb，ub，nonlcon，options）

其中，fun为调用目标函数的函数名;x0为设计变量的初始值，初始值也需在约束范围内;A、b为不等式线性约束的系数矩阵和常数向量，Aeq、beq为等式线性约束的系数矩阵和常数向量，即约束条件为Ax≤b和Aeqx=beq，若没有不等式约束或等式约束，则令A=0，b=0或Aeq=0，beq=0，即在Matlab中输入A=[]，b=[]或Aeq=[]，beq=[];lb和ub为设计变量x的下界向量和上界向量;nonlcon为非线性约束函数的函数名，nonlcon中参数计算非线性不等式约束c（x）≤0和非线性等式约束ceq（x）=0;options表示指定优化参数选项，即用optisons中指定的参数进行最小化设计;求解后得到满足fun函数值最小时的最优解x。

将目标函数、初始值、约束条件、预期轨迹关键点、设计变量上下限等输入，最终得出一组最优解。9个机构几何参数值如表2所示。关键轨迹点处AB转角θj值如表3所示。

5 数据验证

根据优化计算得到的机构几何参数值，修改落纱机拔管机构各零件的尺寸并装配，优化后拔管机构装配简图如图4所示。

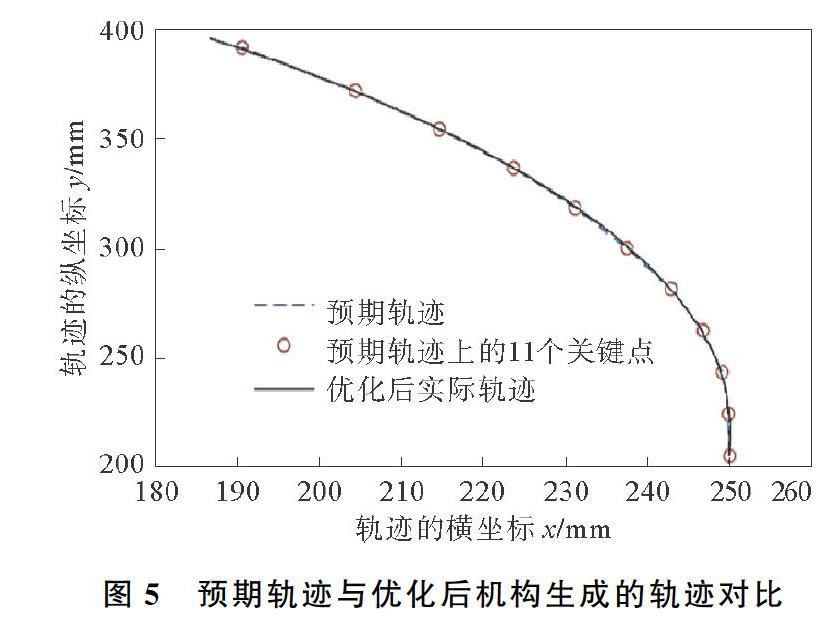
在Adams中建立模型，模拟落纱机的拔管动作，可以得到机构参数优化后的轨迹。将得到的轨迹在Matlab中与原始轨迹进行对比，预期轨迹与优化后机构生成的軌迹对比如图5所示。由图5可以看出，经过优化机构实现的轨迹与本研究预期的轨迹形状基本一致，即拔管时，料夹的轨迹与人工拔管的轨迹基本相同，同时满足了拔管机构工作过程中不得与落纱机其他装置干涉的要求。

6 结束语

自动落纱机的拔管机构是自动落纱机中决定整个机器效率和落纱质量的重要部分。本设计通过采用AutoCAD和建模相结合的方法，得到预期轨迹，再利用Matlab进行优化处理得到最优解，最后将最优解处理后带回模型中，所得轨迹满足设计要求。在传统设计方法中无法得出实际机构精确轨迹的前提下，本文将AutoCAD与数学分析相结合，为预期轨迹的选取提供了一种可行的方法。该方法提高了设计效率，同时也降低了机构设计的盲目性。

参考文献：

[1] 李思聪， 唐正宁. 小剂量灌装机理瓶机构优化设计[J]. 轻工机械， 2020， 38（3）： 1518， 23.

[2] 国春艳. 平面连杆机构优化设计及运动仿真[J]. 内燃机与配件， 2019（13）： 6667.

[3] 呂鲲， 闫明辉. 玻璃上料翻转机构的优化设计[J]. 机械设计与制造， 2015（1）： 157160.

[4] 徐力， 郑传平， 陈翠荣. 五连杆底门机构运动仿真及优化设计[J]. 铁道车辆， 2019， 57（5）： 2123， 5.

[5] 王炎， 杭鲁滨， 刘哲， 等. 电动开启汽车门锁的传动机构连杆轨迹研究[J]. 机械传动， 2019， 43（5）： 5256.

[6] 王东， 陶跃珍. 基于MATLAB三次样条插值的连杆机构轨迹再现优化设计[J]. 机械传动， 2011， 35（1）： 3841.

[7] 冯立艳， 关铁成， 李学刚， 等. 实现期望轨迹的平面铰链四杆机构优化综合[J]. 机械科学与技术， 2018， 37（6）： 848853.

[8] 聂雪华， 王枫红. 采用傅里叶描述子提取连杆曲线特征参数的方法研究[J]. 机械传动， 2015， 39（6）： 4953.

[9] 刘传群， 何勇， 彭达， 等. 转杯纺落纱机械手连杆机构设计[J]. 毛纺科技， 2018， 46（4）： 4650.

[10] 杨帆， 周丽红. 基于运动轨迹误差最小化的平面四杆机构参数优化研究[J]. 组合机床与自动化加工技术， 2019（1）： 7578.

[11] 杨帆. 轨迹生成四杆机构优化及仿真研究[J]. 组合机床与自动化加工技术， 2016（10）： 3539.

[12] 王琦， 何仁. 平面四杆机构运动轨迹多目标综合优化及误差仿真研究[J]. 组合机床与自动化加工技术， 2017（9）： 5558.

[13] 王良诣， 姜礼杰， 王勇. 基于遗传拟牛顿混合算法的四杆机构优化[J]. 合肥工业大学学报： 自然科学版， 2018， 41（2）： 150153.

[14] 贺兵， 吴吉平， 符浩， 等. 基于变速原动件的四杆机构轨迹和速度双目标优化综合[J]. 机械传动， 2016， 40（3）： 7881.

[15] 李志刚， 贾慧芳， 张文亮， 等. 给定运动轨迹的连杆机构新型设计方法[J]. 机械设计与制造， 2013（11）： 4749.

[16] 张继忠， 刘曙光， 张钊. 一种落纱机自动拔管装置： 中国， 201210451312. 5[P]. 20141105.

[17] 孟卫校， 包松东， 魏二涛. 小台面冲压机械多连杆机构的优化设计[J]. 机械工程师， 2020（5）： 4143.

[18] 潘志国， 李心志， 杨然兵， 等. 基于轨迹法的山药播种机送种机构优化设计[J]. 中国农机化学报， 2019， 40（12）： 3033， 40.

[19] Chanekar P V， Ghosal A. Optimal synthesis of adjustable planar fourbar crankrocker type mechanisms for approximate multipath generation[J]. Mechanism and Machine Theory， 2013， 69： 263227.

[20] 黄帆. 曲柄摇杆机构的运动分析研究[J]. 科技视界， 2016（1）： 201， 240.

Parameter Optimization Design of the Drawing Mechanism of Automatic Doffer with Expected Trajectory

JIANG Yuanyuan， ZHANG Jizhong， LI Yongqiang

（School of Electromechanic Engineering， Qingdao University， Qingdao 266071， China）

Abstract：  Aiming at the track reproduction problem of planar connecting rod mechanism， this paper takes the motion track of feeding clip of automatic doffing machine drawing mechanism designed by ourselves as an example to optimize the parameters of automatic doffing machine drawing mechanism to realize the expected track. Referring to the position of the yarn tube in the process of manual tube drawing， the path planning of the material clip in the tube clamping device is carried out. At the same time， taking the square sum of the distance between the actual track and the expected track of the mechanism as the objective function， the constrained minimization function fmincon in Matlab is called to obtain the optimal solution of each parameter of the dual rocker mechanism， and according to the obtained optimal mechanism parameters， a simulation model of the tube drawing mechanism is established in Adams for trajectory simulation. The simulation results show that the trajectory of the optimized mechanism is basically consistent with the expected trajectory， that is， the trajectory of the material clip is basically the same as that of the manual tube drawing， which satisfies the requirement that the mechanism should not interfere with other devices of the doffer during the working process and meet the expected design requirements. This research has a broad application prospect in China's textile field.

Key words： the drawing mechanism of automatic doffer; double rocker mechanism; connecting rod trajectory; mechanism parameter optimization