入口压力与转套式配流系统空化特性关系研究

杜善霄 张洪信 赵清海 姜晓天

摘要：针对转套式配流系统的容积效率下降所产生的振动和噪声，本文主要对凸轮槽型线及入口压力与转套式配流系统空化特性之间的关系进行研究。提出了4种凸轮槽型线，建立了配流系统的Singhal空化模型，并在YST380W型液压综合实验台上进行空化特性仿真实验。仿真结果表明，线性型线空化现象最弱，增大入口压力，线性型线的空化强度最低，样条型线下降趋势最明显;空化占比随入口压力的增大而减小，线性型线的空化占比最低，配流口处样条型线空化占比降低趋势明显，泵腔中样条型线和反正弦型线凸轮槽下降幅度较大;容积效率均随入口压力升高单调递增，线性型线的容积效率最高，且始终保持在92%以上。实验容积效率变化趋势与仿真模拟时基本一致，由于加工误差及转套与油壁之间强剪切作用等因素，实验数据略低于仿真模拟，最大误差为32%，在允许范围内。该研究为转套式配流系统的进一步优化设计提供了理论基础。

关键词：转套式配流系统; 凸轮槽型线; 空化特性; 入口压力; 实验验证

中图分类号： TH137.51  文献标识码： A

转套式配流系统利用柱塞的往复直线运动带动轉套单向转动实现配流，具有体积小、成本低、结构紧凑、配流无滞后等优点，克服了阀式配流系统的诸多弊端[12]。但该系统在进油初始阶段会出现压力的负超调，空气或者蒸汽从油液中分离出来，出现两项共存的状态，即空化[35]。空化现象会显著降低系统的工作性能及容积效率，引起系统强烈的振动和噪声，严重影响系统的正常工作[6]。近年来，一些研究人员对转套式配流系统进行研究，徐威等人[7]建立了3种不同凸轮槽型线转套的运动学模型，分析了不同凸轮槽型线对转套式配流系统运动学特性的影响，但未研究凸轮槽型线对转套式配流系统空化的影响;张延君等人[8]初步引入了空化模型，分析了空化对系统的影响，此研究是在特定凸轮槽型线和恒定入口压力下进行，并未深入分析不同凸轮槽型线及入口压力对空化的影响，且研究过程以水为流体介质，也并未考虑转套与泵体之间径向间隙的存在。基于此，本文主要对凸轮槽型线及入口压力与转套式配流系统空化特性之间的关系进行研究，重新设计4种新的凸轮槽型线，基于含有转套间隙的流体域仿真模型，以油液为工作介质，深入分析凸轮槽型线及入口压力与转套式配流系统空化特性之间的关系，并在YST380W型液压综合实验台上进行仿真实验。研究结果表明，转套式配流系统在工作时，可通过增大入口压力降低空化的影响。

1 转套式配流系统空化模型

转套式配流系统以柱塞的直线运动带动转套单向转动，通过转套上的配流口分别与进、出油腔连接，以实现配流功能[912]。转套式配流系统工作原理如图1所示，转套式配流系统流体域模型如图2所示。

转套式配流系统的流体域随柱塞和转套的运动进行周期性变化，配流口跟随转套同步运动。柱塞上行时，系统在进流质阶段，泵腔容积逐渐增大;柱塞下行时，系统在排流质阶段，泵腔容积逐渐减小。系统工作时，柱塞轴向位移与曲轴转角之间的关系为

z=r01-cos φ+λ2sin2φ（1）

式中，z为柱塞轴向位移，m;φ为曲轴转角，φ=ωt;t为时间，s;ω为曲轴角速度，rad/s，ω=2πn/60;n为曲轴转速，r/min;λ为曲柄连杆比，其中λ=r0/l0，r0为曲轴半径，m;l0为连杆长度，m。

为保证转套随柱塞的往复运动而单向转动，对凸轮槽径向深度进行设计，径向方程控制凸轮槽深度变化并在上下止点处实现阶跃，其与转套转角之间的关系为

r（θ）=d2+h2-3Δhθ2π2+2Δhθ3π3， 0≤θ<πd2+h2-3Δhθ-π2π2+2Δhθ-π3π3，  π≤θ<2π （2）

式中，r为凸轮槽径向深度，m;d为柱塞直径，m;Δh=h2-h1为凸轮槽深度变化，m;h1为凸轮槽最小深度，m;h2为凸轮槽最大深度，m;θ为转套的转角，rad。

设计4种转套式配流系统凸轮槽型线结构。反正弦凸轮槽型线转套转角与曲轴转角之间的关系为

θ1=-π2cosπzS+π2， 0≤φ<π π2cosπzS+3π2， π≤φ≤2π （3）

式中，z为式（1）柱塞轴向位移关于曲轴转角φ的函数。

线性凸轮槽型线转套转角与曲轴转角之间的关系为

θ2=πzS， 0≤φ<π2π-πzS， π≤φ≤2π （4）

式中，z为式（1）柱塞轴向位移关于曲轴转角φ的函数。

正切凸轮槽型线转套转角与曲轴转角之间的关系为

θ3=32arctan23zS-3+π2， 0<φ≤π32arctan3-23zS+3π2， π<φ≤2π （5）

式中，z为式（1）柱塞轴向位移关于曲轴转角φ的函数。

样条凸轮槽转套转角与曲轴转角之间的关系为

θ4=3πz2/2S2，0<φ≤（17π/30）π1-31-zS2，1730π<φ≤ππ1+31-zS2，π<φ≤4330π2π-（3πz2/2S2），（43π/30）<φ≤2π （6）

式中，z为式（1）柱塞轴向位移关于曲轴转角φ的函数。

由于Singhal空化模型考虑空化影响因素更加全面，因此选取Singhal空化模型对转套式配流系统进行空化仿真[1316]。忽略二阶项、液体黏度及表面张力对球泡生长的影响，空泡动力学基本方程可简化为

dRdt==23pb-pcρ（7）

其中，R为球泡表面半径;pb为泡表面压力;pc为局部远场压力。

气液传质的蒸发率和冷凝率分别为

se=Cekσρlρv1-fv-fg23p′v-pρl（8）

sc=Cckσρlρlfv23p-p′vρl（9）

式中，ρv为气相密度;ρv=0476 9 kg·m-3;ρl为液相密度，ρl=865 kg·m-3;fg为永久性气体质量分数，fg=40 mg/L;fv为蒸汽质量分数，fv=0;p为液体压力;pv为饱和蒸气压，pv=400 Pa;σ为液体表面张力系数，σ=003 N·m-1;推荐经验系数值Ce=002，Cc=001。

仿真计算时利用Fluent软件中的自定义函数（user define function，UDF）功能，确保流体域运动的进行，采用kε湍流模型、SIMPLE压力速度耦合算法及一阶迎风格式离散化处理方法进行迭代计算，进一步讨论入口压力对空化的影响[1720]。

2 凸轮槽型线与空化的关系

2.1 标定工况下空化特性分析

轉套式配流系统空化现象产生于进油初始阶段，空化气体主要集中在配流口和泵腔中。分别对4种凸轮槽型线在标定工况下（转速为500 r/min，入口压力为01 MPa，负载压力为10 MPa）进行空化仿真研究，不同凸轮槽型线气体分布如图3所示。

由图3可以看出，样条型线空化现象最强，当工作时间为0015 s时，气体体积分数最高为2818%，整个空化过程持续时间占据单个工作周期的1933%;反正弦型线和正切型线空化现象依次减弱，线性型线空化现象最弱，当工作时间为0008 s时，配流口内气体体积分数最大仅为802%，而整个空化过程占据单个工作周期的1233%;泵腔内各凸轮槽型线气体体积分数变化趋势与配流口中一致，但同一型线下整体空化作用明显高于配流口，样条型线最大气体体积分数为4615%，空化时间占据单个工作周期的23%;而空化作用最小的线性型线最大气体体积分数达到2716%，空化时间占单个工作周期的16%。标定工况下，线性型线在工作过程中整体空化作用最低、持续时间最短，明显优于其余3种型线。

2.2 不同入口压力下空化特性分析

入口压力的变化会影响转套式配流系统的空化特性。针对本设计选用的4种凸轮槽型线，设定转速为500 r/min，负载压力为10 MPa，在不同入口压力下进行空化性能仿真研究，用以确定配流系统最佳工作压力区间，为实验研究提供了理论基础。

用最大气体体积分数表示空化强度，最大气体体积分数为

α=VpmaxV×100%（10）

式中，Vpmax为最大瞬时气体体积，m3;V为系统总体积，m3。

α越大，空化的强度越大，系统受到的冲击也就越大。在不同凸轮槽型线配流口和泵腔内部，最大气体体积分数与入口压力间的关系如图4所示。由图4可以看出，泵腔中的空化强度高于配流口，配流口和泵腔中的最大气体体积分数均随入口压力的升高而下降，样条型线总体下降趋势最大，配流口处当入口压力低于03 MPa时，样条型线最大气体体积分数最高，入口压力高于03 MPa后，最大气体体积分数样条型线低于反正弦型线，但仍然高于正切型线;泵腔中当入口压力高于05 MPa时，样条型线最大气体体积分数低于反正弦型线和正切型线。线性型线的最大气体体积分数最低，随着入口压力的增大，在配流口中趋于5%以下，泵腔中趋于15%以下。

为了更全面的分析空化特性，引入空化占比的概念，空化占比为

τ=tcT×100%（11）

式中，tc为单个工作周期内空化持续时间，s;T为工作周期，s。τ越大，空化现象持续的时间就越长。

在配流口和泵腔内部，不同凸轮槽型线空化占比与入口压力的关系如图5所示。由图5可以看出，随着入口压力的升高配流口和泵腔内各型线空化占比均呈减小趋势，泵腔中空化占比高于配流口，四种凸轮槽型线中，线性型线的空化占比最低，空化持续时间最短;配流口处样条型线空化占比降低趋势明显，当入口压力

高于04 MPa时，最大气体体积分数低于反正弦型线，但仍高于正切型线;泵腔中样条型线和反正切型线凸轮槽空化占比下降幅度较大，而正切型线下降趋势较为平缓，当入口压力高于04 MPa时，正切型线空化占比最高。

容积效率是衡量转套式配流系统工作状况的重要指标，空化产生的气体会阻碍流质进入，降低容积效率。容积效率为

ηv=QcQt×100%（12）

式中，Qc和Qt分别为实际输出流量和理论输出流量，m3/min。

在不同入口压力下，不同凸轮槽型线的容积效率与入口压力关系如图6所示。4种凸轮槽型线的容积效率均随入口压力升高单调递增，反正弦型线、正切型线和样条型线在入口压力小于07 MPa时增大趋势明显，随着入口压力的继续升高容积效率稳步提升，当入口压力高于05 MPa时，3种凸轮槽型线配流系统容积效率均在90%以上，可见适当提高入口压力可显著提升容积效率;线性型线的容积效率增加较平缓，但相同入口压力下容积效率最高，且始终保持在92%以上较高水平，具有良好的稳定性。总之，线性型线的容积效率最高，样条型线的提高幅度最大。

3 空化特性实验研究

实验只对空化特性最优的线性型线，验证理论模型的准确性。在YST380W型液压综合实验台上进行实验。转套式配流系统的整体结构依据液压综合实验台进行设计，并装配到实验台上。液压综合实验台可

对系统的容积效率进行监测，容积效率可直接从控制系统上电脑显示区域读取。

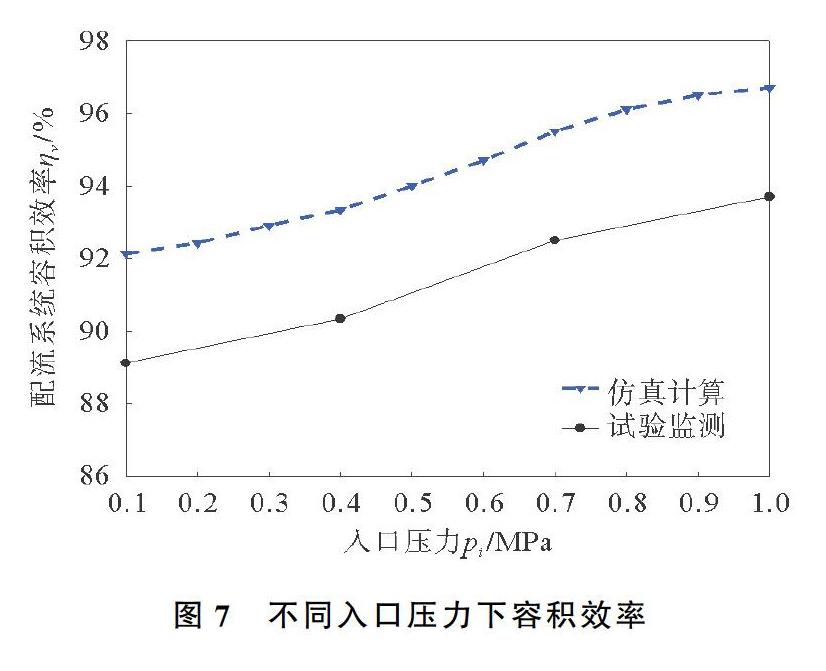
实验工况设定与仿真模拟时一致，设定工作转速500 r/min，出口压力设定为10 MPa。受供油压力调节旋钮精度限制，实验增大压力间隔，逐步增大入口压力。在不同入口压力条件下，监测到配流系统容积效率变化与仿真模拟对比，不同入口压力下容积效率如图7所示。由图7可以看出，实验容积效率变化趋势与仿真模拟时基本一致，由于加工误差以及转套与油壁之间强剪切作用等因素，实验数据略低于仿真模拟，最大误差为32%，在允许范围内。

4 结束语

本文主要研究了转套式配流系统的空化模型，通过对系统容积效率实验，计算仿真最大误差为32%。同时，对4种凸轮槽型线的气体体积分数分析发现，样条型线空化现象最强，反正弦型线和正切型线空化现象依次减弱，线性型线空化现象最弱，增大入口压力，线性型线的空化强度最低，样条型线下降趋势最明显。4种凸轮槽型线的空化占比随入口压力的增大而减小，线性型线的空化占比最低。4种凸轮槽型线的容积效率均随入口压力升高单调递增，当入口压力高于05 MPa时，反正弦型线、正切型线和样条型线容积效率均在90%以上，线性型线的容积效率最高，且始终保持在92%以上。由此可见，线性型线的空化特性最优，且转套式配流系统在工作时，可通过增大入口压力降低空化的影响。该研究为转套式配流系统进一步优化设计提供了理论依据。

参考文献：

[1] 张洪信， 程联军， 张铁柱， 等. 往复柱塞泵转套式配流系统的结构原理[J]. 流体机械， 2015， 43（8）： 4851.

[2] 徐威. 往复柱塞泵转套式配流系统性能仿真与结构优化研究[D]. 青岛： 青岛大学， 2016.

[3] 盛敬超. 液压流体力学[M]. 北京： 机械工业出版社， 1980.

[4] Wylie E M， Streeter V L. Fluid transients[M]. Ann Arbor： Michigan University Press， 1978.

[5] 张也影. 流体力学[M]. 北京： 高等教育出版社， 2004.

[6] 潘中永， 袁寿其. 泵空化基础[M]. 镇江： 江苏大学出版社， 2013.

[7] 徐威， 张洪信， 张铁柱， 等. 转套式配流系统凸轮槽型线及其运动学特性研究[J]. 机械強度， 2017， 39（4）： 882886.

[8] 张延君， 张洪信， 赵清海， 等. 转套式配流系统内部流场空化现象研究与分析[J]. 青岛大学学报： 工程技术版， 2017， 32（4）： 7275.

[9] 青岛大学. 一种往复柱塞泵用转套式周向配流装置： 中国， CN201310706745. 5[P]. 20140312.

[10] 姜晓天， 张洪信， 赵清海， 等. 转套式配流系统U型减振槽结构设计优化[J]. 机械科学与技术， 2019， 38（1）： 2329.

[11] 张延君. 转套式配流系统工作性能仿真研究[D]. 青岛： 青岛大学， 2018.

[12] 张延君， 张洪信， 赵清海， 等. 转套式配流系统U型减振槽结构及其对流场影响[J]. 机械制造与自动化， 2019， 48（1）： 1114.

[13] Schnerr G H， Sauer J. Physical and numerical modeling of unsteady cavitation dynamics[C]∥ProceeDings of 4th International Conference on Multiphase Flow. New Orleans， USA： ICMF， 2001.

[14] Singhal A K， Athavale M M， Li H Y， et al. Mathematical basis and validation of the full cavitation model[J]. ASME Trans. J. Fluids Eng， 2002， 124 （3）： 617624.

[15] Zwart P J， Gerber A G， Belamri T. A twophase flow model for predicting cavitation dynamics[C]∥ICMF 2004 International Conference on Multiphase Flow. Yokohama， Japan： ICMF， 2004.

[16] Niedzwiedzka A， Schnerr G H， Sobieski W， et al. Review of numerical models of cavitating flows with the use of the homogeneous approach[J]. Archives of Thermodynamics， 2016， 37（2）： 7188.

[17] Smagormsky J. General circulation experiments with the primitive equations [J]. Monthly Weather Review， 1963， 91（3）： 99164.

[18] 施卫东， 李通通， 张德胜， 等. 轴流泵叶轮区域空化特性数值模拟[J]. 农业工程学报， 2012， 28（13）： 8893， 295.

[19] 张延君， 张洪信， 赵清海， 等. 往复柱塞泵转套式配流系统泵腔流场仿真研究[J]. 液压与气动， 2016（11）： 3135.

[20] 阮辉， 廖伟丽， 罗兴锜， 等. 叶片低压边的轴面位置对高水头水泵水轮机空化性能的影响[J]. 农业工程学报， 2016， 32（16）： 7381.

Study on the Relationship Between Inlet Pressure and Cavitation Characteristics of Rotary Sleeve Distribution System

DU Shanxiao， ZHANG Hongxin， ZHAO Qinghai， JIANG Xiaotian

（Power Integration and Energy Storage System Engineering Technology Center of Qingdao University， Qingdao 266071， China）

Abstract：  For the vibration and noise generated by the volumetric efficiency reduction of the rotary sleeve flow distribution system， this paper mainly studies the relationship between the cam groove profile and the inlet pressure and the cavitation characteristics of the rotary sleeve flow distribution system. Four kinds of cam groove profiles are proposed， and the Singhal cavitation model of the flow distribution system is established， and the cavitation characteristic experiment is carried out on the YST380W hydraulic comprehensive experimental platform. The simulation results show that the linear profile cavitation phenomenon is the weakest. When the inlet pressure is increased， the linear profile cavitation intensity is the lowest， and the spline profile has the most obvious downward trend. The proportion of cavitation decreases with the increase of the inlet pressure， the proportion of cavitation of the linear profile is the lowest， the spline profile at the distribution port decreases significantly， and the spline profile and arc tangent profile in the pump cavity have a larger decline. Volumetric efficiency increases monotonically with the increase of inlet pressure， the linear profile is the highest， and it always remains above 92%. The change trend of the experimental volume efficiency is basically the same as that in the simulation. Due to the processing error and the strong shear between the sleeve and the oil wall， the experimental data is slightly lower than that in the simulation. The maximum error is 32%， which is within the allowable range. This research provides a theoretical basis for the further optimization design of the rotary sleeve flow distribution system.

Key words： rotary sleeve distribution system; cam groove line; cavitation; inlet pressure; test verification