含源项的Smoluchowski方程的预李群分类

林府标，张千宏

(贵州财经大学数学与统计学院，贵阳 550025)

Smoluchowski凝聚方程[1-2]

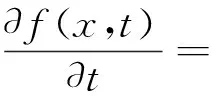
(1)

是既含偏导数又含积分项的非线性积分—偏微分方程，历史悠久，应用领域广泛[1-5].x表示粒子的尺寸或体积或质量，f(x，t)表示种群密度分布函数，t表示时间.K(x，y)是内核聚合函数，表示体积或质量分别是x和y的粒子生成体积或质量为x+y的粒子的合成率，并且具有非负对称性

K(x，y)=K(y，x)≥0.

(2)

鉴于许多实际模型应用的需要，不同类型的众多核函数已被提出[5-7]，例如描述稀气相系统中的碰撞自由分子核函数. 诸多实际应用领域中，核函数在物理和化学中的应用是最广泛的[6]，其它应用领域还涉及生物科学和天文学等. 但是一类既重要又有广泛应用领域的核函数是γ次齐次核函数[7]，即存在某个幂指数γ满足齐次核函数方程

K(σx，σy)=σγK(x，y)，

(3)

对任意的常数σ，x，y>0皆成立. 特别地，三类简单且数学上容易处理的重要γ(γ=0，1，2)次齐次核函数K(x，y)分别为

K(x，y)=k0，k1(x+y)，k2xy，

(4)

其中，k0，k1，k2均为正常数，γ(γ=0，1，2)次齐次核函数(4)在云滴聚合中的应用可参见文献[4]. 另外，利用性质(3)容易证明γ次齐次核函数满足方程

xKx(x，y)+yKy(x，y)=γK(x，y)，

(5)

从而可得到此一阶线性偏微分方程(5)的一般解为

(6)

其中，H是一个任意一元可微函数. 若令变换y=xs，利用齐次核函数的性质(3)或(6)式可以得到

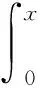
(7)

注意到(7)式，带齐次核函数(3)的方程(1)可以改写并记为

(8)

同时考虑既有聚合又有破损过程的群体平衡方程[5]可以写成

(9)

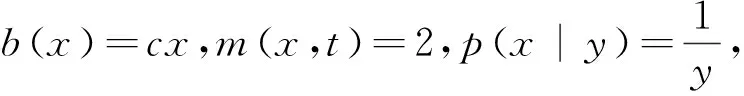
(10)

鉴于群体平衡方程(9)和(10)与方程(8)有着密切的结构特征以及实际应用和理论探究的需要，研究带齐次核函数(3)并具有任意项源函数S(x，t，f)的非齐次Smoluchowski方程

Lf=S(x，t，f)

(11)

的结构、性质、显式解析解等都是具有实际应用价值和理论意义的，其中算子Lf见齐次方程(8)．

虽然方程(1)的应用领域广泛[2-5]，但对任意的核函数(2)一般是很难精确求解的，甚至可以说要找到方程(1)的显式解析解几乎是不可能的. 甚至对极少数的特殊齐次核函数K(x，y)，方程(8)的精确解也是知之甚少的，除非采用数值方法或实验技术，例如文献[8]. 因此一方面，需要不断创新和探索精确求解的一些新方法和技术；另一方面，有时候即便求出了解析解，或是以隐函数形式出现，或不便于实际模型的应用. 例如对常数核函数K(x，y)=k0，1940年Schumann[3]给出了方程(8)的一个隐式解析解

(12)

隐式解析解(12)的柯西问题对应的初始密度分布函数和一阶矩V分别为

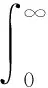
经典李群分析法[9-12]不能直接用于解析求解积分—偏微分方程(8)和(11)，而需要采用改进的李群分析法[13-14]. 近些年来，改进的李群分析法[13-14]在许多学科领域得到了进一步应用和发展，特别地在探究积分—偏微分方程、时滞偏微分方程和随机微分方程的显式解析解和完全群分析方面是一个行之有效的工具[15-25]. 然而利用改进的李群分析法[13-14]求解非齐次积分—偏微分方程(11)的决定方程时却非常困难，甚至几乎是不可能的. 该决定方程的求解依赖于积分—偏微分方程(11)本身的结构性质和特征，而不像用经典李群分析法[9-12]求解偏微分方程的决定方程那样有相对普遍和适用的统一有效解法．

预李群分类法以一种建议性和启发性的思维方法首次呈现在文献[26]中，最初用于偏微分方程，近几年来预李群分类法[26-27]作为研究偏微分方程的部分群分析、群不变解和解析解的工具之一，已得到深入的改进[28]和受到学术界的关注[29]. 随着改进的李群分析法[13-14]在许多非线性科学领域的应用，特别是在积分—偏微分方程中的应用[15-23，25]. 促使预李群分类法[26-28]得到进一步研究和发展，特别是已被用于研究带任意项源函数的非齐次积分—偏微分方程、群体平衡方程和Boltzmann方程[17，30]．

本文在前人的工作和文献[25]的基础上，利用预李群分类法探究带有任意项源函数的非齐次积分—偏微分Smoluchowski方程(11)的部分群分析．

1方程(8)接受的李群和最优化子李代数系统

文献[31-32]借助于覆盖的概念以及将积分—偏微分方程转化为边界和泛函微分方程组，给出了方程(8)的对称. 文献[25]利用改进的李群分析法[13-14]和文献[16-18]求解积分—偏微分方程的决定方程的算法框架也给出了方程(8)的决定方程的通解和所接受的不变群的对称算子

(13)

特别地，带常数核函数K(x，y)=k0的方程(8)所接受的不变群的对称算子为

(14)

带和核函数K(x，y)=k1(x+y)的方程(8)所接受的不变群的对称算子为

(15)

带乘积核函数K(x，y)=k2xy的方程(8)所接受的不变群的对称算子为

(16)

应用构造积分—偏微分方程精确解的方法[13-14]和预李群分类法[17，30]研究方程(8)和(11)的群分析、群不变解和显式解析解，需要构造方程(8)的不变群的全体生成元(13)的三维李代数L3=span{X1，X2，X3}的最优化子李代数系统，其中相应的γ=0，1，2.

根据算法[13-14]和李代数L3=span{X1，X2，X3}的交换运算表1得内自同构

表1 李代数L3=span{X1，X2，X3}的交换运算表

求解对应的李方程得内自同构相应的李群分别为

其中bi(i=1，2，3)分别是对应李群Ai(i=1，2，3)的群参数.根据文献[33]中的两步算法获得三维李代数L3=span{X1，X2，X3}的一维、二维和三维最优化子李代数系统分别为

{X1}，{X2}，{X3}，{X1+(1+γ)X2+εX3}，

{X1+αX2}，{X1+αX2，X3}，{X1，X2}，{X2，X3}，

{X1，X2，X3}，α∈，ε=±1.

2预李群分类法

既然非齐次积分—偏微分方程(11)对应的齐次积分—偏微分方程(8)的对称和全部群分析已给出，这暗示可以充分利用预李群分类法的算法思想[26-28]来探究非齐次积分—偏微分方程(11)的性质、结构、对称、群不变解和显式解析解以及源函数S的群分类等.因此，在偏微分方程的预李群分类法[26-28]和积分—偏微分方程的预李群分类法[17，30]的启发下，探究非齐次积分—偏微分方程(11)的预李群分类算法．

2.1预李群分类算法和方程(11)的决定方程

方程(8)接受的无穷小李对称算子(13)对应的标准Lie-Bäcklund算子[12-14]为

假设方程(11)接受的标准Lie-Bäcklund算子[12-14]为

这里cj(j=1，2，3)是常数，则算子X相应的标准Lie-Bäcklund延拓算子[12-14]变成

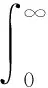
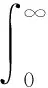
xKx(x，y)f(y，t)]dy.

(17)

(1+γ)tDt(Lf)-xDx(Lf)，

(18)

c2(f+tft)-c3ft]Sf，

[(1+γ)tft-xfx]·

g(s)=[(1+γ)tft(x(1-s)，t)-

x(1-s)fx(x(1-s)，t)]f(xs，t)+

f(x(1-s)，t)[(1+γ)tft(xs，t)-xsfx(xs，t)].

剩余的情形可以类似地通过计算给出. 因此，非齐次积分—偏微分方程(11)的决定方程[12-14]为

(19)

这里|(11)表示方程(11)的任一解f=f(x，t)都满足决定方程(19). 注意到Lf=S和算子(18)，决定方程(19)具体变成

c1xSx+[c3+(c2-c1(1+γ))t]St-

c2fSf=[c1(1+γ)-2c2]S.

(20)

2.2获得决定方程(20)的另外一种方法

鉴于齐次积分—偏微分方程(8)所接受的不变群的无穷小李对称算子(13)较简单且构成的李代数的维数是有限的，决定方程(20)可以利用相应的一维李群变换法而得到. 事实上，方程(11)的任一解被算子(13)对应的李群变换映射为同一方程的解. 因此，构造一个被变换的任一解代入该方程，然后关于群参数求导并取群参数为零即可获得决定方程(20)，其具体算法核心思想阐述如下. 首先求解对称算子(13)对应的李方程得其相应的李群为

其中aj∈(j=1，2，3)是群参数. 假设g=g1∘g2∘g3是李群gj(j=1，2，3)的合成，则得到群g为

(21)

(22)

把李群g和g-1的相应变换和(22)式代入方程(21)，运用齐次核函数的性质(3)或(6)式，通过计算整理可以获得

S(xea1，tea2-(1+γ)a1+a3ea2-(1+γ)a1，fe-a2)=

f(x(1-s)，t)f(xs，t)ds+

(23)

根据假设条件李群g把方程(11)的任一解f=f(x，t)变换成同一方程(21)的解，所以方程(23)变成

S(xea1，tea2-(1+γ)a1+a3ea2-(1+γ)a1，fe-a2)=

e(1+γ)a1-2a2S(x，t，f).

(24)

进一步取ai=cia(i=1，2，3)，其中ci∈(i=1，2，3)和a∈均为群参数. 对方程(24)两边同时关于群参数a求导并令a=0，则可以得到决定方程(20)．

在齐次方程(8)所接受的无穷小李代数的维数有限且较简单的前提下，采用预李群分类法获得非齐次方程(11)的决定方程(20)的后一种方法比前一种更简捷．

3方程(11)的预李群分类

决定方程(19)和(20)具有兼容性，由于当S=0时它们都有相同的解.决定方程[12-14](19)并不需要很困难地按照求解积分—偏微分方程的决定方程[15-23，25]的启发探索性思维去探求通解，相反却是求解一个关于源函数S(x，t，f)的一阶线性非齐次偏微分方程(20). 鉴于预李群分类算法的核心思想，因此采用决定方程(20)探究源函数S(x，t，f)和带齐次核函数(4)的方程(11)的部分群分析．

3.1源函数S(x，t，f)的求解

情形1一维子李代数{X1+αX2}.

X1+αX2:c1=1，c2=α，c3=0.

把系数ci(i=1，2，3)的值分别代入决定方程(20)得

xSx+(α-1-γ)tSt-αfSf=(1+γ-2α)S.

对任意一个连续可微的二元函数ψ，该一阶线性非齐次偏微分方程的一般解可写成

(25)

情形2二维子李代数{X1+αX2，X3}.

X1+αX2:c1=1，c2=α，c3=0，

X3:c1=0，c2=0，c3=1.

把系数ci(i=1，2，3)的两组值分别代入决定方程(20)得

xSx+(α-1-γ)tSt-αfSf=(1+γ-2α)S，

St=0.

对任意一个连续可微的一元函数φ，该一阶线性非齐次偏微分方程组的一般解为

S(x，t，f)=x1+γ-2αφ(xαf)，α∈.

情形3三维子李代数{X1，X2，X3}.

X1:c1=1，c2=0，c3=0，

X2:c1=0，c2=1，c3=0，

X3:c1=0，c2=0，c3=1.

把这些系数ci(i=1，2，3)的值都分别代入决定方程(20)得

xSx-(1+γ)tSt=(1+γ)S，

tSt-fSf=-2S，St=0.

对任一常数c，该一阶线性非齐次偏微分方程组的一般解为

S(x，t，f)=cx1+γe2f.

剩余子李代数对应方程(11)的源函数S(x，t，f)可以类似地求出，为了行文简洁，不再一一给出其求解过程，其相应结果列于表2至表5．

3.2方程(11)的群不变解

情形1K(x，y)=k0，{Y1+αY2}.

(26)

其中，φ(z)满足约化的积分—常微分方程

(27)

(28)

显式解析解(28)满足性质当t→+∞,f(x，t)→0和当x→+∞,f(x，t)→0. 它们分别表明非负显式解析解(28)是渐近稳定的和对任意尺寸(质量或体积)足够大的微粒子其种群密度分布函数必然为零[5]. 显式解析解(28)对应的边界条件和柯西问题的初值条件分别为

用显式解析解(28)易计算出种群的平均总量M0(t)(零阶矩)和种群的总质量M1(t)(一阶矩)在t时刻分别为

(29)

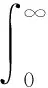
受(29)式中一阶矩M1(t)数值结果的启发，对带一般非负核函数(2)的方程(1)的任一解f(x，t)，性质(29)中的一阶矩仍然为常数，即种群的总质量仍然保持守恒. 事实上，用x乘以方程(1)的两边，然后从0到∞关于x积分，交换二重积分的积分次序后再利用核函数的对称性(2)容易证明

(30)

(30)式表明对带一般非负核函数(2)的方程(1)的任一解f(x，t)满足种群质量守恒，即一阶矩μ1(t)满足恒等式

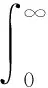
情形2K(x，y)=k1(x+y)，{Z1+αZ2}.

其中，函数φ(z)满足约化积分—常微分方程(39)．

情形3K(x，y)=k2xy，{T1+αT2}.

其中，函数φ(z)满足约化积分—常微分方程(44)．

剩余的子李代数对应的群不变解可以类似求出，其结果列于表2至表4.其中二维和三维子李代数对应方程(11)的群不解，需要研究二维和三维子李代数的一维最优化子李代数分类.由于求解的方法与前面的情形类似，故为了行文简洁，省略其具体求解过程，仅把其相应源函数的分类结果列于表5．

表2 带源函数S(x，t，f)的方程(11)的群不变解和约化方程，K(x，y)=k0，ε=±1Tab.2 The invariant solutions and reduced equations of equation (11) withthe source term S(x，t，f)，where K(x，y)=k0，ε=±1

表3 带源函数S(x，t，f)的方程(11)的群不变解和约化方程，K(x，y)=k1(x+y)，ε=±1Tab.3 The invariant solutions and reduced equation of equation (11) withthe source term S(x，t，f)，where K(x，y)=k1(x+y)，ε=±1

续表2

表4 带源函数S(x，t，f)的方程(11)的群不变解和约化方程，K(x，y)=k2xy，ε=±1Tab.4 The invariant solutions and reduced equation of equation (11) withthe source term S(x，t，f)，where K(x，y)=k2xy，ε=±1

表5 带齐次核函数(3)的方程(11)的源函数S(x，t，f)的群分类Tab.5 The group classfication of the source function S(x，t，f) for equation (11) with the homogeneous kernel (3)

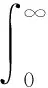
(31)

(32)

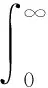
(33)

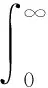
(34)

ε=±1，

(35)

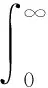
ψ(x，φ)=0，

(36)

(37)

ε=±1，

(38)

(39)

(40)

(41)

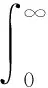
(42)

εzφ′+3εφ+

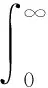
(43)

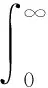
(44)

4结论与探讨

利用预李群分类法给出了非齐次积分—偏微分方程(11)的决定方程的两种算法. 应用预李群分类法获得了带源函数的非齐次积分—偏微分方程(11)的部分群分析、源函数的解析式、群不变解、显式解析解和约化的积分—常微分方程. 所获得结果表明预李群分类法不但能应用于带源函数的积分—偏微分方程而且是行之有效的解析求解工具之一．

采用改进的李群分析法[13-14]直接研究非齐次积分—偏微分方程(11)的完全李群分析，是一个棘手的问题，包括对任意项源函数S(x，t，f)的李群分析. 另外，如何运用改进的李群分析法[13-14]探究积分—偏微分方程(9)和带非齐次核函数(2)的积分—偏微分方程(1)的对称、群不变解、约化的积分—常微分方程和显式解析解等都值得在今后的研究工作中进一步深思和探讨．