非均质岩层引起的偏压对盾构隧道受力影响分析

伍鹏李 王春凯 齐明山

摘 要：西南、西北以及东南等地区地质复杂，对地铁盾构隧道结构有较大影响。文章以贵阳市轨道交通 3 号线为工程背景，采用二维数值模型，对非均质岩层引起偏压受力下的盾构隧道管片受力进行分析，分析结果初步得出分层面上下岩层弹性模量之比、分层面倾角和位置对盾构隧道管片受力的影响规律，以期为相似地质条件下地铁建设提供依据。

关键词：地铁;非均质岩层;盾构隧道;受力特性

中图分类号：U451

随着隧道与地下工程在我国铁路、公路等交通运输领域中的不断发展，西南、西北以及东南地区不同等级铁路、公路和地铁等隧道设计施工面临的地质愈加复杂，顺层和非均质地层的隧道偏压问题逐渐增多，且会极大影响隧道施工安全与隧道稳定性[1-5]。软硬岩相交的地层是山岭隧道修建过程中常遇到的地质情况，当隧道穿越硬岩与含煤地层交界且岩层产状平行于隧道轴线时，由于岩层分界面两侧的围岩物理力学性质差异较大，例如，一侧围岩自稳能力较弱，另一侧自稳能力较强[6]，在衬砌形成之后，作用在衬砌结构上的荷载不对称，引起结构的内力和变形也不对称，这种不对称的偏压程度往往与层面倾角大小和层面位置有直接关系。周晓军[7]通过理论分析和模型试验2种方法对地质顺层偏压隧道围岩作用在衬砌结构上的荷载进行了研究分析，提出了顺层偏压隧道围岩压力计算方法。邓彬[8]采用理论分析与有限元数值计算相结合的方法，研究了地质顺层岩体中单线铁路隧道偏压作用的计算方法，并分析了倾角、岩层厚度等影响。王磊[9]运用有限元方法，研究了不同等级围岩的分界面及其与地面不同夹角情况下，初期支护、二次衬砌的内力变化以及配筋计算。刘科[10]通过数值模拟的方法对层状岩体和非均质岩体中围岩和衬砌力学特性加以分析，并结合实际工程进行优化。邵远扬[11]采用数值分析的手段针对层状岩体隧道围岩的破坏模式进行了分析。杨帆[12]等通过现场试验、理论分析和数值模拟等方法对急倾斜软硬互层围岩下洞室的变形破坏机理进行了研究。

目前，尽管对于偏压对盾构隧道衬砌结构的荷载和内力的影响规律均有分析，但对于非均质岩层引起的偏压情况研究较少，且不同区域地层差异较大，因此，为保证贵阳市轨道交通3号线盾构区间段施工安全，满足盾构隧道在运营阶段正常使用的需求，需对贵阳地区穿越岩层分层面的盾构隧道衬砌结构进行分析。本文选用二维平面模型分析不同岩层变形模量之比、不同分层面倾角与位置对盾构隧道衬砌结构受力的影响规律，据此为其他穿越非均质岩层的隧道建设提供依据。

1 工程概况

贵阳市轨道交通3 号线起点为花溪环城高速公路北侧的桐木岭站，终点为乌当区洛湾站，全长43.19km，其中地下线41.83km，高架线0.71km，过渡段0.65km。沿线以中风化白云岩、泥质白云岩、中风化“砂糖状”白云岩、灰岩等可溶性碳酸盐为主。3号线一期工程拟建盾构隧道内径5.5m，外径6.2m，管片环宽1.5m，管片厚度0.35m，接头采用弯螺栓，环、纵缝均不设凹凸榫。

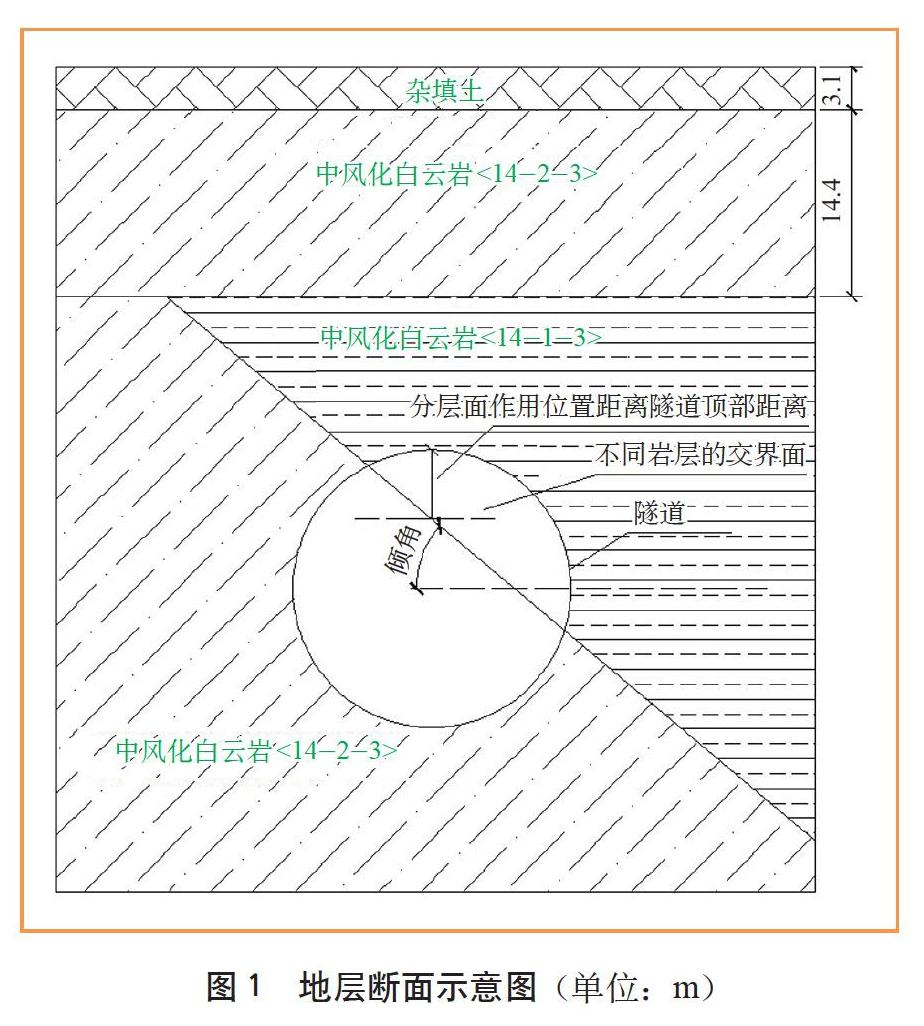
为分析非均质岩层分层面对盾构隧道的影响，本文最终取桃花寨—花溪南站区间段地层作为典型地层进行分析，具体分布情况见图 1。

2 数值模拟

2.1 参数选取

按照贵阳市轨道交通地勘报告并参考JTG D70-2004《公路隧道设计规范》附录A，本文模型参数取值见表1～表3。

2.2 模型假设

（1）不考虑由于地形偏压引起的偏压作用的影响，即取地表面为水平表面。

（2）不考虑均匀岩层内的软弱面参数，仅考虑2种岩层的分层面作为整个地层软弱面。

（3）围岩采用各向同性、连续的弹塑性材料参数，采用Drucker-Prager屈服准则。

（4）初始地应力计算只考虑由于岩体自重引起的自重应力场，忽略构造应力场。

（5）岩层走向与隧道轴线平行，按二维平面应变考虑。

（6）不考虑地下水的影响。

（7）开挖后地层与衬砌完全协调变形。

2.3 单元选取

模型地层选用plane42单元，衬砌管片选用beam188单元进行模拟。对于非均质岩层的分层面，现如今一般有2种模拟形式：①用较薄的实体单元来模拟等厚度的节理，由于夹层的厚度很小，单元尺度太小，导致网格单元划分不规则或者单元数过多，造成求解困难;②用接触单元模拟无厚度节理，即将节理用1层附着在二维实体单元上的单元来模拟，从而不会对实体网格划分造成限制，但是建模过程比较繁琐。本文计算中，选用接触单元进行模拟。

2.4 计算模型及工况

有限元模型两侧与底部均取3D（D为隧道直径）作为边界，即模型宽度为40m，高度为46.8m;模型边界，上边界取自由边界，左右边界约束水平位移，底部边界约束竖向位移;采用二维平面单元模拟。有限元模型见图2。

模型工况中不考虑地层的应力释放，因此仅有2个工况：工况1（初始工况），存在有分层面的情况，计算初始地应力场;工况2（衬砌工况），直接开挖地层并完成盾构衬砌圆环拼装。

结合实际地勘报告，为探究分层面上下岩层的变形模量之比、分层面倾角与分层面位置对衬砌结构受力的影响，选取实际模型计算工况见表4。表4中，分层面位置为距离隧道顶部的距离;上下岩层变形模量相对比值=右上侧巖层变形模量/左下侧岩层变形模量。

3 数值模拟结果分析

3.1 上下岩层相对弹性模量分析

（1）当上下岩层的变形模量比值为1时，通过图 3a、图 3b可以看出，衬砌弯矩略有降低，最小轴力会小幅度提升，整体受力还具有一定的对称性;而当上下岩层的变形模量比值逐渐减小，即上软下硬，内力分布会出现明显的不对称情况，最大正弯矩出现在顶部偏右位置，最大负弯矩出现在右侧腰部;通过图3b、图3c可以看出，最大轴力出现在左侧腰部，最小轴力出现在底部偏右位置，最大剪力出现在分层面穿过隧道的右下侧，且右上部还分布着较大的剪力，该趋势会随着上下岩层变形模量比值的降低而逐渐增强。

（2）当上下岩层的变形模量比值小于1时，整体来看受力不再对称，轴力偏向于靠近岩层弹性模量更大的管片左下部，弯矩偏向于靠近岩层弹性模量更小的管片右上部。

3.2 分层面倾角对衬砌受力影响分析

（1）衬砌最值弯矩截面分析。结合图4a弯矩图与表5最值弯矩及其相应轴力数据可以看出，对于最大正弯矩所在截面，其弯矩值在分层面倾角30～70°范围内与分层面倾角成正相关，从180.3kN · m增至257.4kN · m，且均超过了无分层面的情况，此时衬砌最大正弯矩位置对应的轴力从889.8kN降至523.1kN;对于最大负弯矩所在截面，随着倾角的增大，最大负弯矩值先增大后降低，在分层面倾角为50°的情况下，最大增至295kN · m，此时最大负弯矩位置对应的轴力从1530kN降至870kN。可见，弯矩增加而轴力降低，这意味着出现分层面的最值弯矩截面较无分层面的受力状态更加危险。

（2）衬砌最值轴力截面分析。结合图4b轴力图与表5最值轴力及其相应弯矩数据可以看出，随着倾角的增大，左侧的轴力逐渐增大，右侧的轴力则逐渐减小。对于最大轴力所在截面，当分层面倾角大于30°时，最大轴力与倾角成正相关，且随着分层面倾角的增大而增大，从1.797MN增至3.227MN;对于最小轴力，当分层面倾角在30°～60°时，最小轴力基本维持着500kN左右，当倾角大于60°时，最小轴力出现明显的减小趋势，最低降至315kN，当倾角大于40°时，最小轴力对应的弯矩随着倾角的增大而增大，最大增至252kN · m，达到了无分层面状态下弯矩的3倍。这意味着出现分层面的最小轴力截面较无分层面受力状态更加危险。

（3）衬砌最值剪力截面分析。结合图4c剪力图可以看出，衬砌结构的最大剪力出现在分层面穿过隧道的右下侧，同时右上部也会有一片较大的剪力分布。分层面倾角小于60°时，最大剪力会随着倾角增大而增大，最大增至-555kN;分层面倾角大于60°时，剪力数值会随着倾角增大而减小，降至-380kN。管片其他位置剪力分布同无分层面情况相近。

（4）最大拉应力分析。结合表5相应拉应力数据可以看出，随着分层面倾角的增大，衬砌结构上的拉应力逐渐增大，但最大拉应力出现的位置并不是不变的。无分层面的情况下，最大拉应力出现在顶部，为6MPa，而随着倾角的增大，最大拉应力的位置逐渐沿着顶部—右腰部—底部的路径转移（最大拉应力对应位置中的角度表示：0°为顶部，-90°为右侧腰部，90°为左侧腰部，180°/-180°为底部，下同）。

3.3 分层面位置对衬砌受力的影响

（1）衬砌最值弯矩截面分析。结合图5a弯矩图与表6最值弯矩及其相应轴力数据可以看出，对于最大正弯矩所在截面，弯矩随着分层面位置的下降而增加，最终达到281.9kN · m，超过无分层面情况的48%;最大正弯矩位置对应的轴力从1036kN降至474.2kN;对于最大负弯矩所在截面，截面位置一般位于右侧腰部，当分层面的位置处于隧道底部时，左侧肩部也会有较大的负弯矩;随着分层面位置的下降，最大负弯矩也逐渐增加，而当分层面位置大于0.5D后，最大负弯矩基本不变化，维持在280kN · m左右;最大负弯矩位置对应的轴力从1714kN降至1354kN。可见，弯矩增加而轴力降低，这意味着出现分层面的最值弯矩截面较无分层面的受力状态更加危险。

（2）衬砌最值轴力截面分析。结合图5b轴力图与表6最值轴力及其相应弯矩数据可以看出，对于最大轴力所在截面，最大轴力数值随着分层面位置的下降而降低，最多降低15%，当分层面位置大于0.5D后，最大轴力对应的弯矩随着分层面位置的下降而增大，最大增至-255kN · m，达到无分层面状态的2.5倍;对于最小轴力所在截面，随着分层面位置的下降，最小轴力数值随之降低，最多降低48%，当分层面位置大于0.25D后，最小轴力对应的弯矩随着分层面位置的下降而增大，最大增至132.7kN · m，达到无分层面状态的2倍。这意味着当分层面的位置从衬砌顶部降至底部时，衬砌的受力越来越危险。

（3）最大拉应力分析。结合表6相应拉应力数据可以看出，对于倾角为40°的分层面，当分层面位置大于0.25D后，其最大拉应力会超过无分层面的最大拉应力，且其值会随着分层面位置的下降而增加。值得注意的是，当分层面位置贴近顶部与底部时，最大拉应力出现的位置主要在顶部靠右侧，当分层面位置在衬砌环中部时，最大拉应力的位置会转移到右侧腰部附近。

4 结论

（1）当隧道穿越的岩层分层面上下岩层的变形模量相差较小时，该岩层分层面几乎不会对结构造成影响。而当两者有明显差别时，衬砌整体内力不再对称，轴力偏向于弹性模量更大的左下部，弯矩更偏向于弹性模量更小的右上部，结构受力逐渐倾斜。该倾斜的趋势会随着分层面倾角的增大而更加明显

（2）分层面的出现会降低最大正弯矩和最大负弯矩2种截面对应的轴力，同时会增加最小轴力位置处对应的弯矩，导致相应截面的内力状态与无分层面的工况相比更加危险，并且该状态会随着倾角的增大而变得更加危险。

（3）随着分层面位置的下降，最大正弯矩不断增加，最终超过无分层面情况的48%。同时衬砌的最大负弯矩也在逐渐增加，位置超过0.5D后，数值维持在无分层面情况的2倍左右。

（4）随着分层面位置的下降，最大轴力和最小轴力的数值都在相应降低，最大轴力最多降低了15%，而最小轴力则最多降低了48%。

（5）从最大拉应力的角度来看，随着分層面倾角的增大，衬砌结构上的拉应力逐渐增大，达到无分层面情况的2倍，最大拉应力的位置也逐渐沿着顶部—右腰部—底部的路径转移;随着分层面位置的下降，最大拉应力的值也在不断增加，最多增至2倍，最大拉应力的位置沿着顶部偏右侧—右腰部—顶部偏右侧移动。

参考文献

[1]何金刚.浅埋顺层偏压软弱围岩隧道施工变形控制技术[J].国防交通工程与技术，2014，12（3）：49-52，70.

[2]孙伟亮.顺层偏压地层隧道施工力学行为分析[J].铁道建筑技术，2008（5）：72-75.

[3]何振宁.铁路隧道疑难工程地质问题分析——以30多座典型隧道工程为例[J].隧道建设，2016，36（6）：636-665.

[4]孟祥马.顺层偏压地层下隧道稳定性分析[J].交通世界，2016（1）：64-66.

[5]冯立君.盾构穿越上软下硬地层施工技术措施[J].现代城市轨道交通，2016（2）：71-73.

[6]任桂兰.单线铁路隧道地质顺层偏压衬砌结构的试验研究[D].四川成都：西南交通大学，2004.

[7]周晓军，高杨，李泽龙，等.地质顺层偏压隧道围岩压力及其分布特点的试验研究[J].现代隧道技术，2006（1）：12-21.

[8]邓彬.地质顺层偏压隧道偏压作用的数值分析[D]. 四川成都：西南交通大学，2007.

[9]王磊.地质偏压隧道围岩压力分布及衬砌安全性的分析[D].四川成都：西南交通大学，2008.

[10] 刘科.层状与非均质岩体中隧道围岩变形和衬砌结构力学特性研究[D].四川成都：西南交通大学，2016.

[11] 邵远扬.层状岩体隧道围岩稳定性及破坏模式研究[D].四川成都：西南交通大学，2013.

[12] 杨帆，陈卫忠，郑朋强，等.急倾斜软硬互层巷道变形破坏机制及支护技术研究[J].岩土力学， 2014，35（8）：2367-2374.

收稿日期 2019-09-27

责任编辑 朱开明