含夹矸煤层滚筒磨损特性离散元模拟试验分析

赵丽娟，金 鑫，赵宇迪，王 斌

(辽宁工程技术大学 机械工程学院，辽宁 阜新 123000)

滚筒作为采煤机的工作机构，截割赋存条件复杂煤层时极易出现磨损失效，给整机工作可靠性和高效截割造成严重影响[1]，因此研究滚筒与煤岩相互作用过程中磨损特性，对提高其使用寿命意义重大。目前，已有国内外专家学者展开相关研究:刘晓辉[2]建立了镐型截齿与煤岩相互作用接触模型，以截齿与煤岩的干涉量为分析指标，研究截割形式、结构参数和工作角度对截齿磨损特性的影响规律。张强等[3-4]采用小波包分析、神经网络等方法，建立截齿磨损识别模型，实现截齿磨损状态的在线监测和磨损程度的快速准确识别;赵洪盛[5]提出一种改进的聚焦形貌算法，用于测量计算截齿磨损体积，准确率高达95%;DEWANGAN等[6-7]通过采用扫描电子显微镜和能量弥散X射线探测器深入研究截齿磨损部位，对截齿磨损机理进行了分类。史秀宝等[8]在MATLAB环境下模拟了滚筒齿座与煤壁间的干涉，找出了末端齿座磨损原因，有助于滚筒的结构优化;卜庆辉等[9]分析了滚筒齿座、螺旋叶片尾端磨损原因，并给出了改进方案;赵丽娟等[10-11]对截齿磨损、折断等失效形式进行总结分析，并从材料、加工工艺、结构设计等方面提出了相应改进措施。罗晨旭[12]提出一种基于SUSAN边缘检测算法的图像处理方案来获取截齿磨损面轮廓尺寸信息，研究了煤岩界面位置形式对截齿磨损的影响规律。

以上研究主要侧重于滚筒磨损机理和磨损程度识别等方面，对滚筒磨损程度的定量分析、因素影响规律等尚未进行深入探讨。笔者采用EDEM离散元数值模拟方法，以MG2×55/250-BWD型采煤机螺旋滚筒为工程对象，创建滚筒截割含夹矸煤层耦合模型，分析了滚筒磨损机理，研究了采煤机牵引速度、滚筒转速、螺旋升角和煤岩抗压强度对滚筒磨损的影响规律，并建立截齿、螺旋叶片磨损数学模型。基于实际工况，综合考虑截割比能耗、载荷波动系数、生产率，确定了滚筒最佳工作参数，为滚筒磨损问题研究提供了方法指导，对实际工况下滚筒磨损程度预测及截割参数选取提供参考，具有一定工程应用价值。

1 理论背景

1.1 镐型截齿力学模型

采煤机截割、破碎含夹矸煤层时，镐型截齿受力如图1所示。

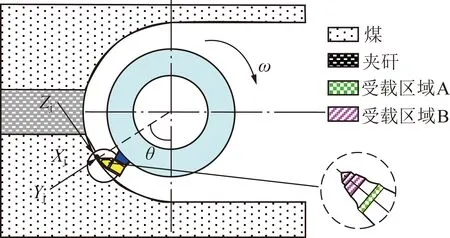
图1 滚筒单齿受力分析[13]

截煤时，截割阻力和牵引阻力分别[14]为

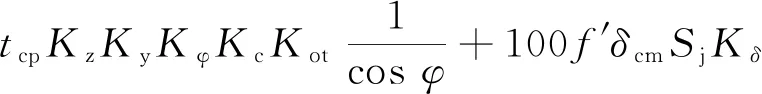
(1)

Yj=(0.5～0.8)Zj

(2)

截割夹矸时:截割阻力和牵引阻力分别为

Zj=PKkTkψk′ψkdk′y(0.25+1.8hmaxsinθtcp)+

PK0.1Sj

(3)

式中，PK为岩石的接触强度，MPa;kT为截齿类型系数;kψ为硬质合金头形状系数;k′ψ为刀头部形状系数;kd为硬质合金刀头直径系数;k′y为截齿截角影响系数。

Yj=2.5Zj(0.15+0.000 56PK)/(10hmaxsinθ)0.4

(4)

侧向力可由截割阻力表示为

(5)

式中，Xj为侧向力，N;Ci为截齿排列方式影响系数(i=1,2,3)。

1.2 螺旋叶片与煤岩颗粒间力学模型

滚筒装煤过程中，破落的煤岩颗粒随叶片共同运动，两者间的力学耦合作用十分复杂。由于颗粒质量较小，忽略其自身重力的影响[15]，为简化研究，依据散体力学理论，对单体煤岩颗粒进行受力分析，如图2所示。

图2 螺旋叶片与煤岩颗粒间力学分析

煤颗粒平衡方程为

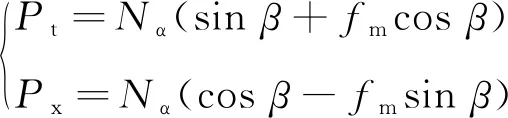
(6)

式中，Pt,Px分别为落煤切向力和轴向抛煤力，N;Nα为抛煤时螺旋叶片对煤颗粒的正压力，N;fm为螺旋叶片与煤颗粒的摩擦因数;β为叶片螺旋升角，(°)。

根据落煤切向力与煤岩颗粒切向分速度求得装煤功率为

NZ=0.001Nαvt(sinβ+fmcosβ)

(7)

式中,NZ为装煤功率，kW;vt=πnDsinβsin(β+ρm)/cosρm，ρm为摩擦角，(°);vt为煤岩颗粒切向分速度，m/min;D为颗粒所在叶片作用处的平均回转直径，m;n为滚筒转速，r/min。

装煤功率亦可表示[16]为

NZ=0.1vqvjKzm/n

(8)

式中，vq,vj分别为牵引速度和截齿截割线速度，m/s;Kzm为装煤阻力系数，N/cm。

联立式(7)，(8)可得到煤颗粒的正压力为

(9)

1.3 磨损模型

截割、装载过程中，煤岩体作为硬质颗粒对滚筒材料表面不断挤压，并存在相对运动，造成滚筒严重磨损，由磨损机理可知两者间磨损类型为磨粒磨损[17]。EDEM中Hertz-Mindlin with Archard Wear模型是基于J.F.Archard磨损理论[18]，对Hertz-Mindlin(no slip)模型的扩展，可用于设备磨损区域表面磨损深度值的求解，因此本文用以研究滚筒磨损问题。

根据J.F.Archard磨损模型可知，滚筒磨损量与载荷及材料之间的关系为

V=KFL/H

(10)

式中，V为磨损体积，mm3;K为磨损常数;F为接触载荷，N;L为相对滑动距离，mm;H为材料硬度。

定义W=K/H，则EDEM中滚筒表面磨损深度值为

h=WFL/A

(11)

式中，h为磨损深度，mm;A为接触面积，mm2。

2 EDEM离散元仿真模型建立

虚拟煤壁模型的构建是滚筒磨损离散元数值模拟试验的关键，为使虚拟煤壁更加接近实际，保证模拟结果的可信度，对兖州矿区杨村矿煤层进行取样，通过试验(图3)测定煤岩的物理、力学性质见表1。

图3 煤岩物理、力学性质测定试验

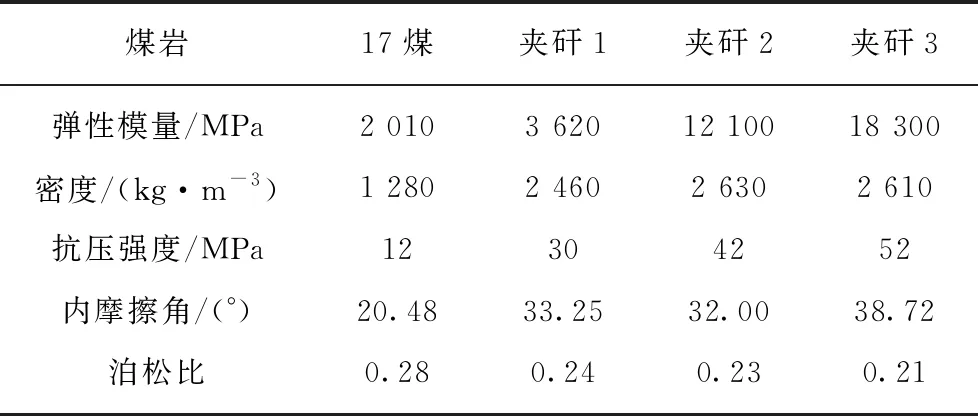
表1 煤岩试样物理力学性质

设置煤岩颗粒半径为12 mm，颗粒间接触模型为Hertz-Mindlin with bonding黏结模型，黏结参数可根据物理、力学性质测定结果，基于Hertz接触理论[19]，采用项目组开发的采煤机工作机构优化设计及载荷计算软件[20]计算得到，如图4所示。

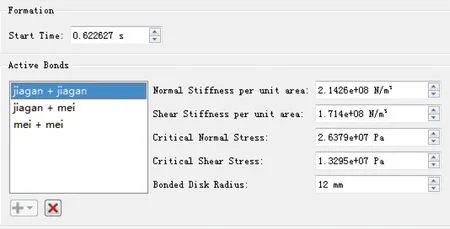
图4 颗粒间黏结参数

采用Pro/ENGINEER族表功能建立采煤机滚筒三维模型，进行网格划分后导入EDEM中，并根据需要建立夹矸层厚度为250 mm，整体尺寸为2 000 mm×800 mm×1 000 mm的煤壁模型[21]。设置颗粒与滚筒间接触模型为Hertz-Mindlin with Archard Wear模型。在Geometry模块下，通过Dynamics选项添加滚筒运动参数，根据现场工作条件，设置滚筒转速为72 r/min，牵引速度为4.2 m/min，最终得到离散元仿真耦合模型如图5所示。

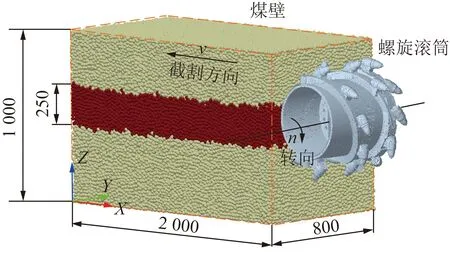
图5 EDEM仿真耦合模型

3 数值模拟结果分析

3.1 煤岩颗粒运动分析

利用EDEM后处理模块查看滚筒截割过程中颗粒运动状态，如图6所示。由图6可知，在滚筒截割作用下，外侧煤壁被截落的颗粒首先落入装煤区;内侧煤壁破碎后的颗粒首先在齿座根部附近形成堆积，在自身重力及螺旋叶片的推挤作用下，一部分沿滚筒轴线流向刮板输送机，一部分做抛物运动越过筒毂落入采空区，形成浮煤，且离滚筒越远，颗粒运动速度越大。

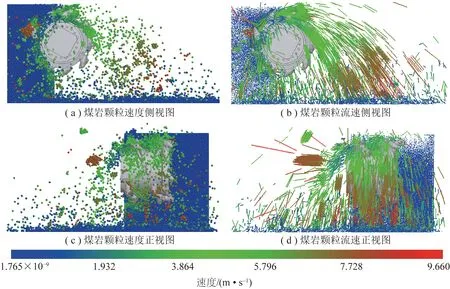
图6 滚筒动态截割过程颗粒运动状态

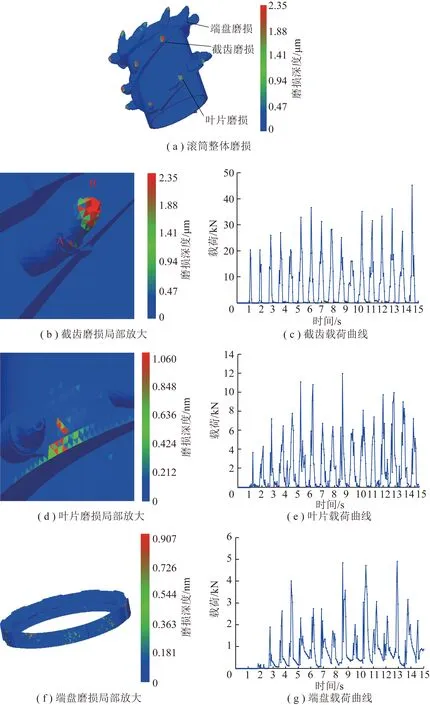
图7 滚筒组件磨损分布及载荷曲线

3.2 滚筒磨损分析

滚筒受煤壁和截落煤岩颗粒的共同作用，存在不同程度磨损。为便于观察，对滚筒主要磨损部位进行局部放大处理，滚筒组件磨损分布图及载荷曲线如图7所示。

由图7可知，滚筒组件中，截齿磨损最为严重，载荷峰值为45.15 kN，最大磨损深度为2.35 μm，磨损区域主要为合金头的齿尖局部接触区(受载区域B)及齿柄头部的轴肩处(受载区域A)，且受载区域B磨损程度大于区域A;叶片载荷峰值为12.03 kN，最大磨损深度为1.06 nm，磨损主要集中在尾片齿座根部附近位置;端盘载荷峰值为5.02 kN，最大磨损深度为0.907 μm，磨损主要集中在端盘端面和端部相邻齿座的空隙部位。这是由于截割过程中，截齿受载区域B与煤壁直接接触，存在较大接触力，并伴有相对运动，使得区域B受摩擦力作用明显，磨损最严重;滚筒装煤时，叶片与煤岩颗粒间存在推挤作用力，是其产生磨损的主要原因。而齿根附近煤岩颗粒的堆积使得该部位叶片受力较大，造成局部磨损相对严重;端盘位于滚筒的靠近煤壁侧，其与煤壁间的容煤空间较小。由端部截齿截落的煤岩颗粒部分落入容煤空间后受端盘和煤壁的不断挤压而继续破碎，部分在端部相邻齿座空隙部位堆积，由滚筒的不断转动随叶片排出，因此端盘端面与端部相邻齿座空隙部位受摩擦力作用较大，磨损程度较为严重。此外，滚筒和煤岩间复杂力学耦合作用产生的较大交变冲击载荷会引起滚筒的剧烈振动[22]，给滚筒组件带来不同程度的附加磨损。

3.3 可行性验证

由于现场工况下，滚筒磨损试验用时较长，且受EDEM计算速度的限制，采用离散元模拟方法进行定量化验证存在很大难度。因此，根据文献[23-24]中仿真模型的验证方法及文献[25]中截齿磨损的试验研究，文中通过对比仿真结果与现场磨损中(图8)滚筒磨损部位和特点，发现滚筒磨损情况具有一致性，证明了采用EDEM模拟滚筒截割复杂煤层进行力学分析及磨损研究是准确可靠的，具有可行性。

图8 螺旋滚筒现场磨损情况

4 滚筒磨损特性多因素影响分析

滚筒落煤与装煤是多因素耦合作用过程，其载荷具有非线性、时变性和强耦合性[26]。单一的理论分析并不能直接反映各因素对滚筒磨损的具体影响，笔者采用正交试验法探究不同工况下滚筒磨损规律。

4.1 试验设计

采煤机运动学参数、滚筒结构参数及煤岩物理、力学性质等共同决定滚筒的载荷特性[27]，与滚筒磨损情况密切相关。选取采煤机牵引速度、滚筒转速、螺旋升角、煤岩抗压强度为设计因素，按照L9(34)正交表进行模拟试验，分析其对滚筒磨损的影响趋势，因素水平表见表2。

以滚筒截齿、叶片磨损深度为试验结果，利用EDEM离散元软件进行仿真模拟，试验方案及结果(取5位有效数字)见表3，其中A,B,C和D分别为v,n,β和δ编码。

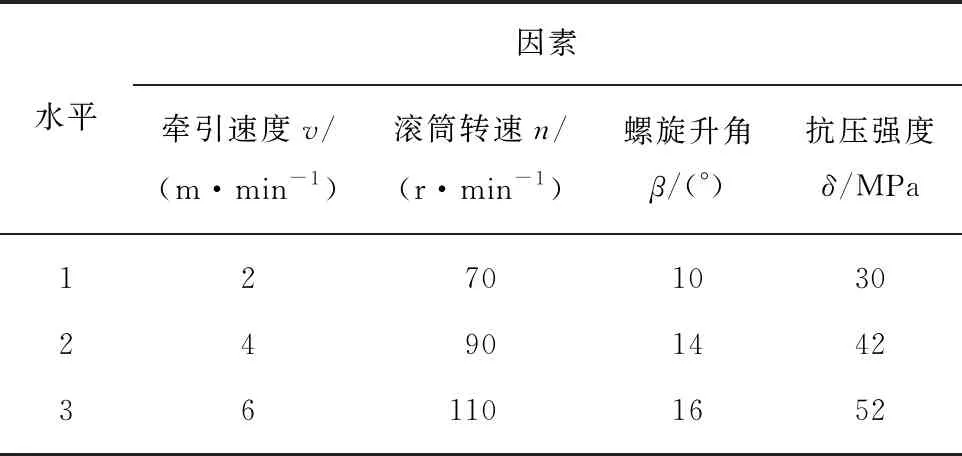
表2 因素水平[2]

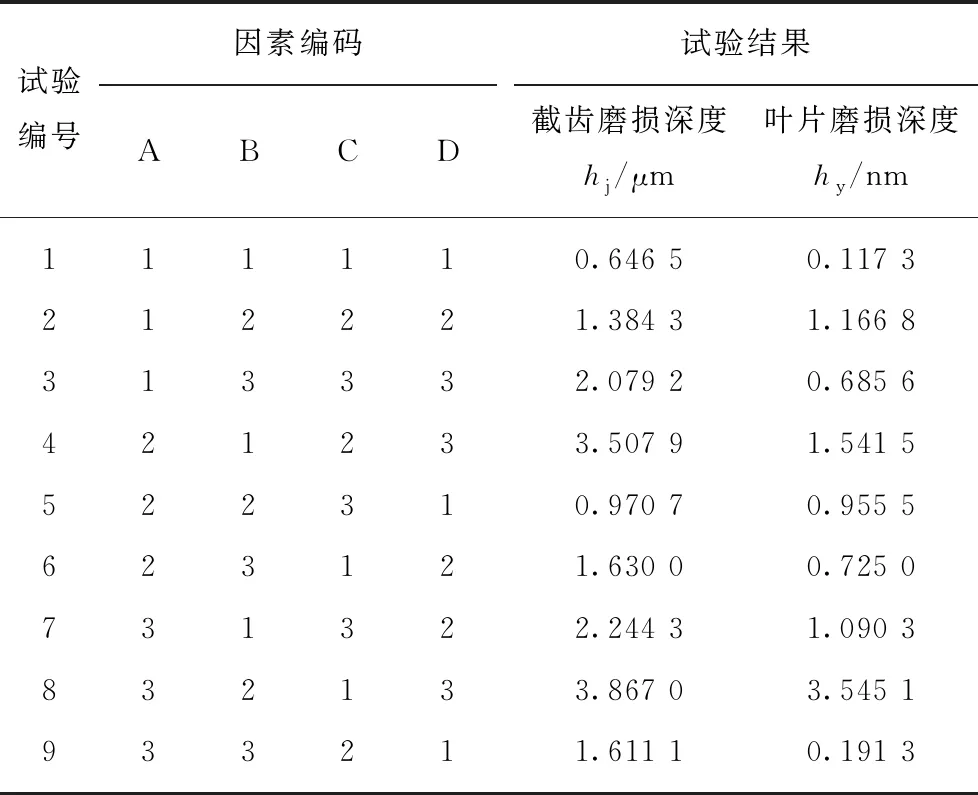
表3 试验配置方案及结果

4.2 结果分析

4.2.1极差分析

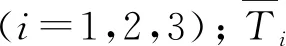
对比表4中截齿磨损数据:R(D)>R(A)>R(C)>R(B),S(D)>S(A)>S(C)>S(B)，根据极差分析原理[29]可知，煤岩抗压强度是其磨损的主要影响因素，影响高度显著，牵引速度次之，滚筒转速的影响最小;对比叶片磨损数据，R(D)>R(B)>R(A)>R(C),S(D)>S(B)>S(A)>S(C)，可知其磨损主要影响因素为煤岩抗压强度，影响最为显著，滚筒转速次之，螺旋升角的影响最小。

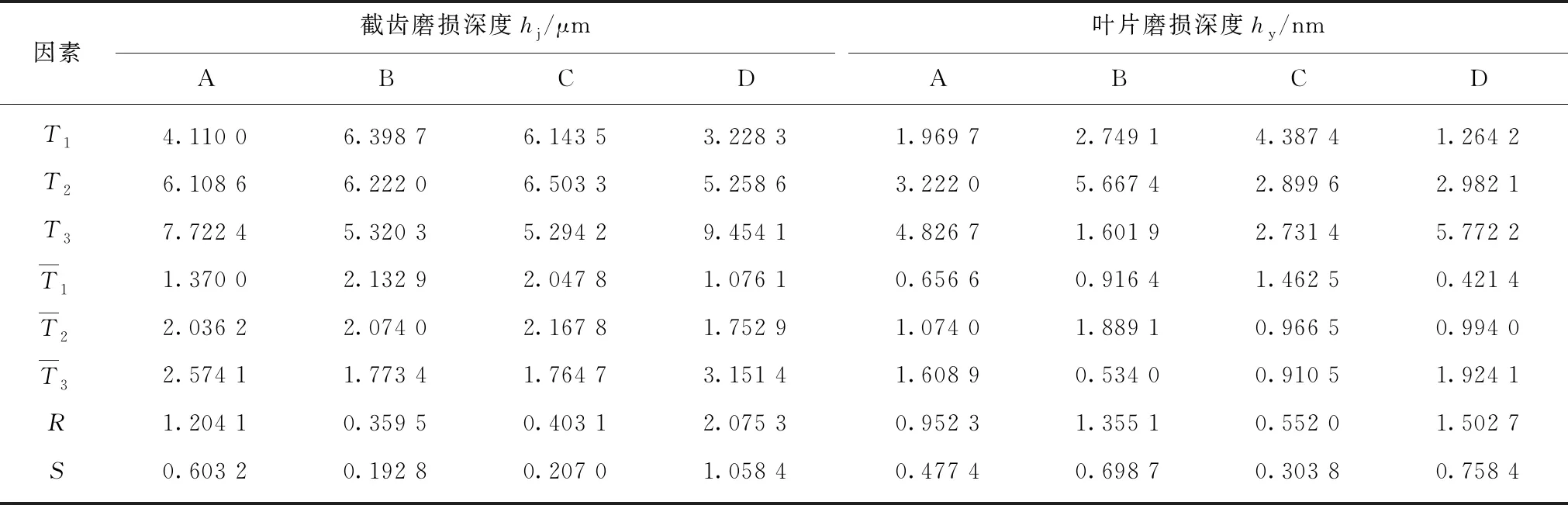
表4 截齿、叶片磨损深度极差分析

4.2.2因素影响趋势分析

以各因素水平为横坐标，截齿、叶片磨损深度均值为纵坐标，经过数据处理得到各因素水平趋势图如图9所示。

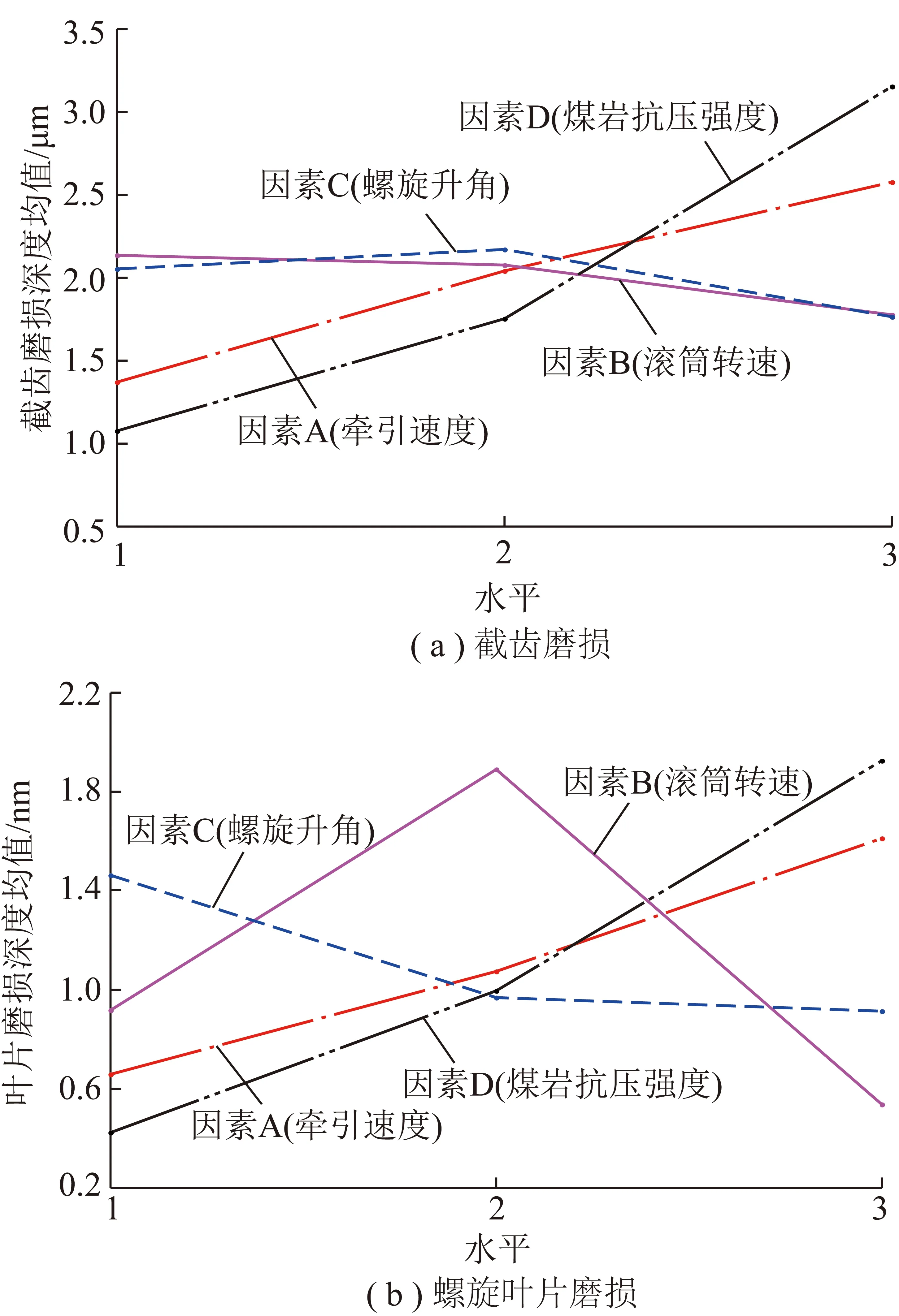
图9 截齿、螺旋叶片磨损因素水平趋势

分析图9可知:截齿、螺旋叶片磨损深度均随牵引速度、煤岩抗压强度增加而增加，但增加趋势有所不同。煤岩抗压强度增加，截齿、叶片磨损深度呈快速上升趋势，牵引速度增加则呈相对平缓上升趋势;随滚筒转速增加，截齿磨损深度逐渐减小，而叶片磨损深度先增加后减小;随螺旋升角增加，截齿磨损深度呈先增加后减小趋势，而叶片磨损深度逐渐减小。

呈现上述变化趋势的原因是:牵引速度增大，单位时间内截齿截割厚度、滚筒内煤流质量增加，导致单齿受力、叶片与煤流间摩擦力增加，从而加剧截齿、叶片磨损程度;滚筒转速增加时，煤岩的破碎程度较高，细碎、小块状煤体增多，使得煤体与叶片的接触面积增大，摩擦现象显著;当滚筒转速增大到一定值时，截落的煤岩颗粒大部分会越过筒毂落向采空区，使得叶片输送的煤流质量减小，从而减轻磨损程度;螺旋升角改变时，截齿相对位置、截割顺序与截割时间发生变化，导致大块煤随机崩落，截齿受力呈不规律变化;螺旋升角增加时，煤流颗粒轴向速度增大，叶片输煤能力增强，叶片与煤流颗粒间作用力减小，磨损程度降低;煤岩抗压强度越大，滚筒破碎煤岩体越困难，因此磨损越严重。

4.2.3最优方案确定

以滚筒截割夹矸抗压强度为30 MPa的工况为例，基于SPSS软件，采用数理统计方法对正交试验结果进行多元回归分析，分别得到截齿、叶片磨损深度评价模型:

hj=-7.546 6+0.429 3v+0.045 39n+0.956 0β-

0.016 03v2-0.000 302n2-0.038 58β2

hy=-18.440 7+0.120 6v+0.514 2n-0.507 8β+

0.014 68v2-0.002 910n2+0.015 99β2

以牵引速度、滚筒转速、螺旋升角为设计变量，截割比能耗Hw、载荷波动系数σ、截齿磨损深度hj、叶片磨损深度hy最小，生产率Q最大为多目标优化函数，考虑到各单目标的权重问题，对多目标函数进行规范化处理，转化后的目标函数为

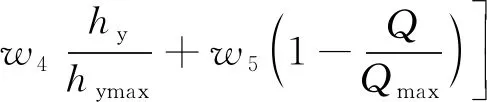
(12)

式中，各单目标函数具有同等重要地位，因此w1=w2=w3=w4=w5=0.2[30];采用项目组基于MATLAB及Excel联合开发的采煤机工作机构优化设计及载荷计算软件(2014SR102903)，在其中输入相关参数，根据计算结果进行拟合得到截割比能耗Hw、载荷波动系数σ和生产率Q函数模型[31];Hwmax,σmax,hjmax,hymax,Qmax分别为各单目标函数在论域中最大值。

采用MATLAB中Constrained nonlinear minimization求解器进行求解，设置初始解为[2 70 10]，迭代误差为10-6，得到优化函数最优解为(v,n,β)=(5.66,80.40,11.35)，即当牵引速度为5.66 m/min、滚筒转速为80.40 r/min、螺旋升角为11.35°时，滚筒性能达到最优，此时截割比能耗为0.713 2 kW·h/m3、载荷波动系数为0.081 9、截齿磨损深度为1.595 μm、叶片磨损深度为1.061 nm、生产率为315.465 5 t/h。

5 结 论

(1)基于煤岩物理、力学特性测试试验，利用EDEM离散元软件建立采煤机滚筒截割含夹矸煤层耦合模型，对滚筒磨损过程进行数值模拟，仿真结果与滚筒现场磨损情况具有一致性，验证了采用EDEM离散元法进行滚筒磨损模拟试验研究的可行性。

(2)利用EDEM数值模拟方法揭示了滚筒磨损机理，得出截齿齿尖主要磨损区域为受载区域B，叶片主要磨损区域为尾片齿座根部位置附近。

(3)基于EDEM滚筒磨损数值模拟，对采煤机牵引速度、滚筒转速、螺旋升角及煤岩抗压强度进行了四因素三水平正交试验，确定了因素影响显著性及影响趋势。基于实际工况，以截割比能耗、载荷波动系数、截齿磨损深度、叶片磨损深度、生产率为目标函数建立了多目标优化函数，得到了滚筒工作参数的最佳匹配，即当牵引速度为5.66 m/min、滚筒转速为80.40 r/min、螺旋升角为11.35°时，滚筒性能达到最优。

(4)离散元数值模拟方法实现了滚筒磨损的量化分析，为滚筒磨损问题研究提供了一种新的思路，极大地降低了试验成本，对研发高效、强力、耐磨滚筒具有借鉴意义。