基于长短期记忆网络的齿轮剩余寿命预测研究
2020-10-13王婉娜刘佳媛
石 慧,王婉娜,张 岩,刘佳媛
(太原科技大学 电子与信息工程学院,太原 030024)
齿轮作为机械设备的传动装置,其健康状况对设备的稳定性和寿命有很大的影响。现代机械设备随着集成度的提高,齿轮的精度也越来越高,在长期运行中很容易出现磨损,从而发生轮齿折断。监测齿轮的健康状态是保障机械设备可靠运行的重要手段。基于可靠性、经济性考虑,齿轮故障预测与健康管理(Prognostics And Health Management,PHM)[1]得到了越来越多的关注,其中,剩余寿命(Remaining Useful Life,RUL)预测是其核心研究内容。随着信息传感技术的发展,设备可监测点增多,信号采样频率增高,设备在运行过程中可获得海量的数据,进而推动PHM进入了大数据时代[2]。如何利用海量数据挖掘设备的状态退化规律,从而预测设备的剩余寿命,已成为预测与健康管理的一大挑战。
齿轮一般封装在齿轮箱中,借助传感器接收到的信息反映设备的退化状态。数据驱动的剩余寿命预测方法是基于统计学理论与人工智能理论,利用传感器获得表征设备状态退化的数据,实现实时剩余寿命预测[3-4]。刘颖等[5]利用时间序列ARMA(Auto regressive moving average)预测模型,根据模拟信号对汽轮机故障进行诊断,但ARMA预测模型适用于时间序列的短期预测和处理具有一定规律性的平稳性数据。WANG X等[6]提出支持向量回归(Support vector machines regression,SVR)和奇异谱分析(Singular spectrum analysis,SSA)相结合的方法对飞机齿轮箱的故障进行预测,利用SSA提取原始数据的特征值,分别建模预测齿轮箱的故障,取得了比单一模型更好的结果。但模型结构复杂,当样本数据量很大时,预测结果耗时。DAVIES T M等[7]采用人工神经网络(Artificial neural network,ANN)对柴油机涡轮增压器和汽车发动机的故障进行预测,利用遗传算法对ANN的网络结构参数进行优化。ANN中网络神经元起着关键作用,计算的复杂性取决于神经元的数目和隐藏层层数,若样本过多容易出现“维数灾难”,或出现“过学习问题”。
近年来,深度学习受到了广泛关注。深度学习[8-9]通过海量的训练数据构建具有很多隐层的神经网络模型,将样本在原空间的特征表示变换到一个新特征空间,逐层提取输入输出样本中潜在的映射关系。循环神经网络(Recurrent Neural Networks,RNN)[10]可将前面的序列输入进行记忆并应用于之后的计算中,但无法解决长时依赖问题[11]。长短期记忆网络(long short-term memory,LSTM)模型通过模型参数和控制信息流动的门控单元系统可避免梯度消失等问题,使得时序信息预测更加准确。Haitao Zhao[12]等将长短时期记忆网络应用在故障诊断方面,对故障进行分类,但是需要对数据进行经验模态分解,如果监测信号出现信号中断,将引起模态混叠不利于故障诊断。赵建鹏[13]等将长短时期记忆网络LSTM应用在旋转机械状态单步预测,取得比支持向量回归机更好的效果。王鑫[14]等将LSTM应用在飞机故障时间序列的预测上,通过与多种时许序列预测模型对比,LSTM具有很强的适用性和更高的准确性。
本文针对大数量级的序列预测,建立新的记忆机理循环神经网络实时剩余寿命预测模型,并从网络结构的搭建,学习率、窗口设置上改进网络模型预测的准确性。参数修正时采用加入Nesterov动量的随机梯度下降算法,防止陷入局部最优;采用RMSProps算法修正模型自适应率。最后,应用齿轮弯曲疲劳试验数据进行验证,并与时间序列预测模型对比,试验结果表明本文建立的新的记忆机理循环神经网络实时剩余寿命预测模型在剩余寿命预测上具有良好的优越性。
1 长短时期记忆循环神经网络
1.1 循环神经网络
循环神经网络是将深度学习扩展到序列数据预测的一类方法。如动态系统的经典形式:
s(t)=f(s(t-1),x(t);θ)
(1)
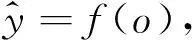
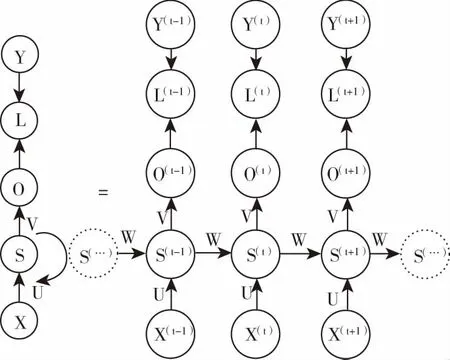
图1 RNN展开结构Fig.1 RNN expand structure
(2)
(3)
(4)
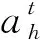
1.2 长短期记忆神经网络
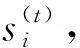
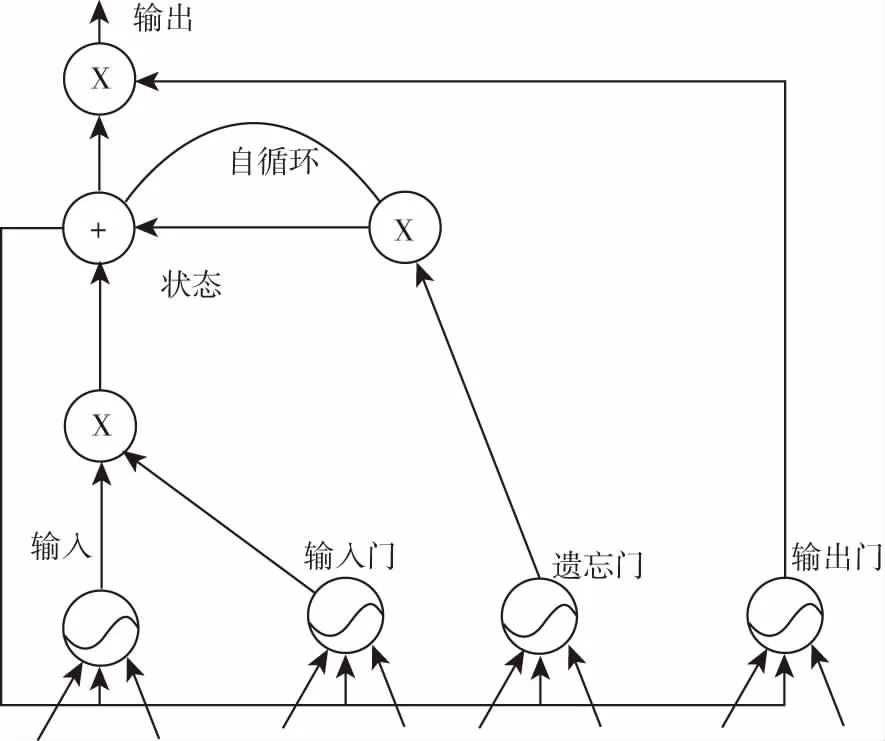
图2 LSTM结构图Fig.2 LSTM structure diagram
遗忘门移除LSTM学习不重要的信息,这些信息将通过门控单元运算移除。遗忘门采取两个输入ht-1和xt.相应的前向传播算法如下:
Input gates:
(5)
Forget gates:
(6)
Cells:
(7)
(8)
Output gates:
(9)
Cell outputs:
(10)
2 改进的基于记忆机理循环神经网络LSTM预测模型的参数优选
本文采用加入动量考虑的随机梯度下降算法优化模型参数,结合Nesterov动量的RMSProp算法自适应学习率,并利用随机搜索选择模型超参数。采用梯度下降法优化求解损失函数J(θ)极小值。
梯度下降法要在全部训练数据上最小化损失,当样本量非常大或是迭代次数加大时会非常消耗计算资源。随机梯度下降(Stochasitc Gradient Descent,SGD)优化损失函数通过计算梯度均值,求其最小化损失。SGD算法中关键的参数是学习率,在LSTM应用中会随着时间的推移逐渐改变学习率。
2.1 动量参数优化
随机梯度下降是深度学习中常用的优化算法,加入动量优化算法旨在加速学习,特别是对加噪声的梯度。动量将梯度累加,即更新的时候在一定程度上增加稳定性,从而加速学习,抑制震荡,具有跳出局部最优的能力,表示为:
xt+1=αxt-ηg
(11)
超参数α∈[0,1]决定了之前梯度的贡献衰减,通常设为0.5、0.9、0.99.本文使用Nesterov动量的随机梯度下降更新如表1所示:

表1 随机梯度下降Tab.1 Random gradient drop
2.2 自适应学习率算法
学习率对预测模型的性能有显著影响,决定了参数收敛到最优值的速度。学习率太小,收敛过程十分缓慢,容易引起运算冗余;学习率太大,会导致参数可能越过最优值,长时间运算无法收敛。目前常用的算法有AdaGrad[18]算法、RMSProp[19]算法和Adam[20]算法等,RMSProp算法在非凸设定下效果更好。本文采用结合Nesterov动量的RMSProp算法,引入新的超参数ρ,自适应改变学习率,求得最优值的同时提高收敛速度。

表2 RMSProp算法Tab.2 RMSProp algorithm
2.3 选择超参数
LSTM预测模型中包括了很多参数,其中以学习率,分割窗口,状态向量大小最为关键。最常见的参数优化方法为网格搜索和随机搜索。Bernoulli and Bengio[21]对比了网格搜索和随机搜索,网格搜索计算代价会随着超参数数量呈指数级增长,无法提供令人满意的搜索规模;本文采用的随机搜索可以替代网格搜索的方法,通过随机搜索可以发现数据在某一维上的变化更加明显,能更快的收敛到超参数的良好取值。
3 实例验证
3.1 疲劳试验台架
试验数据采用如图3所示齿轮疲劳寿命试验台的实时监测数据集。试验过程对箱体振动、油温和噪音等进行监测。

图3 齿轮试验台架Fig.3 Gear test bench
疲劳试验台主试箱传感器位置如图4所示。本试验共布置11个传感器,当试验齿轮发生断齿时即判定该齿轮失效。试验中齿轮安装采用正反面交错搭接啮合方式,采样频率25.6 kHz,采样时间60 s,采样间隔9 min.所采集信号为齿轮箱体的振动加速度信号。

图4 主试箱传感器位置图Fig.4 Main test box sensor location map
3.2 特征提取
选择合适的特征指标不但可以真实准确的反应齿轮在服役过程中的性能变化,而且易于计算。本文将均方幅值(Root Mean Square,RMS)作为特征值对齿轮磨损状态变化进行性能衰退评估。均方幅值作为有量纲的特征值[22],会随疲劳状态的累积呈现出递增趋势,能较好的反映采样时刻振动能量的变化情况。均方幅值可表示为:
(12)
式中,Δt为采样时间,Fs为采样频率,n为采样点数,n=Fs×Δt.在不同的退化状态,齿轮振动能量会有明显的变化。
数据的训练平台主要配置为:处理器XeonE5-2620 v2系列六核心,内存32 GB,显卡NVIDIA Tesla K20c,在本试验中采用GPU进行数据的训练和预测。
3.3 数据预测
采用本文建立的改进的基于记忆机理循环神经网络LSTM实时预测模型进行预测,选取最靠近主试验箱的4#加速度传感器接收到的振动数据均方幅值作为模型输入,结果如图5所示。
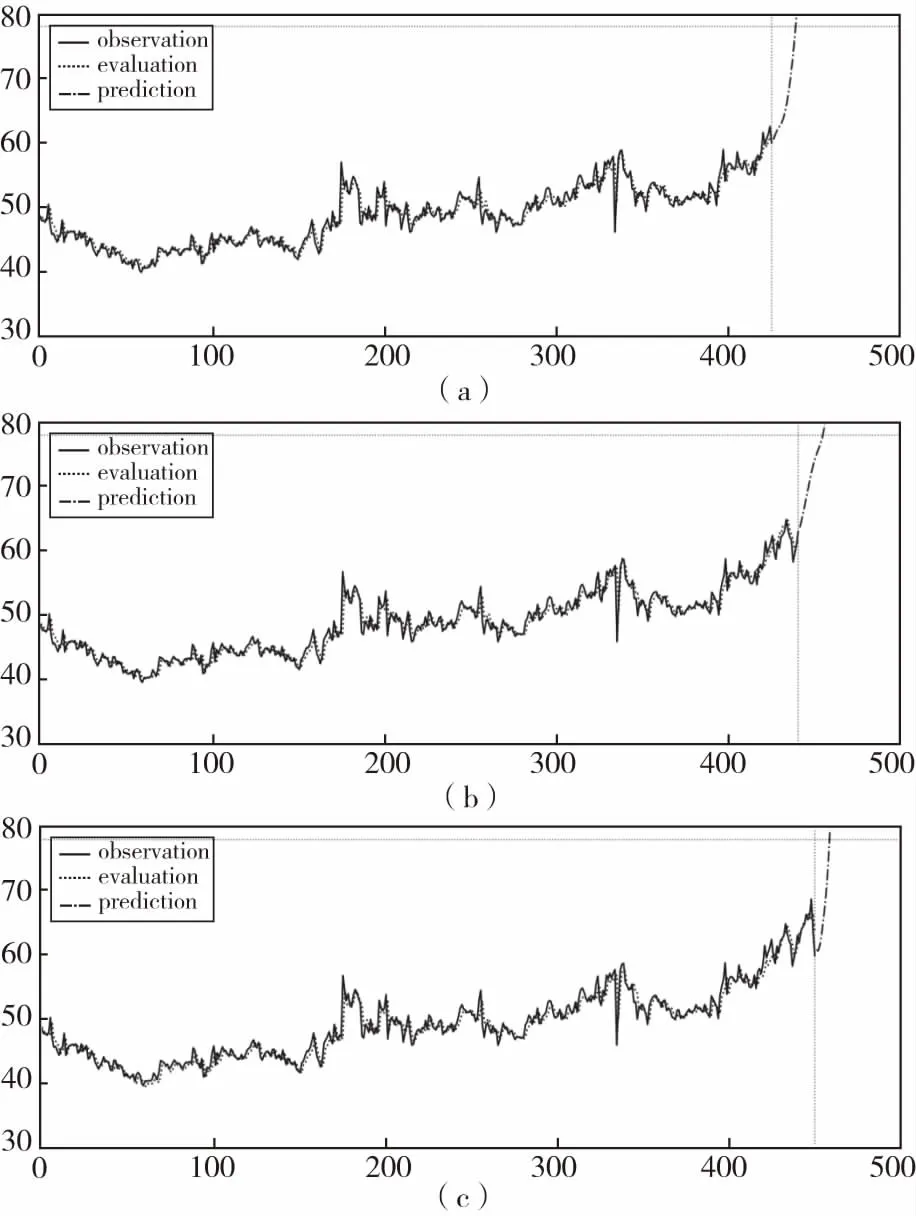
图5 (a)(b)(c)分别在70 h、73.3 h、75 h的预测效果Fig.5 Predictive effects in 70 h,73.3 h and 75 h respectively
横坐标表示采集的样本数,纵坐标表示齿轮退化状态,在预测时间点之前实线表示实际的观测值,在预测时间点之后的虚线表示预测结果。分别展现了模型在70 h、73.3 h、75 h的预测效果。
图6横坐标为模型的训练次数step=200,纵坐标表示训练误差loss。随着训练次数的增加,loss呈下降趋势,表明模型正在学习该预测问题并且具备预测能力。试验表明,LSTM在迭代300次左右开始收敛,下降速度变慢,说明其误差已经非常小,具备良好的预测能力。
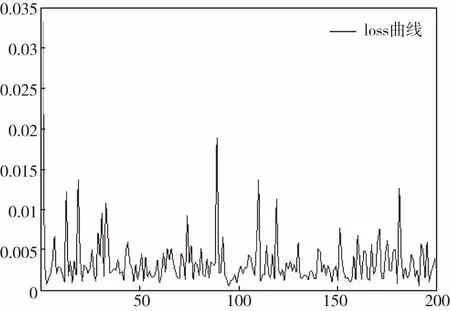
图6 LSTM训练误差下降曲线Fig.6 LSTM training error drop curve
为验证本文所提模型的准确性,与自适应回归模型(Autoregressive model,AR)预测效果相比较。如图7所示为AR模型预测效果,预测点之前实线表示实际的观测值,预测点之后虚线表示预测结果。

图7 AR模型预测效果Fig.7 AR model predictive effect
由试验可知,齿轮退化状态的阈值为76.375 mm/s2,T*=77.2 h为齿轮的实际故障时间。
齿轮的实际剩余寿命Ta为:
Ta=T*-tp
(13)
式中,tp表示当前时刻,T*为齿轮首次到达故障阈值的时间。
将采样点数折算成时间,引用相对误差百分比(Relative Percentage Error,RPE)
(14)
TRUL表示齿轮剩余寿命,模型的预测准确度(Prediction Accuracy,PA)为:
PA=1-ERPE
(15)
由表3所示的实际值与预测值之间的差异,可看出本文所提模型预测误差小,学习数据演变规律的能力较强。
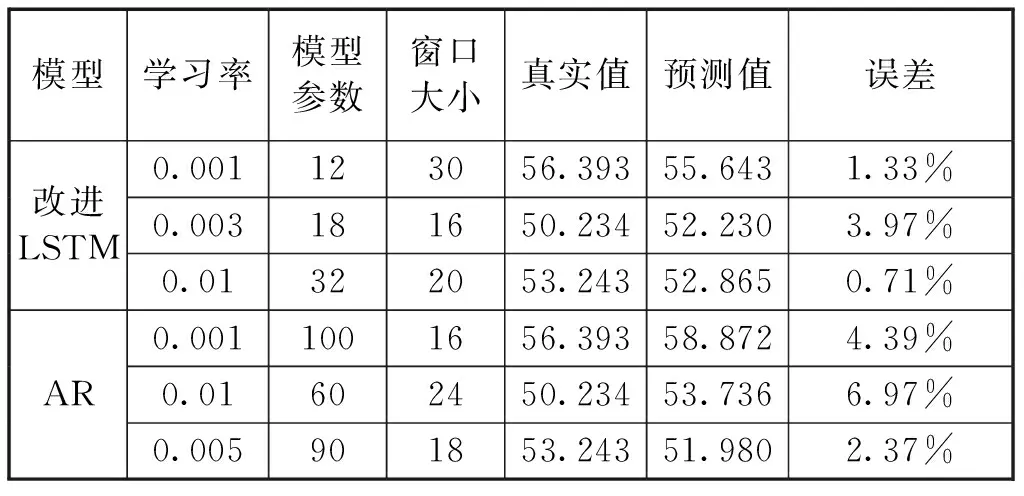
表3 预测数据与真实数据对比Tab.3 Comparison of forecast data with real data
本文建立的改进型记忆机理循环神经网络LSTM实时剩余寿命预测模型预测剩余寿命的准确度如下表4所示。试验表明,训练样本数据越多,预测准确度就越高。针对疲劳累积型数据的长距离预测,本文所提实时剩余寿命预测模型与ANFIS模型相比表现出明显优势。
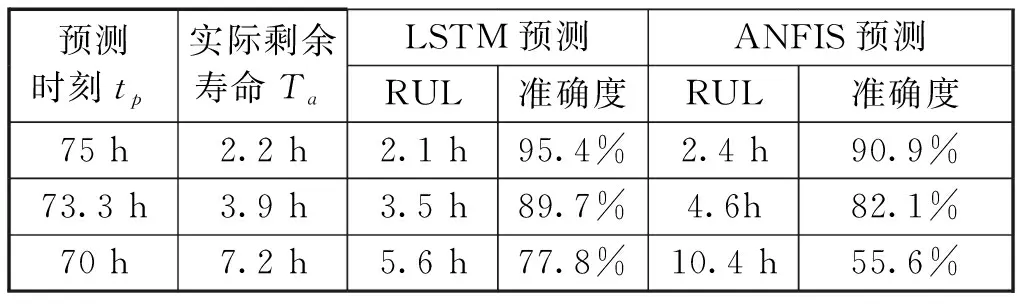
表4 模型预测准确度的比较Tab.4 Comparison of predictive accuracy of models
4 结论
本文通过研究齿轮振动数据特性,建立改进的基于记忆机理循环神经网络实时剩余寿命预测模型,并对预测模型参数进行优化,将预测模型应用于齿轮的剩余寿命预测研究中。结果证明本文建立记忆机理循环神经网络模型预测实时剩余寿命具有更高的准确度。下一步工作将多监测点的数据进行融合,研究其剩余寿命预测模型。
