等厚顺层岩质边坡稳定性的模型试验研究及数值验证

张 璟，陈文胜，蒋茂林

(1.新疆交通科学研究院 乌鲁木齐市 830000； 2.干旱荒漠区公路工程技术交通行业重点实验室 乌鲁木齐市 830000；3.长沙理工大学 土木工程学院 长沙市 410004)

0 引言

新疆天山区域、昆仑山区域面积辽阔，众多路线穿越深切河谷和峡谷陡坡坡角附近，周围山势陡峭，岩性复杂多变，公路路堑深边坡稳定性差，近些年来，国内外对层状岩质边坡稳定性的研究越来越重视，也取得了一些研究成果。

陈从新[1]以相似理论为依据进行了物理模型试验，研究了顺层岩石边坡的变形破坏机制以及边坡岩体的岩层倾角对边坡稳定性的影响；左保成[2]针对京珠高速公路某边坡原型进行了数组相似模拟地质模型试验,研究了岩层倾角、层面强度等因素对反倾岩质边坡稳定性的影响；蒋青青[3]利用有限元数值软件FLAC3D模拟层状三维遍布节理，研究分析了岩层倾向和坡角对边坡稳定性的影响规律；林杭[4]运用有限元数值软件FLAC2D模拟了层状岩体边坡在不同结构面倾角的稳定性。程东幸[5]以广西某水电站边坡工程的地质模型为工程背景，借助离散元软件3DEC模拟了结构体和层面不同影响参数对边坡稳定性的影响，提出了边坡反倾岩层优势角的范围。

以上研究主要是基于开挖扰动状态下的稳定性分析，对于未扰动的坡体稳定性的研究并不常见，且在数值分析方面多以有限元软件Flac2D,3D和离散元软件UDEC及3DEC为主，对于石华根博士提出的非连续变形理论分析方法DDA软件应用的并不多[6-7]。本文将以未扰动的等厚顺层岩质坡体为模型进行物理试验，研究其稳定性影响因素及失稳破坏机制，并结合DDA软件对物理试验工况进行数值模拟验证分析。

1 模型试验概况

1.1 试验模型设计

室内旋转边坡模型装置主要包括模型支架、旋转平台、抬升系统和测量系统。模型试验的基本模型如图1所示。

模型试验以天山公路某等厚层状岩体为原型，以现代地质力学理论和相似理论为基础，取Cl=100，Cγ=1.5。根据相似判据得相似条件如下：

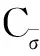
在实际模型试验中，并不能全部满足相似判据，只能是使其中的某些条件满足相似判据，从而进行试验模拟。由于原始边坡的岩层产状比较稳定,本试验在设计模型时选择统一的岩层倾角来进行模型试验。为了反映原始边坡的层状性质,同时考虑到模块制作的方便及模块性质的稳定性,试验所用模块尺寸为185mm×85mm×50mm和240mm×120mm×53mm的砖块,以砖块的厚度(50mm)模拟层状岩体的厚度，结构面的内摩擦角为33°，共10层。

1.2 试验方法

试验共分为4组，用两种大小不同的模块分别模拟两种节理密度分布的坡体稳定性试验，1至4组试验坡体依次为：小块体大密度节理、小块体小密度节理、大块体大密度节理、大块体小密度节理。将坡脚一端的最底层块体固定防止滑动，块体之间相互不粘结，以模拟岩体节理裂隙，将每组试验模型体边坡与岩层的夹角设为20°、25°、30°、35°、40°、45°六种不同工况，岩层的倾角随着模型体一端的转动抬升而不断增大，直至坡体失稳破坏。在模型坡体的临空地表坡面、模型坡体的中间部位及靠近坡体背面的重要部位布置了15个测点，其布置图及模型体安装图见图2。

小块体厚度均为50mm，其大密度节理间隙为185mm，小密度节理间隙为85mm；大块体厚度均为53mm，其大密度节理间隙为240mm，小密度节理间隙为120mm；内摩擦角均为33°，环境温度为(20±5)℃，相对湿度70%，块体力学参数如表1。

表1 岩体力学参数

2 试验过程及结果分析

2.1 边坡失稳过程的变形规律

图3(a)～图3(f)为小块体模型试验中边坡与岩层夹角20°至45°时倾角-位移曲线图，由图可以看出：

(1)当岩层倾角增大至某一角度时，坡体临空坡面上端部位的块体突然滑动，使坡体产生部分变形，暂停抬升倾角静置一会后坡体处于稳定状态，这说明坡体在发生破坏变形后产生了应力重分布，使坡体达到一个新的稳定状态。继续抬升倾角，增大至一定角度时，坡体发生整体破坏，分两次破坏的情况主要发生在图3(a)、图3(c)、图3(e)、图3(f)组坡体中，其余两组坡体都是一次性整体破坏。

(2)在发生第一次破坏前，无论是横向位移还是纵向位移，都是坡面上部9#测点的位移最大。由图表我们可以看出，岩层倾角越大，块体的变形速度越快，在坡面部位由上至下变形速度会逐渐减小，坡脚部位的变形速度最小，同样在坡体内部，下部的变形速度明显小于上部的变形速度，整个坡体变形速度最小的部位出现在坡脚处及坡体底部最上端。这说明顺层岩质边坡发生破坏，首先从边坡坡顶产生变形，以滑动拉裂破坏为主。

(3)边坡倾角抬升的过程中，边坡的形变并不一直是向下滑移，也会有向上突起的情况，因不同部位块体的下滑力和摩擦系数有所差异，当同一层靠上的块体产生的下滑力不足以推动下端的块体产生变形时，则会有向上突起的趋势，从而产生挤压变形。

(4)顺层岩体坡体的破坏主要以滑移破坏为主，并伴随有倾倒变形。在坡体发生滑动破坏时，上层块体下滑过程中的下滑力不足以抵消下层块体所带来的摩擦力时，动能传递至下层块体，从而产生了倾倒破坏。

(5)除了图3(b)组坡体，其余坡体发生破坏变形均是在岩层倾角大于层间内摩擦角时，这说明岩层倾角大于内摩擦角是层状坡体产生破坏变形的主要条件之一。

2.2 节理密度对边坡稳定性的影响规律

对四组试验数据进行处理，第1、第2组小块体试验破坏及变形曲线如图4(a),第3、第4组大块体试验破坏及变形曲线如图4(b),试验中没有发生两次破坏的该组数据未放入图中。

(1)两组试验中小密度节理坡体破坏时的倾角均大于大密度节理坡体破坏时的倾角，说明节理裂隙密度对边坡的稳定性影响较大，同一坡体中，节理裂隙密度越小，边坡越稳定。

(2)相较于第1组大密度节理坡体试验，第2组试验中坡体破坏时的岩层倾角曲线更为平稳，保持在36°附近，没有出现较大的波动。同样在第3、第4组试验中破坏曲线也没有大的波动，因此将第1组试验30°夹角的坡体与其他组试验坡体对比，30°夹角坡体的各层节理裂隙连续、几乎完全贯通，走向与岩层的夹角为88°接近垂直，各层块体之间缺乏咬合作用力，因此，在岩层倾角仅为26.8°时就发生了倾倒破坏。而其他三组试验的节理裂隙分布更均匀，没有出现完全贯通节理，推测第1组试验中30°坡角首先发生破坏的原因是由于贯通节理造成的。

(3)观察试验中首次变形和最终破坏时岩层倾角曲线，发现两组曲线的波动走向一致，这说明坡体稳定性受岩体结构面的影响较大,受坡角的影响并不明显。

2.3 岩层倾角对边坡稳定性的影响规律

对第1组试验数据处理，生成50°和55°坡角时的倾角位移曲线如图5、图6。

由图5、图6分析：

(1)当坡角一样时，无论是横向位移，还是纵向位移，都是随着岩层倾角的增大而增大。这说明当相同坡角的坡体，在内摩擦角相同时，岩层倾角越大越容易产生破坏变形，坡体稳定性越小。

(2)在坡角一样的坡体中，节理的贯通性比岩层倾角对坡体的稳定性影响大。

3 DDA数值模拟验证

3.1 岩质边坡模型主要参数

设定岩层倾角为30°，岩层与坡面的夹角为45°，块体尺寸为100mm×50mm×80mm，即岩层厚度为50mm，节理间隙为100mm。模型如图7所示。

以前面所做物理模型试验为算例，沿用物理力学参数和结构面参数，内摩擦角设为30°便于建模，具体参数见表1、表2。

表2 结构面力学参数

3.2 数值模拟分析

对坡面及坡体内部共设置了6个位移监测点，监测其横向和纵向位移，具体数据处理如图8。

我们进行了坡面、坡顶和坡体内部位移速度的相互对比：

(1)由各个测点的位移-时间图我们发现，无论是横向位移还是纵向位移，都是坡面顶端位移最大，变形速度最快。

(2)在坡面部位由上至下变形速度会逐渐减小，坡脚部位的变形速度最小，同样在坡体内部，下部的变形速度明显小于上部的变形速度，整个坡体变形速度最小的部位出现在坡脚处及坡体底部最上端。这说明顺层边坡的变形破坏首先发生在临空面靠近地表部位，产生拉裂破坏。

4 结论

(1)顺层岩质坡体发生的破坏主要受岩层倾角和节理裂隙两大因素影响，在节理分布情况较好，即贯通性节理少时，坡体发生整体破坏的主要条件是岩层倾角大于结构面内摩擦角，但是在岩层倾角小于内摩擦角时坡体也有可能发生局部变形，主要表现在坡顶岩层滑动破坏；在岩体中节理贯通性好时，坡体的稳定性将主要受节理条件影响，贯通性节理越大，边坡越不稳定。

(2)等厚顺层岩质边坡发生第一次破坏前，无论是横向位移还是纵向位移，都是坡面顶部附近的位移最大。在发生破坏变形的过程中，坡面部位由上至下变形速度会逐渐减小，坡脚部位的变形速度最小，同样在坡体内部，下部的变形速度明显小于上部的变形速度，整个坡体变形速度最小的部位出现在坡脚处及坡体底部最上端。这说明顺层岩质边坡发生破坏，首先从边坡坡顶产生变形，以滑动拉裂破坏为主。

(3)顺层岩体坡体的破坏主要以滑移破坏为主，并伴随有倾倒变形。在坡体发生滑动破坏时，上层块体下滑过程中的下滑力不足以抵消下层块体所带来的摩擦力时，动能传递至下层块体，从而产生了倾倒破坏。

(4)节理裂隙密度、走向和岩层倾角对边坡的稳定性影响较大，同一坡体中，节理裂隙密度越小，边坡越稳定；在内摩擦角相同时，岩层倾角越大越容易产生破坏变形，边坡越不稳定。

(5)DDA数值模拟很好地验证了物理模型试验中边坡失稳过程的变形规律，同时也验证了非连续变形理论分析方法的正确性和DDA软件的实用性。