基于多层次灰色评价模型的地下连续墙基础方案优选

张 祎

(西南科技大学 土木工程与建筑学院，四川 绵阳 621010)

1 引言

我国是基建大国，不仅是因为将铁路修到了青藏高原这种施工环境非常恶劣的地方，还因建成了很多高海拔的桥梁和建筑。其中，地下连续墙基础因其防水、承重性能良好普遍应用于这些建筑物中[1～4]。

在勘测阶段，有很多手段通过勘测工程的实际土壤性质和地形结构并结合经验来确定适合的地下连续墙基础类型。但往往会面对很多各方面性质差别不大的情况，此时经验的判断就显出不足，而多层次灰色评价模型就可以把定性的因素转化为定量的描述，通过更科学的手段来做出决策。

2 通过层次分析法建立指标体系

本文把地下连续墙基础方案优选过程看成是一个系统工程，把这个系统划为3个层次，有两级指标。其中一级指标主要考虑方案的可行性、施工质量、经济的适用性和对周边环境的影响4个因素，二级指标是从各个一级指标中细化的因素，比如隶属于方案可行性的二级指标包括地连墙基础的水平承载能力和结构稳定性2个指标，隶属于经济适用性的二级指标为材料用量和施工工期。建立好指标层次结构之后，再运用层次分析法对各项指标计算对应的权重。具体如表1所示。

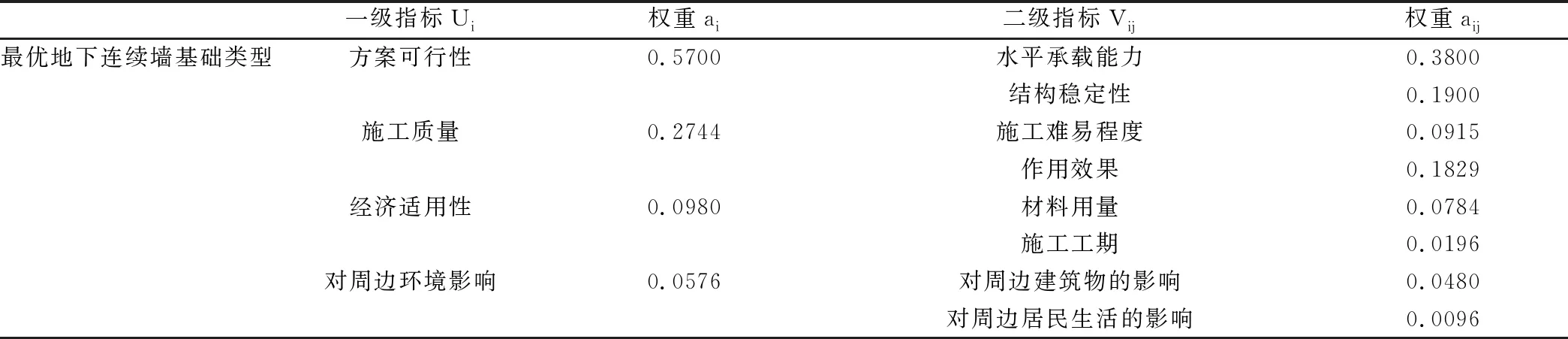
表1 地下连续墙基础方案优选的指标体系

3 多层次灰色评价模型

3.1 建立综合评价指标体系

假设评价对象的序号为s，W(s)代表第s个评价对象的综合评价值，U代表该系统的一级评价指标Ui组成的集合，Vij代表隶属于一级指标Ui的二级指标。利用层次分析法计算出各评价指标的权重，用ai和aij来表示。本文的结果如表1 所示。

3.2 制定二级评价指标的评分等级标准

这一步把各个定性指标转化为定量评价，以便于后续综合评价值的计算。把二级指标的优劣等级划分为四级，相应的赋值为4，3，2，1分，当二级指标的评价值介于两者之间时，可用3.5，2.5，1.5分来表示。

3.3 组织专家评分并得出评价矩阵

设评价专家的序号为k，共组织p个专家对第s个评价对象按照3.2的评分等级标准进行打分，由专家填写的专家评分表可得出第s个方案的评级矩阵。评价矩阵的元素用dijk(s)来表示。

3.4 确定评价灰类并计算灰色评价系数

根据二级指标的评价等级划分，设定4个评价灰类，灰类序号为e，即e=1，2，3，4。每个评价灰类对应的白化权函数fe如下：

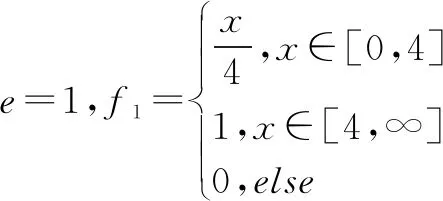
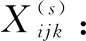
(1)

由灰色评价系数加和可以得到每个二级指标Vij属于所有灰类的总灰色评价系数：

(2)

3.5 计算灰色评价权向量和权矩阵

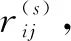
(3)

由上述的权向量，把属于同一个一级指标的二级指标的灰色评价权向量排列组合起来，就是对应一级指标的灰色评价权矩阵Ri(s)：

(4)

3.6 对Vi, U做综合评价

对第S个评价对象的Vi做综合评价，综合评价的结果记作Bi(s)，则综合评价的计算过程有：

Bi(s)=Ai·Ri(s)=(bi1(s)bi2(s)bi3(s)bi4(s))

(5)

式(5)中，Ai即为属于第i个一级指标的二级指标的权重向量，在计算过程中应进行归一化处理。

对Vi做完综合评价的结果Bi(s)得到整个项目U的总灰色评价矩阵为：

R(s)=[B1(s)B2(s)…Bn(s)]T

(6)

由总的灰色评价矩阵就可以对整个项目U做总的综合评价，结果记作B(s)：

B(s)=A·R(s)=(b1(s)b2(s)b3(s)b4(s))

(7)

3.7 计算方案的综合评价值并进行排序

由上可知，综合评价的结果是向量，向量无法对比，故应对其进行处理。根据前面设置的4种灰类，则有各评价灰类等级值化向量C=(4,3,2,1)。于是，有如下结果：

W(s)=B(s)·CT

(8)

这样就求得综合评价值W(s)，然后根据其大小对评价对象进行排序优选。

4 实际工程案例分析

4.1 工程概况

工程案例选取的是厦深高速铁路韩江中下游伍嘉陇特大桥，大桥起止里程为DK208+623.440～DK212+237.547，大桥全长3614.1 m、共 计110跨，上部为简支梁与连续梁结构[5]。该桥原设计采用群桩基础，但为了探究本方法的应用情况，拟另设计2种地连墙基础与群桩基础D(3)进行比较，分别为变截面井筒式地连墙基础D(1)和井筒式地连墙基础D(2)。下面以变截面地连墙基础为例表现多层次灰色评价法的应用。

4.2 制定评分等级标准

对本案例各二级指标的评分标准制定如表2。

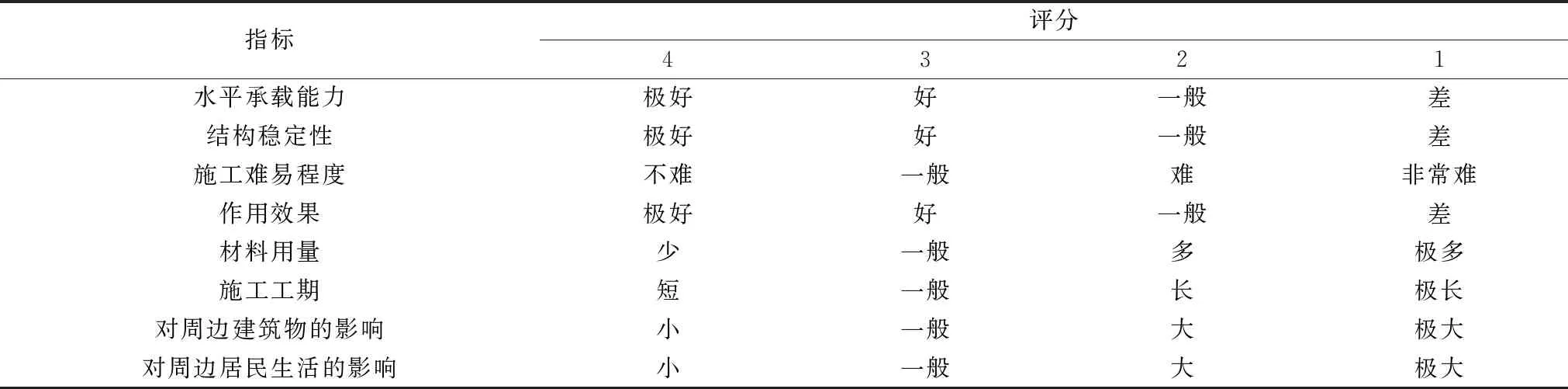
表2 地连墙基础二级指标的评分标准

4.3 组织专家评分并得出评价矩阵

根据4位专家的评分，可得到3个方案的评价矩阵，其中D(1)如下。

4.4 根据评价灰类计算灰色评价系数

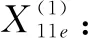
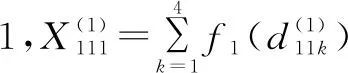
=f1(3)+f1(3.5)+f1(3)+f1(2.5)

=0.75+0.875+0.75+0.625=3

对各灰类的灰色评价系数进行加和，得到总的灰色评价系数为：

4.5 计算权向量、权矩阵并进行综合评价

由3.5可知，首先对单一灰色评价系数做归一化处理如下：

则V11的灰色评价权向量为：

同理可以得到剩余的7个二级指标的权向量，从而对属于同一个一级指标的二级指标的权向量进行组合，得到一级指标的灰色评价矩阵：

对一级指标进行综合评价，结果如下：

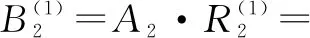
对综合评价结果进行组合得到变截面地连墙方案的总灰色评价矩阵：

对整个方案1进行综合评价如下：

B(1)=A·R(1)=[0.3436 0.4134 0.2324 0.0106]

计算综合评价值并排序，方案1变截面地连墙的综合评价值W(1)为：

W(1)=B(1)·CT

=3.0899

同理可以计算得出:方案2井筒式地连墙基础的综合评价值W(2)为：3.1366。方案3群桩基础的综合评价值W(3)为：3.0387。

5 结语

由第4节可知，W(2)>W(1)>W(3),这个案例的评选结果是方案2，即井筒式地连墙基础更适合于做这个大桥的基础。

本文通过层次分析法和灰色评价法相结合，建立了工程中地连墙基础方案优选的多层次灰色评价模型，对各方案的适宜性做出了定量并且科学的评价和判断。通过对实际工程的应用，可为其他类似工程的决策问题提供新的解决思路，当然，此方法可以应用于多种领域，具体还有待学者们探索。