常用排序算法的分析与比较

谢小玲，李山

（1.重庆市商务高级技工学校，重庆400067；2.林同棪（重庆）国际工程技术有限公司，重庆401123）

0 引言

当前正处于数据爆炸时代，云计算、大数据等热门领域都离不开数据分析，然而高效地数据分析是建立在有序序列的基础之上，因此研究排序方法具有重要意义。排序是指将一组数据按指定关键字的顺序进行排列的过程。按照排序过程是否需要将全部数据加载到内存中进行排序，可分为内部排序和外部排序[1]：其中内部排序是指将所有数据都加载到内存中进行排序；而外部排序是内外存结合的排序方法。由于内排序算法比较常用，所以本文选择研究主流的内排序算法。目前，许多研究者主要从理论去分析各种排序算法的执行效率[2-5]，其推导过程抽象难懂，得出的结论都是的渐进时间复杂度，相当于就是一个估算值，没有给出量化指标来指导选择何种排序算法。为此，本文选择了理论与编程试验相结合方式展开了研究，首先阐述了8 种排序算法的基本思路，定性地分析了它们的渐近时间复杂度，然后通过编程实验，定量地验算了不同的排序的时间效率。

1 排序算法简介

常用的内部排序算法可分为以下5 类（如图1 所示）：交换排序、插入排序、选择排序、归并排序和基数排序。

图1 常用排序算法分类

为了便于读者理解算法的思想，笔者采用举例说明：给定n 个数，要求按照递增排序。

1.1 交换排序

交换排序包括冒泡排序和快速排序。

（1）冒泡排序

冒泡排序的基本思想是对序列多趟从前往后依次比较相邻元素，如果发现逆序则交换它们的位置，其大概过程是：第1 趟遍历a1到an-1，依次比较ai和ai+1，若ai＞ai+1就交换ai和ai+1的位置；然后进入第2 趟遍历a1到an-2，仍依次比较ai和ai+1，若ai＞ai+1就交换ai和ai+1的位置；以此类推，当经过n-1 次遍历后，排序完成。该过程的每趟遍历都会得到一个较大值，就像水底冒泡一样，所以称之为冒泡排序。

（2）快速排序

快速排序算法是一种划分交换排序，其基本思想是：先从原序列中任选一个数ai，让ai与剩余的数相比较，把小于ai的数移到ai的左边，把大于ai大的数移到ai的右边，于是得到两个新的子序列，然后又对新的两个子序列采用上述步骤，直到新的子序列长度为1 时截止，此时整体序列排序完成。

1.2 插入排序

插入排序包括直接插入排序和希尔排序。

（1）直接插入排序

直接插入排序是对待排序列以插入方式找到适合位置的排序方法，其基本思路是：先把原序列分为有序子序列{a1}和无序子序列{a2，a3，…，an}，然后每轮循环从无序序列取出一个数ai插入到有序子序列合适的位置使之仍有序，经过n-1 轮循环后，排序完成。

（2）希尔排序

希尔排序是对直接插入排序算法的改进，它将待排序列中的元素下标按一定的步长进行分组，然后对每组数列按直接插入排序算法进行排序。其基本思路是：首轮排序设步长为h 且h＜n，把原序列分为多个子序列{a1，a1+h，a1+2h，…}，{a2，a2+h，a2+2h，…}，…，{ah-1，a2h-1，a3h-1，…}，然后分别对每一个子序列进行排序；接着进入第2 轮，把步长设为[h/2]，重新划分子序列并对其排序，以此类推，直到h=1 时，整体排序完成。

1.3 选择排序

选择排序包括简单选择排序和堆排序。

（1）简单选择排序

简单选择排序的基本思路是从原序列中选出最大元素ai，并交换ai和an的位置，此时an就是序列的最大值。接着从a1到an-1中选出新的最大值ai，再交换ai和an-1的位置，此an-1变为序列的次最大值，以此类推，经过n-1 次挑选，整体排序完成。

（2）堆排序

堆排序是一种利用完全二叉树进行排序的算法，假定使用大顶堆来排序，它的基本思路是先将原序列构成一个大顶堆，再把大顶堆的根结点ai和无序序列末尾元素an交换位置，由于交换位置后可能违反堆的性质，因此需要重新把a1到an-1构建一个大顶堆，再把堆顶元素ai与an-1交换；重复上述步骤，只需n-1 轮排序，便能得到一个有序序列。

1.4 归并排序

归并排序是采用经典的“分治策略”思想来进行排序，该算法的“分”很简单，就是把原序列看成n 个长度为1 的子序列，而“治”是先把n 个长度为1 的子序列合并为n/2 个长度2 为子序列，再把n/2 个长度为2 的子序列合并为n/4 个长度4 为子序列，重复上述步骤，直到所有数据合并1 个长度为n 的有序序列。

1.5 基数排序

基数排序的基本思想是将原序列的整数数位分割成不同的数字，数位较短的补零，从低位向高位进行排序，其大概过程是：先按个位上数字的大小进行第1 轮排序，得到一个新序列，再按十位上的数字大小对新的序列进行排序，以此类推，直到最高位排序完成后，整个序列就有序了。

2 排序算法复杂度分析

刻画算法的好坏主要是看它的时间复杂度T（n）和空间复杂度S（n），排序算法也不例外。时间复杂度是指算法执行时所耗费的总时长，空间复杂度是指算法执行时占用的内存空间单元长度，二者都是数据规模n 的函数。下面主要讨论常用排序算法的时间复杂度和空间复杂度。

2.1 时间复杂度

（1）冒泡排序

最坏情况下，若原序列是逆序，则需要n-1 轮遍历，第i 轮遍历需要比较n-i 次和交换n-i 次，此时最差时间复杂度为

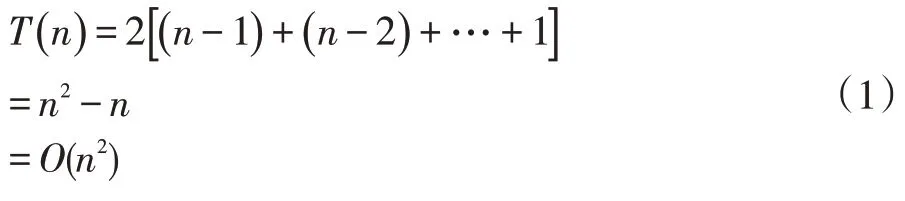
最好的情况下，若原序列本身有序，则只需要1 轮遍历就可以完成排序，该轮遍历只需比较n-1 次和交换0 次，所以最好时间复杂度为：

（2）快速排序

选取恰当的序列分割基准是快速排序的关键。最坏的情况下，如果每次选取的分割基准是当前无序序列的最大值（或最小值），将会得到空的左子序列（或右子序列），这时共需划分n-1 次才能排好序。在这递归过程中，第i 次划分需要比较n-i 次、交换n-i 次，所以最差时间复杂度为：

最好的情况下，每次选取的分割基准是当前区间的中值元素，划分结果是左右区间长度大致相等，此时只需logn 次递归，每次递归比较次数总和不超过n 次，所以最好的时间复杂度为O（nlogn）。

（3）直接插入排序

若原序列是正序时，则经过1 轮遍历便可完成排序，该次遍历的需比较n-1 次、交换0 次，最好的时间复杂度为：

若原始序列是逆序，则需要n-1 轮遍历，其中第i轮需比较n-i 次、交换n-i 次，所以最差时间复杂为：

（4）希尔排序

希尔排序的执行时间依赖于增量h 的选择，但目前h 的确定尚无较好的确定性理论，但Shell 建议较好的增量划分为hi=[n/2]，hi+1=[hi/2]，对应的最差时间复杂度为O（n2），最好时间复杂度为O（n）。

（5）简单选择排序

无论原序列的状态如何，简单选择排序都要进行n-1 轮遍历，且第i 轮遍历需n-i 次比较。另外，还要考虑每轮遍历的交换次数，当原序列是逆序时，则需要交换n-1 次；当原序列是正序时，需交换0 次，所以最差的时间复杂度为

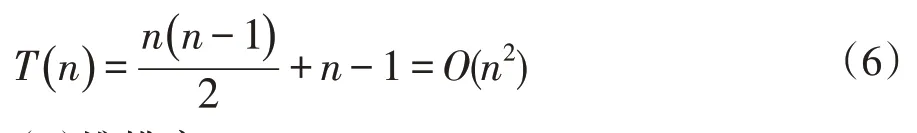
（6）堆排序

堆排序的时间主要耗费在构建初始堆和反复的重建堆上面，第一阶段构建初始堆最多比较2n 次，第二阶段需要重建堆n-1 次，第i 次最多比较logi 次，所以它的最坏时间复杂为O（nlogn）。

（7）归并排序

归并排序无论原序列状态如何，都要进行logn 次两路归并，每次合并比较次数不超过n，所以它的最差时间复杂度都为O（nlogn）。

（8）基数排序

设原序列中最大元素的数位为k，则基数排序需要k 趟排序，每趟排序最多需要比较n-1 次，所以它的最差时间复杂度为O（n*k）。

2.2 空间复杂度

上面讨论的8 种排序算法的空间复杂度都不超过O（nlogn）[5-6]：其中复杂度为O（1）的有冒泡排序、直接插入排序、希尔排序、简单选择排序、堆排序；复杂度为O（n）是归并排序；复杂度为O（n+k）是基数排序；复杂度为O（nlogn）是快速排序。

3 编程实验及结果分析

本次编程实验环境是Windows 10+内存16G，采用Java 语言分别对以上讨论的8 种排序算法进行了编程实现，并随机模拟了长度为103、104、105、106、107的数组，分别对每种长度的数组采用这8 种排序算法进行排序，其执行时间见表1。

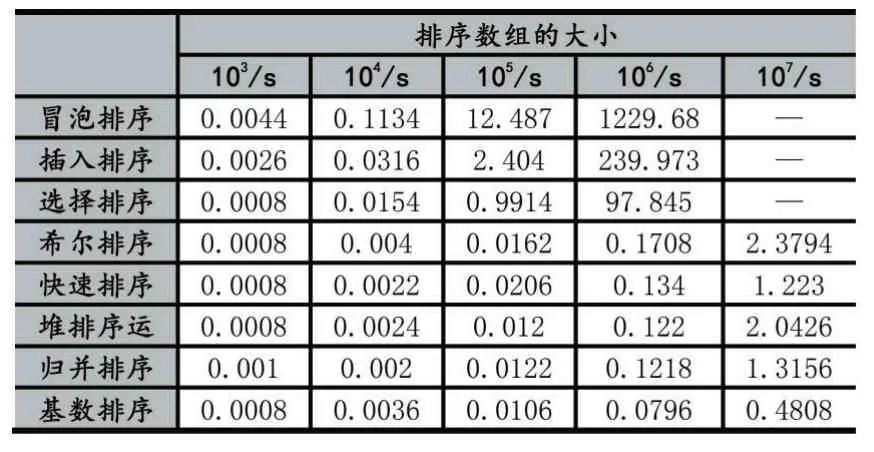
表1 不同排序算法的执行时间

从表1 可以看出，当待排数组的规模小于104时，各种排序算法的执行时间相差不大，都小于1 秒。但是待排数组的规模大于104时，冒泡排序、直接插入排序和简单选择排序随之耗费时间增加迅猛，特别是当数组的规模超过105时，它们的算法的执行时间让人难以等待，所以表1 中数组的规模达到107时，排序执行时间太长了，就没有列举出来了。

另外，让人惊喜的是即使数组的规模达到106时，希尔排序、快速排序、堆排序、归并排序和基数排序的执行时间不超过1 秒就完成了，甚至数组的规模达到107时，都在2 秒左右完成了，所以建议编程人员选择这几种排序方法。

4 结语

本文研究了8 种常用的排序算法，概述了各种排序算法的基本思想，分析了不同排序算法的时间复杂度和空间复杂度，并通过编程实验对各种排序算法的时间复杂度进行验算，对比了不同数组规模下排序执行时间，结果表明：算法的执行效率与理论分析相符合，当数组的规模小于104时，各种排序算法的执行时间都小于1 秒；但当数组的规模大于104时，应该选择执行时间较短的希尔排序、快速排序、堆排序、归并排序和基数排序，因为即使数组的规模达到107时，它们都能在2 秒左右完成。因此，这些量化的排序执行时间有利于选择合理的排序算法。