蠕变对河流侧蚀型黄土滑坡影响的数值模拟
2020-10-12张吉宏段钊唐皓
张吉宏 段钊 唐皓

摘 要:为了解蠕变对黄土斜坡变形破坏的影响,给河流侧蚀型黄土滑坡治理提供技术参考,对泾河下游舒唐王村一带塬边黄土进行蠕变试验,建立适用于该区黄土的自定义蠕变模型并进行数值模拟,分析蠕变效应对河流侧蚀型黄土滑坡变形破坏的影响,结果表明:蠕变对黄土滑坡变形破坏过程具有显著的促滑效应,蠕变效应显著加速了滑坡土体塑性区的发展及贯通,明显加剧了滑坡土体剪应变增量的放大与集中、增大了滑坡的水平位移。
关键词:黄土滑坡;蠕变效应;本构模型;河流侧蚀;数值模拟
中图分类号:S157.1;P642.22 文献标志码:A
doi:10.3969/j.issn.1000-1379.2020.02.030
Abstract:In order to understand the effect of creep on the deformation and failure of loess slope, and to provide technical reference for the treatment of loess landslide caused by river erosion, the creep test of loess in the loess plateau area of the downstream region of Jinghe River was carried out. A self-defined creep model suitable for the loess in this area was established and simulated with numerical method in this paper. It is concluded that the creep effect on the deformation and failure process of loess landslides is obvious, which accelerates the development and penetration of the plastic zone, and intensifies the enlargement and concentration of the shear strain increment in the soil, and the horizontal displacement of landslide is obviously increased.
Key words: loess landslide; creep effect; constitutive model; river erosion; numerical simulation
我國滑坡灾害以西部地区最为严重[1]。近年来黄土滑坡灾害的发生次数有逐年增加的趋势,对社会生产及群众生活构成了严重威胁,甚至引发重大灾难性后果[2],因此对黄土滑坡及其变形破坏规律的研究已成为一个热点。河流侧蚀型黄土滑坡具有厚度大、滑面深、潜伏期长、不易预警等特点,国内外众多学者[2-7]对其诱发机理、破坏模式等进行了研究,但研究中对蠕变的影响因素考虑较少。许多学者[8-14]将蠕变理论用于研究滑坡产生原因、变形规律等,并提出不同土的蠕变经验模型,但在黄土滑坡研究中的应用较少,黄土的蠕变特性对河流侧蚀黄土滑坡变形破坏规律的影响研究尚不够深入。陕西省泾河下游沿河分布有30多千米长的黄土台塬,受地貌影响及泾河不断侧蚀,在泾河南岸诱发了大量滑坡,笔者以目前该区仍在侵蚀过程中的舒唐王村一带塬边典型滑坡为例,分析其基于蠕变效应的变形破坏规律,以期为该类黄土滑坡治理提供技术参考。
1 黄土蠕变试验及特征分析
1.1 试验设计
蠕变试验设备为长春试验机研究所研制的CSS-2901TS型土体三轴流变试验机。试验黄土取自泾阳南塬舒唐王村滑坡坡脚,为Q2原状黄土,天然含水率为17%。三轴蠕变试验试样为圆柱形试样,尺寸为39.1 mm×80 mm。分别在50、100、150、200、250 kPa围压下对天然含水率试样及饱和试样进行不排水蠕变试验,蠕变试验采用单试件分级加载方法,设计强度以三轴压缩试验确定的峰值强度为依据[3],法向加载7级,单级加载时间为12 h。试验数据采用Boltzmann叠加原理进行处理。
1.2 应变—时间曲线分析
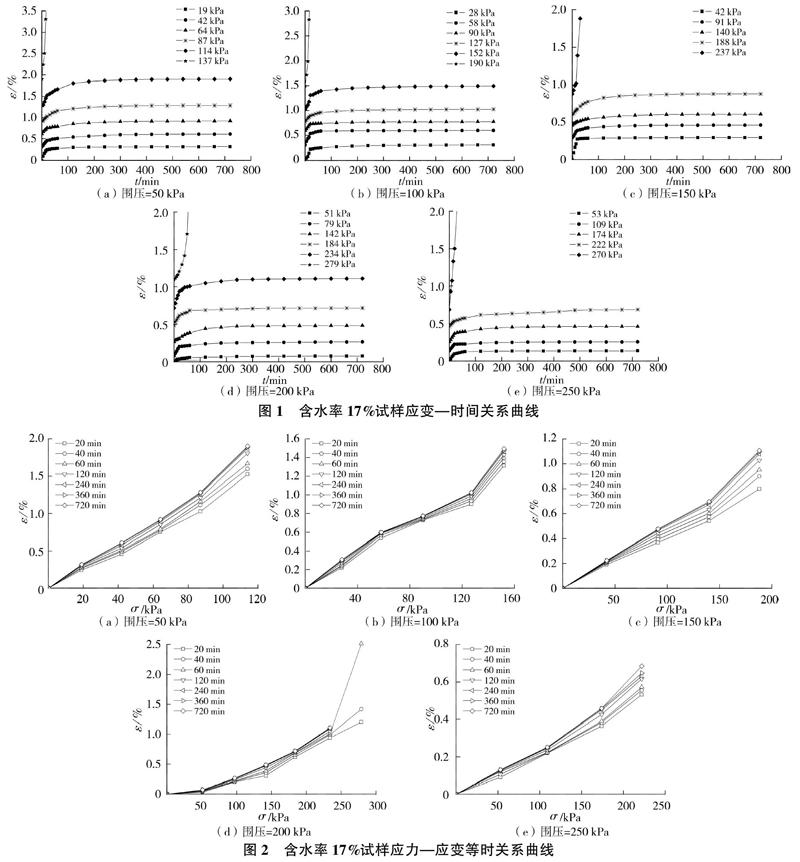
以含水率为17%的试样试验结果为例,不同围压及偏应力条件下的应变—时间关系曲线见图1(图中ε为应变、t为时间、各曲线代表不同偏应力状态),可以看出:试样在开始加载阶段的变形较快,在偏应力较小时以衰减蠕变为主,随着偏应力的逐渐加大出现等速蠕变直至加速蠕变;蠕变变形量随偏应力的增大而增加;围压越大,达到相同应变量所需要的偏应力更大,破坏应变也随之增大。饱和状态试样的试验结果与此类似,在此不再赘述。
1.3 应力—应变等时关系曲线分析
同样以含水率为17%的试样试验结果为例,其在不同围压下的应力—应变等时关系曲线见图2,可以看出试样的应力—应变等时关系曲线由直线段与曲线段组成,两者之间的转折点所对应的应力即为试样的屈服应力σs,当应力小于σs时试样主要表现为线性黏弹性特征,当应力大于σs时试样的非线性黏弹性特征表现得更为明显。饱和状态试样的试验结果与此类似,在此不再赘述。
2 黄土蠕变本构模型
2.1 本构模型的建立
由试验结果可以看出,研究区黄土蠕变变形呈现衰减稳定的特征,即由弹性变形和速率衰减的黏弹性变形共同组成蠕变变形,而Kelvin模型可以较好地描述这种变形。前已述及,研究区黄土蠕变变形在开始阶段增长较快,这与单一Kelvin模型蠕变曲线有一定的差异,因此为了加快蠕变初期变形增长速度,选用五元件广义Kelvin模型来描述,其由一个Hooke体和两个Kelvin体串联而成,如图3所示(图中:EH为Hooke体元件弹性模量,EK1、EK2为两个Kelvin体元件弹性模量,ηK1、ηK2为两个Kelvin体元件黏滞系数,五元件模型可表示为“H-(H/N)-(H/N)”,其中“-”表示串联、“/”表示并联、“H”为Hooke体、“H/N”为Kelvin体),应满足的应力应变条件见式(1)~式(5)。
式中:σ与ε分别为总应力与总应变;σ1与ε1分别为Hooke体应力与应变;σ2、σ3、ε2、ε3分别为两个Kelvin体的应力与应变。
当t=0(t为时间)时,ε=σ/EH,ε2=ε3=0,对式(1)~式(5)进行整理可得研究区黄土蠕变本构模型为
在式(6)的基础上,推广到三维状态下的蠕变本构模型差分形式为
式中:SNij、SOij分别为一个时间增量步内的新、老应力偏量;Δeij为应变增量;ΔePij为偏应变增量;eK1,Oij、eK2,Oij分别为两个Kelvin体在一个时间增量步内的老应变偏量;Ai=1+GKi2ηKiΔt,Bi=1-GKi2ηKiΔt,GKi、ηKi分别为Kelvin体的剪切模量与黏滞系数;a=12Ge+Δt4(1A1ηK1+1A2ηK2),b=12Ge-Δt4(1A1ηK1+1A2ηK2),Ge为Hooke体剪切模量,Δt为时间增量。
球应力的差分形式为
式中:σN0、σO0分别为一个时间增量步内的新、老球应力;K为体积模量;Δevol为体应变增量。
2.2 本构模型参数
得到蠕变本构模型后,选用ExpAssoc函数进行参数拟合,其函数形式为
将蠕变本构模型即式(6)展开,可得:
对比式(9)和式(10),可得:EH=σ/y0,EK1=σ/A1,EK2=σ/A2,ηK1=EK1t1=σt1/A1,ηK2=EK2t2=σt2/A2。
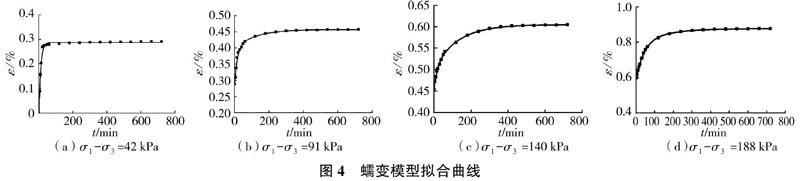
選用含水率w=17%的黄土试样、σ3=150 kPa的试验结果进行拟合,得到不同偏应力条件下本构模型参数值,见表1,拟合曲线见图4。由图4可以看出,试验数据与拟合曲线吻合度较高,说明该自定义本构模型能很好地描述研究区黄土的蠕变特征。
3 河流侧蚀型黄土滑坡变形破坏数值模拟
3.1 计算模型及参数
基于研究区滑坡的地层分布规律,将地层简化为饱和黄土、含水率为17%的非饱和黄土及饱和砂卵石3类,且仅考虑黄土地层的蠕变。为对比分析蠕变效应对斜坡变形破坏的影响规律,屈服准则分别采用Mohr-Coulomb模型及自定义蠕变模型。采用有限差分法软件FLAC3D进行数值模拟。
滑坡计算模型为左、右和底边界约束,地下水位位于斜坡顶面下9 m。设定侧蚀速率为每次1/3块即5 m,把3次连续向坡脚水平侧蚀15 m、综合计算不收敛、剪应变增量区或塑性区贯通作为滑坡变形破坏判别准则。考虑蠕变的数值模型中蠕变时间设定为1 a及5 a。计算模型见图5,模型参数见表2、表3。
3.2 蠕变效应对斜坡变形破坏的影响
(1)塑性区的影响。Mohr-Coulomb模型和自定义蠕变模型对斜坡塑性区数值模拟结果见图6,可以看出:在蠕变效应的影响下,土体塑性区的发展及贯通显著加速,在同一个侧蚀阶段,蠕变效应显著增大了土体塑性区范围,在斜坡塑性剪切带基本贯通、滑动即将发生时,蠕变效应的影响表现得更为明显。
(2)剪应变增量的影响。Mohr-Coulomb模型及自定义蠕变模型对斜坡剪应变增量的数值模拟结果见图7。可以看出,在蠕变作用下斜坡土体剪应变增量显著提高,并且在滑动面附近出现峰值聚集,尤其在斜坡坡脚处剪应变增量集中现象尤为明显,剪应变增量带也随之加宽。
(3)水平位移的影响。Mohr-Coulomb模型及自定义蠕变模型对斜坡水平位移数值模拟结果见图8。可以看出,考虑了蠕变效应的斜坡水平位移明显增大,在侧蚀初期(侧蚀1/3块),蠕变模型最大水平位移已经达到11 m,而未考虑蠕变的边坡位移仅3.6 m;随着蠕变作用的不断加强,到侧蚀末期(侧蚀3/3块)蠕变模型最大水平位移可达到112.8 m,而未考虑蠕变的边坡位移仅35.6 m。
综上所述,蠕变对黄土滑坡变形破坏过程具有显著的促滑效应,基于蠕变效应的斜坡稳定性明显降低。侧蚀发生之前斜坡土体应力平衡完成时在自重作用下已存在一定的蠕变变形,但此时土体应力水平较低,蠕变变形量相对较小,而侧蚀作用改变了斜坡的初始应力状态,斜坡需要重新分布应力场以形成新的应力平衡,在此过程中产生了新的蠕变变形,降低了斜坡的稳定性,可导致滑坡的发生。
4 结 论
对泾河下游舒唐王村一带塬边黄土进行蠕变试验及数值模拟,分析了蠕变对黄土斜坡变形破坏的影响,得到以下主要结论:根据蠕变试验的结果,自定义的五元件广义Kelvin蠕变模型能较好地描述研究区黄土的蠕变特性;蠕变效应显著加速了斜坡土体塑性区的发展及贯通,在同一个侧蚀阶段,蠕变效应显著增大了土体塑性区范围,这一特性在斜坡塑性剪切带基本贯通、滑动即将发生时表现得更为明显;考虑蠕变效应的斜坡土体剪应变增量的集中与放大明显加剧、水平位移明显增大,在侧蚀量相同的情况下,随着蠕变时间的延长,剪应变增量增大、剪应变增量带变宽、斜坡水平位移增大,这一点在侧蚀量增大的情况下表现得更为明显。
参考文献:
[1] 黄润秋.20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报,2007,26(3):433-454.
[2] 张茂省,李同录.黄土滑坡诱发因素及其形成机理研究[J].工程地质学报,2011,19(4):530-540.
[3] 段钊.黄土滑坡触发机理研究:以泾河下游南岸黄土塬区滑坡为例[D].西安:长安大学,2013:144-149.
[4] STEFANO Dapporto, MASSIMO Rinaldi, NICOLA Casagli. Failure Mechanisms and Pore Water Pressure Conditions: Analysis of a Riverbank Along the Arno River (Central Italy) [J]. Engineering Geology, 2001, 61: 221-242.
[5] 袁湘秦,赵法锁,段钊.河流作用诱发黄土滑坡机理[J].煤田地质与勘探,2018,46(4):154-160.
[6] 张常亮,王阿丹,邢鲜丽,等.侵蚀作用诱发黄土滑坡的机制研究[J].岩土力学,2012,33(5):1585-1592.
[7] 石菊松,李滨,吴树仁,等.宝鸡渭河北岸黄土塬边大型滑坡成因机制研究[J].工程地质学报,2013,21(6):938-949.
[8] 张先伟.结构性软土蠕变特性及扰动状态模型[D].长春:吉林大学,2010:205-207.
[9] 李曼,孙强.斜坡稳定性的流变模型分析[J].人民黄河,2009,31(9):112-113.
[10] 胡贵寿,李西宁,杨世新,等.黄南Ⅷ号滑坡变形破坏机制[J].人民黄河,2009,31(3):70-71.
[11] 葛苗苗,李宁,郑建国,等.基于一维固结试验的压实黄土蠕变模型[J].岩土力学,2015,36(11):3164-3170.
[12] 牛强.基于FLAC3D二次开发的黄土蠕变模型及滑坡失稳时间预测[D].兰州:兰州理工大学,2017:63-64.
[13] 张朝鹏.黄土的非线性流变本构模型及其在逆作法工程中的应用[D].西安:西安理工大学,2000:71-72.
[14] 颜斌,倪万魁,刘海松.公路黄土地基流变模型研究[J].中国公路学报,2009,22(4):15-19.
【责任编辑 张智民】
